Leetcode-1004. Max Consecutive Ones III

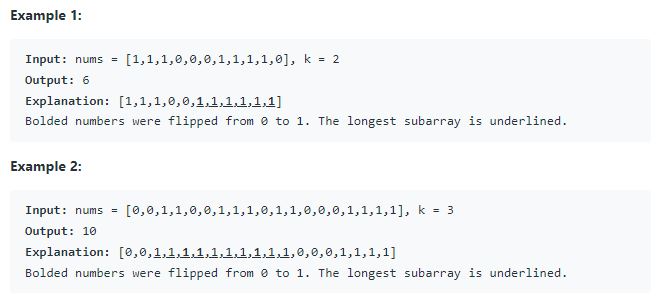
nums 배열이 주어지면 최대 k개의 0을 1로 뒤집을 수 있다고 하자.
이 때 어떤 인덱스의 0들을 1로 뒤집었을 때 연속된 1의 갯수가 가장 크게 나오는지 구해야 한다.

문제를 보고 완탐을 종종 떠올리는 내 고질병답게 모든 경우의 수를 다 체크해야하나..? 싶었다.
그러나 문제의 조건에서 nums.length가 최대 10^5 이기 때문에 완전 탐색은 무조건 시간 초과다.

결국 바로 다른 방법을 고민하였고 DP, 그리디, 이분 탐색 등과 같은 다양한 알고리즘들을 거쳐
투포인터, 슬라이딩 윈도우를 떠올렸다.

슬라이딩 윈도우는 고정된 크기의 윈도우를 움직이며 해당 범위 내의 요소들을 이용해 문제를 해결하는 것인데 우리가 고려해야할 크기는 가변적이다.
그렇기 때문에 나는 투포인터를 통해 접근하였다.

---

본 문제를 투포인터로 해결할 때 다음과 같은 조건을 구현해주면 된다.

( *start, end 두 개의 포인터가 존재한다 가정하자)

1. 현재 두 포인터 사이에 0의 갯수가 k개 이하이면 end를 +1 움직인다.

2. end가 움직이고 난 후 nums[end]의 요소가 0일 경우 0의 갯수를 카운트 +1 해준다.

3. 현재 두 포인터 사이에 0의 갯수가 k개 초과이면 start를 +1 움직인다.

4. 이때 start를 움직이기 전 nums[start]의 요소가 0일 경우 0의 갯수를 카운트 -1 해준다.

5. 두 포인터 사이에 0의 갯수가 k개 이하이면 1의 갯수를 늘 최댓값으로 갱신시켜준다.

😀😀

위 조건을 큰 토대로 작은 예외 사항들을 처리해주면 아래와 같이 문제를 해결할 수 있다.

• 정답 코드

class Solution:
    def longestOnes(self, nums: List[int], k: int) -> int:
        
        #투포인터
        start = 0
        end = 0
        count = 0 #포인터 내부에 0의 갯수 카운트
        one_count = 0 #start에서 end 까지 0 -> 1로 치환하고 내부 1의 총 갯수
        
        if len(nums) == 1: #길이가 1일때의 예외 처리
            if nums[0] == 0 and k == 0:
                return 0
            else:
                return 1
        
        if nums[start] == 0: #시작점이 0인지
            count += 1
        
        while end < len(nums): #end가 마지막 인덱스 도달할 때까지
            
            try: #인덱스 넘어가는 것 방지  
                if count <= k: #end가 더 나아가도 될 때
                    end += 1 #더 나아가고
                    if nums[end] == 0: #0인지 판단
                        count += 1
                        
                else: #count > k로 start가 나아가야 할 때
                    if nums[start] == 0: #0인지 먼저 판단하고
                        count -= 1
                    start += 1 #나아가기
                
                if count <= k:
                    one_count = max(one_count, end - start + 1)
                    
            except:
               break
            
        return one_count