백준 11049번
행렬 곱셈 순서, 동적 계획법
PYTHON
동적 계획법은 보통 dp 테이블을 작성하는 것으로 해답을 구한다.
간단한 문제들은 일차원 디피 테이블로 구할 수 있지만 이 문제는 이차원 디피 테이블을 이용해야 한다.
문제 해석
테이블을 시각화하면 아래와 같다.
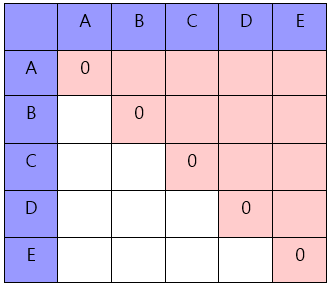
이 2차원 테이블에서 우리는 대각선을 기준으로 오른쪽 위만 사용한다.
이제 각 위치의 의미를 살펴본다.
(1, 2) 지점을 보면 (A, B)이다. 이 말은 A x B를 의미한다.
좀 더 자세히 살펴보면 (1, 3) 지점은 (A, C)로 A~C까지의 곱을 의미한다.
각 지점에는 최솟값만을 유지한다.
따라서 최종 목적은 (1, 5) => (A, E) 지점의 값을 구하는 것이다.
알고리즘
이제 이 값들을 구하는 방법을 살펴본다.
(A, D)를 생각해보면 아래의 계산 방법들이 존재한다.
A(BCD) = (A, A) + (B, D) + 마지막 행렬 곱셈
AB(CD) = (A, B) + (C, D) + 마지막 행렬 곱셈
ABC(D) = (A, C) + (D, D) + 마지막 행렬 곱셈
대각선 값은 자신으로부터 자기자신까지의 곱셈이므로 전부 0을 넣어준다.
소스 코드
가장 깊은 포문은 (A, D)로부터 나올 수 있는 모든 연산 과정을 검토하는 포문이다.
python3로는 시간초과가 되기 때문에 pypy3로 제출해야 통과할 수 있다.
Whiplash We Flash