[백준] 17298번 오큰수 - PYTHON

[백준] 17298번

오큰수

PYTHON

17298번 오큰수

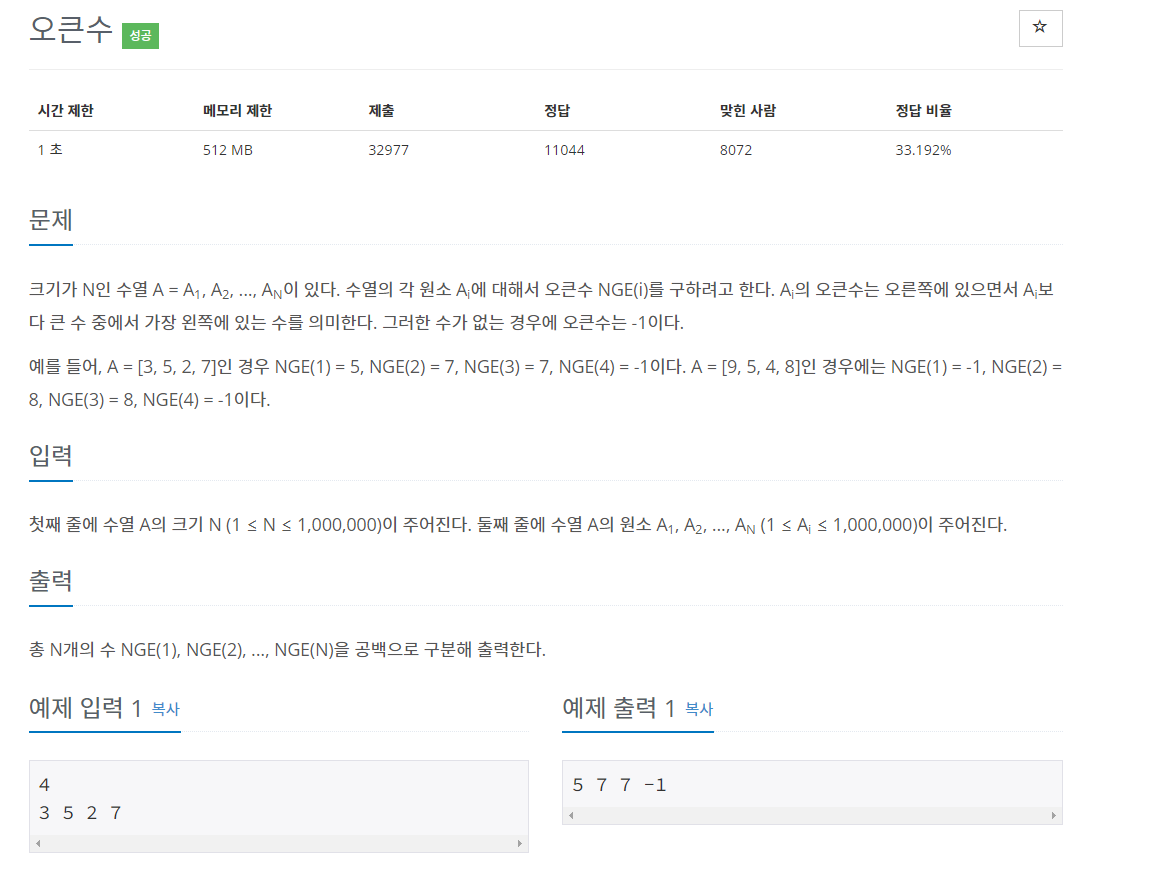
해당 문제에서 가장 중요한 조건은 시간 제한이다.

최대한 효율적인 방법으로 각 '인덱스'의 오큰수를 구해야 한다.

여기서 인덱스가 핵심이다.

처음에 문제를 접근할 때, 스택에 3, 5, 2, 7 처럼 인덱스가 아닌 실제 값을 삽입했었다.

그 경우에 스택에서 pop 연산을 수행했을 때, 해당 값의 인덱스를 다시 찾아야 했다. 따라서 리스트에 .index() 함수를 사용해야 했다.

이렇게 수행 했을 때, 시간 초과가 발생했다.

따라서 어차피 인덱스를 찾아야 하기 때문에 스택에 원소가 아닌 원소의 인덱스를 삽입하는 것으로 코드를 수정해서 해결할 수 있었다.

소스 코드를 살펴보자.

---

일단 정답 리스트를 모두 -1로 초기화한다. 이렇게 하는 이유는 밑에서 알 수 있다.

포문을 살펴보면

1. 스택이 비어있지 않거나.
2. 새로 읽은 값이 현재 스택 내부에 있는 값보다 큰 경우에

계속 해서 pop 연산을 하고 pop 된 인덱스에 현재 아이템 값을 넣어준다.

예를 들어,

3 5 2 7 의 경우에

처음에 스택에 3이 들어간다. [ 0 ]
이후에 5가 들어오면 3이 pop 된다. [ 1 ]
2가 들어오면 2는 5보다 작기 때문에 5가 pop 되지 않는다. [ 1, 2 ]
7이 들어오면 차례대로 모두 pop 된다. [ 3 ]

여기서 더이상 살펴볼 원소가 없기 떄문에 인덱스 3에는 오큰수를 삽입할 수 없다. 따라서 처음에 모든 값을 -1로 초기화해서 오큰수가 없는 경우에 -1 값을 유지하도록 한 것이다.

그리고는 NGE 리스트의 값을 전부 출력한다.