백준 2579번
계단 오르기
조건이 있는 동적 계획법이다.
우리가 할 수 있는 선택은
1) 한 계단 오르기 2) 두 계단 오르기이다.
이 때, 연속된 세 개의 계단을 밟을 수 없는 조건이 있다.
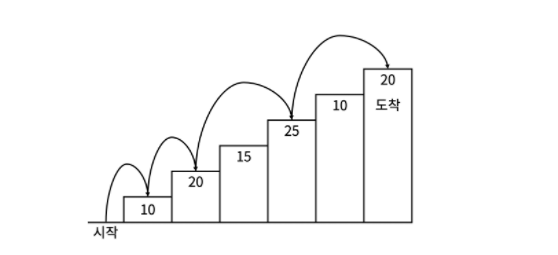
첫 번째, 두 번째, 세 번째 계단에 도달했을 때 얻을 수 있는
점수의 최댓값을 먼저 살펴보자.
첫 번째 계단의 경우 무조건 첫 번째 계단을 밟는 것이 최대이고
두 번째 계단 역시 첫 두 개의 계단을 모두 밟는 것이 최대이다.
세 번째 계단에서 변화가 생긴다.
문제에서 주어진 조건으로 세 개의 계단을 연속으로 밟을 수 없다고 했기 때문에
세 번째 계단 점수 = max(1번 + 3번, 2번 + 3번) 이다.
이 결과를 바탕으로 네 번째 계단을 살펴보자.
네 번째 계단은
- 1 + 2 + 4 의 계단을 밟는 경우
- 1 + 3 + 4 의 계단을 밟는 경우
이 두 가지의 경우 중에서 더 큰 값을 선택하게 된다. 이를 그림으로 살펴보면
이 결과를 점화식의 입장에서 생각해보자.
dp[i]를 i 번째 계단에서의 최대 점수 s[i]를 i 번째 계단의 점수 라고 하자
dp[4] = max(dp[1] + s[3] + s[4], dp[2] + s[4]) 로 표현할 수 있다.
이 식을 일반화하면 아래와 같다.
dp[i] = max(dp[i-3] + s[i-1] + s[i], dp[i-2] + s[i])
결과를 소스 코드로 확인하자.
Whiplash We Flash