DFS와 BFS

I. DFS (Depth-First Search, 깊이 우선 탐색)

1. 주요 개념

• Stack을 활용하여 구현한다.
• pop() 연산의 대상이 되는 노드가 방문하는 노드이다.

2. 탐색 예시

• [그래프]
  

---

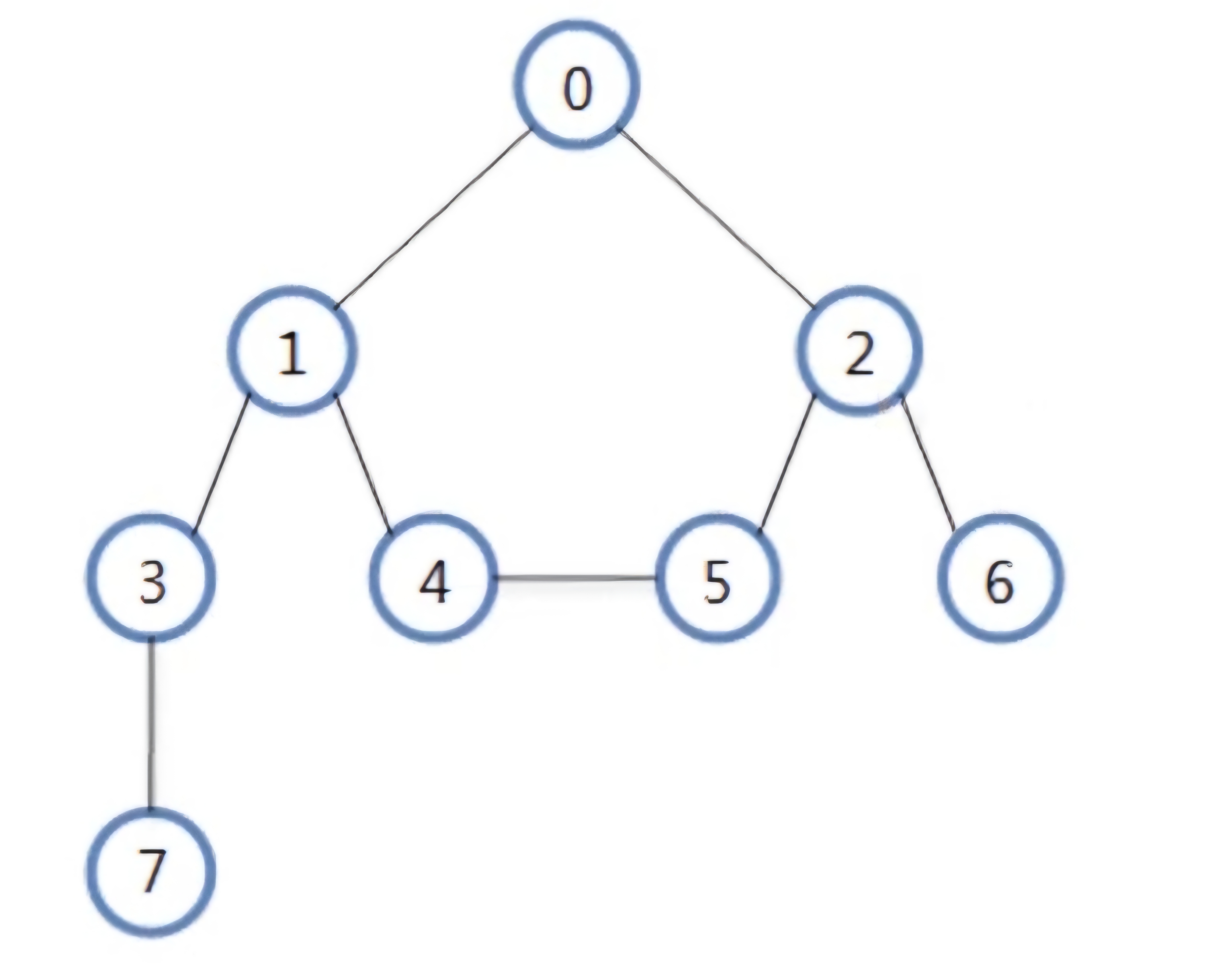
• 위의 그래프를 아래의 코드로 표현할 수 있다.
  [코드 1] UndirectedGraph.java

public class UndirectedGraph {
    private int count;
    private int[][] vertexMatrix;
    public UndirectedGraph(int count) {
        this.count = count;
        vertexMatrix = new int[count][count];
    }
    public void addEdges(int from, int to, int weight) {
        vertexMatrix[from][to] = weight;
        vertexMatrix[to][from] = weight;
    }
    public int[][] getMatrix() {
        return vertexMatrix;
    }
}

[코드 2] Main.java

public class Main {
    public static void main(String[] args) {
        int count = 8;
        UndirectedGraph graph = new UndirectedGraph(count);
        graph.addEdges(0, 1, 1);
        graph.addEdges(0, 2, 1);
        graph.addEdges(1, 3, 1);
        graph.addEdges(1, 4, 1);
        graph.addEdges(2, 5, 1);
        graph.addEdges(2, 6, 1);
        graph.addEdges(3, 7, 1);
        graph.addEdges(4, 5, 1);
    }
}

---

• 위의 그래프에서 DFS로 탐색할 경우 아래의 순서로 노드를 방문한다.
  • push(0)

    0

  • pop(0), push(1), push(2)

    1

    2

  • pop(2), push(5), push(6)

    1

    5

    6

  • pop(6)

    1

    5

  • pop(5), push(4)

    1

    4

  • pop(4)

    1

  • pop(1), push(3)

    3

  • pop(3), push(7)

    7

  • pop(7)

---

• pop()연산을 수행한 노드가 방문한 노드이므로, 아래와 같은 순서로 노드를 탐색한다.
  • 0 -> 2 -> 6 -> 5 -> 4 -> 1 -> 3 -> 7

II. DFS 구현 (in Java)

인접 행렬 이용

[코드 3] DfsAdjacentArray.java

import java.util.Stack;

public class DfsAdjacentArray {

    int count;
    boolean[] visited;
    Stack<Integer> stack;
    int[][] matrix;

    public DfsAdjacentArray(int count) {
        this.count = count;
        visited = new boolean[count];
        stack = new Stack<Integer>();
    }

    public void dfsTraversal() {

        stack.push(0);
        visited[0] = true;

        while (stack.size() != 0) {
            int node = stack.pop();
            System.out.print(node + "  ");

            for (int j = 0; j < count; j++) {
                if (matrix[node][j] != 0 && !visited[j]) {
                    stack.push(j);
                    visited[j] = true;
                }
            }
        }
    }
}

III. BFS (Breadth-First Search, 너비 우선 탐색)

1. 주요 개념

• Queue를 활용하여 구현한다.
• dequeue() 연산의 대상이 되는 노드가 방문하는 노드이다.

2. 탐색 예시

• [그래프]
  
• 위의 그래프에서 BFS로 탐색할 경우 아래의 순서로 노드를 방문한다.
  • enqueue(0)

    0

  • dequeue(0), enqueue(1), enqueue(2)

    1

    2

  • dequeue(1), enqueue(3), enqueue(4)

    2

    3

    4

  • dequeue(2), enqueue(5), enqueue(6)

    3

    4

    5

    6

  • dequeue(3), enqueue(7)

    4

    5

    6

    7

  • dequeue(4), dequeue(5), dequeue(6), dequeue(7)

---

• dequeue()연산을 수행한 노드가 방문한 노드이므로, 아래와 같은 순서로 노드를 탐색한다.
  • 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7

IV. BFS 구현 (in Java)

인접 행렬 이용

[코드 4] DfsAdjacentArray.java

import java.util.Stack;

public class DfsAdjacentArray {

    int count;
    boolean[] visited;
    Stack<Integer> stack;
    int[][] matrix;

    public DfsAdjacentArray(int count) {
        this.count = count;
        visited = new boolean[count];
        stack = new Stack<Integer>();
    }

    public void dfsTraversal() {

        stack.push(0);
        visited[0] = true;

        while (stack.size() != 0) {
            int node = stack.pop();
            System.out.print(node + "  ");

            for (int j = 0; j < count; j++) {
                if (matrix[node][j] != 0 && !visited[j]) {
                    stack.push(j);
                    visited[j] = true;
                }
            }
        }
    }
}

V. 실행

1. 실행 전 코드

[코드 5] Main.java

public class UndirectedGraph {

    private int count;
    private int[][] vertexMatrix;

    public UndirectedGraph(int count) {
        this.count = count;
        vertexMatrix = new int[count][count];
    }

    public void addEdges(int from, int to, int weight) {
        vertexMatrix[from][to] = weight;
        vertexMatrix[to][from] = weight;
    }

    public int[][] getMatrix() {
        return vertexMatrix;
    }
}

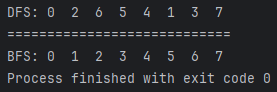
2. 실행 결과

• 위의 탐색 예시에서 언급한 방문 순서와 동일한 것을 확인할 수 있다.