알고리즘 #0005

• 문제 링크: 바로가기 (클릭)

I. 문제 상황

1. 초기 코드 작성

• 주어진 문제에 따르면, 1칸과 2칸을 배합할 수 있는 모든 경우의 수를 구해야 한다.
• 먼저 아래의 [코드 1]처럼 코드를 작성한다.
• nCr = $n!\over(n-r)!$인 점에 착안하여 조합을 구하는 메서드를 정의하였다.
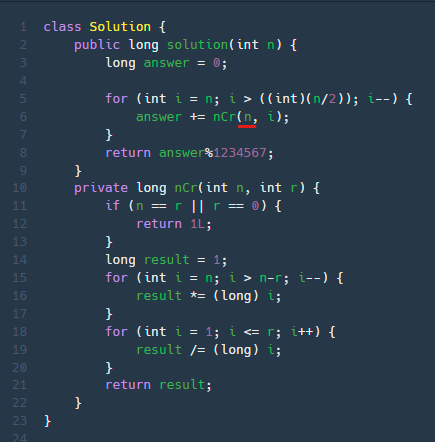
• [코드 1] 처음 작성한 코드 답안

class Solution {
    public long solution(int n) {
        long answer = 0;
        for (int i = n; i > ((int)(n/2)); i--) {
            answer += nCr(n, i);
        }
        return answer%1234567;
    }
    private long nCr(int n, int r) {
        if (n == r || r == 0) {
            return 1L;
        }
        long result = 1;
        for (int i = n; i > n-r; i--) {
            result *= (long) i; 
        }
        for (int i = 1; i <= r; i++) {
            result /= (long) i;
        }
        return result;
    }
}

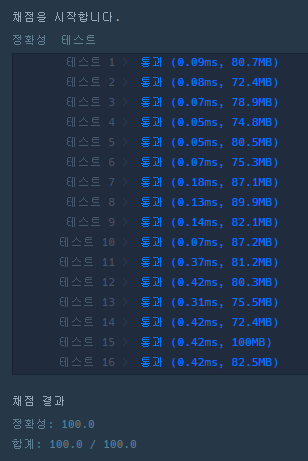
2. 실행 결과

• 하지만, 아래의 [결과 1]에서처럼 오류가 발생하였다.
• [결과 1]
  

II. 문제 분석

1. 디버깅

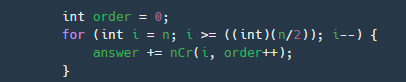
• 기존 [코드 1]에서, nCr 연산을 수행할 때 n 값이 항상 일정하다는 문제가 있는 것 같다.
• [코드 1] - 문제가 될 것으로 추청되는 코드 (강조)
  

---

• 따라서 [코드 2]와 같이 반복문을 수정하였다.
• [코드 2] 수정한 코드
  

2. 실행

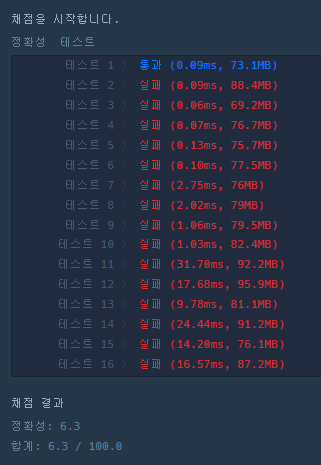
• [결과 2]
  

---

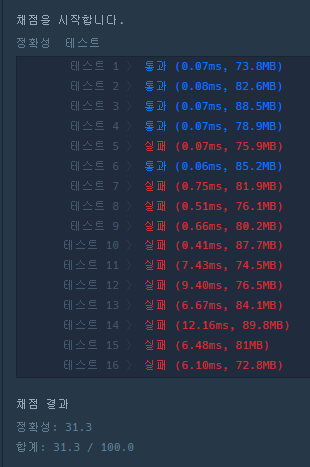
• 정답인 테스트 케이스가 늘었지만 아직도 오답인 경우가 발생한다.

3. 테스트 케이스 분석

• 결과적으로 n이 1일 때부터 모든 경우의 수를 계산한 결과 피보나치 수열과 동일한 값이 나온다는 결론에 이르렀다.
• 따라서 아래와 같이 코드를 수정하였다.
• [코드 3]

class Solution {
    public long solution(int n) {
        return fibonacci(n, 0L, 1L)%1234567;
    }
    private long fibonacci(int n, long a, long b) {
        long sum = a + b;
        if (n <= 1) {
            return sum%1234567;
        }
        sum = fibonacci(n-1,b, sum%1234567);
        return sum%1234567;
    }
}

4. 결과

• [결과 3]