Network Layer

---

라우팅 프로토콜의 목적

: 송신 호스트부터 수신 호스트까지 네트워크의 라우터를 통하는 "좋은" 경로를 결정하는 것.

경로: 패킷이 지나는 라우터의 순서

그래프

• G = (N, E)

• N = 라우터의 집합

• E = 이음선의 집합

• c(x, x') = 이음선(x, x')의 비용

u와 z 사이에 최소 비용 경로에 대해 라우팅 알고리즘을 통해 찾는다.

라우팅 알고리즘의 분류

1. 정보(Global vs Decentralized)

   Global:

   • 모든 라우터가 비용과 관련한 정보를 알고 있음
   • "link state" 알고리즘

   Decentralized:

   • 라우터는 근처에 연결된 라우터의 비용만 알고 있음
   • 계산의 반복 프로세스, 이웃과의 정보 교환
   • "distance vector" 알고리즘

2. 정적(static) vs 동적(static)

   static:

   • 경로는 매우 느리게 변한다

   dynamic:

   • 경로가 매우 빠르게 변한다

     • 주기적으로 업데이트
     • 비용 변할 때, 반응

---

link-state 알고리즘

다익스트라 알고리즘!

• 모든 노드에 경로와 그 비용이 알려져 있다.
• 한 출발지 노드에서 모든 다른 노드로의 최소 비용 경로를 계산
• 반복 횟수: k번 반복할 시, 최소 k개의 목적지에 대한 최소 경로를 지닌다.

용어 정리

• c(x,y): 노드 x부터 y까지의 링크 비용
  단, 연결되지 않을 시 INF로 지정.
• D(v): 출발지에서 목적지 v까지의 현재 비용
• p(v): 출발지에서 목적지 v로의 경로를 따른 이전 노드
• N': 최소 비용 경로가 명확하게 알려진 노드 집합

예제 1

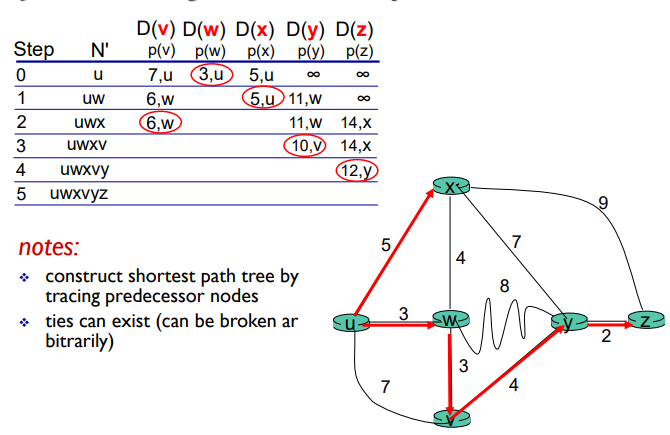
예제 2

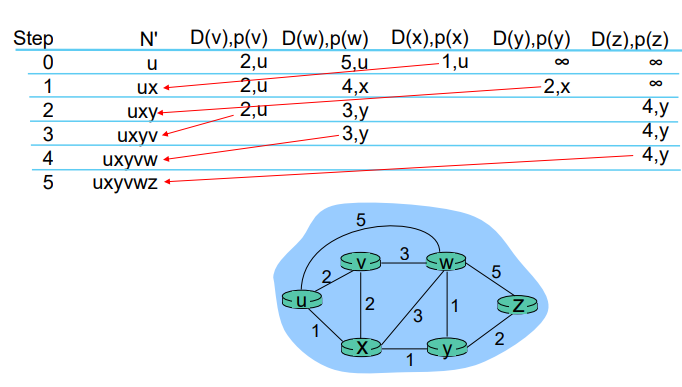
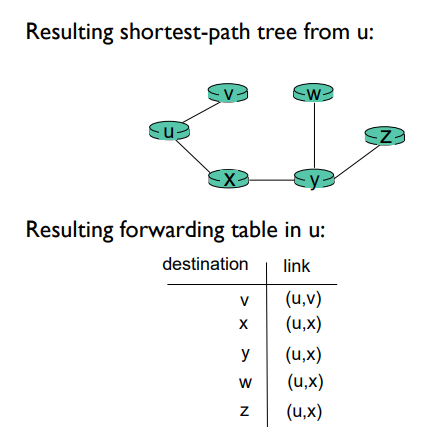
추가 정보

알고리즘의 시간 복잡도: O(n^2)
-> O(nlogn)까지 향상 가능.

진동이 가능하다.

---

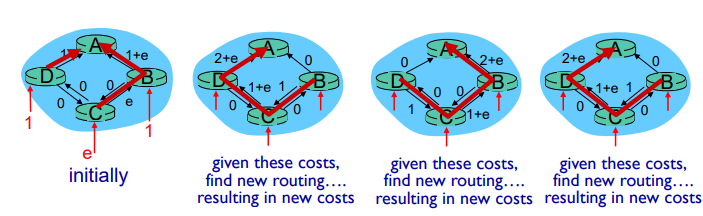
Distance vector 알고리즘

Bellman-Ford 방정식

작동 방식

node x:

• 각 이웃으로의 비용에 대해 알고있다
• 이웃의 거리 벡터를 유지

핵심 아이디어:

• 때때로, 각 노드는 자신의 거리 벡터 추정치를 이웃에게 보냅니다.
• x가 인접 네트워크로부터 새 DV 추정치를 수신하면 B-F를 사용하여 자체 DV를 업데이트합니다.

  방정식:
  

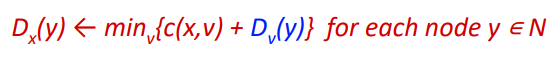
사소한 자연 조건 하에서 추정 𝐷(𝑦)는 실제 최소 비용 𝑑(𝑦)으로 수렴!

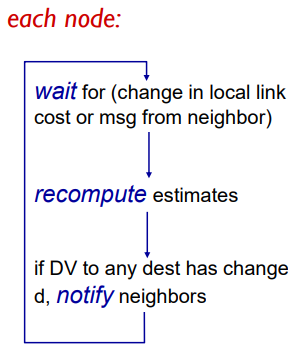
반복, 비동기: 각 로컬 반복은 다음과 같이 발생합니다.

• 지역 링크 비용의 변화
• 인접 네트워크의 DV 업데이트 메시지

분산:

• 각 노드는 노드의 DV가 변경되었을 때만, 이웃에게 알린다.
• 이웃들은 그들의 이웃에게 필요할경우 알린다.

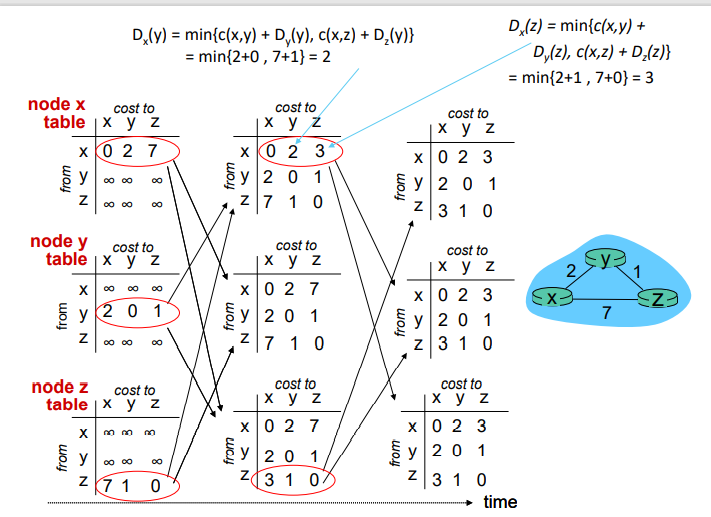
예제 1

링크 비용 변화

• 노드는 지역 링크 비용의 변화를 감지한다.
• 라우팅 정보를 업데이트하고, DV를 재계산한다.
• DV가 변할경우, 주위에 알린다.

좋은 뉴스는 빨리 퍼진다

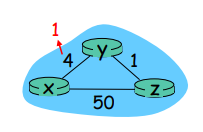
나쁜 뉴스는 느리게 퍼진다.

count to infinity 문제

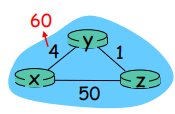
해결방안

poisoned reverse 방식!

만약 Z가 Y를 지나 X로 간다고 하자.
Z -> Y -> X
이때, Z는 Y에게 Z에서 X로 가는 비용이 무한하다고 알린다.

하지만 이 방식또한 완전하게 해결하는 것은 아니다.

LS와 DV 알고리즘의 비교

메시지 복잡성

• LS: N개의 노드, E개의 이음선, O(N*E) 메시지를 보낸다.
• DV: 이웃끼리만 교환한다.

수렴 속도

• LS: O(N^2) 알고리즘은 O(N*E)개의 메시지가 필요하다

  진동을 가질 수도 있다.

• DV: 수렴 시간은 달라진다.

  • routing loops가 있을 수 있다.
  • count-to-infinity 문제

견고성: 라우터가 오작동하면 어떻게 됩니까?

• LS:

  • 노드는 잘못된 비용을 광고한다.
  • 각 노드는 각자의 테이블만 계산한다.

• DV:

  • 노드는 잘못된 경로 비용을 광고한다.
  • 각 노드의 테이블은 다른 노드들에 의해서 사용된다.
  • 오류가 네트워크를 통해 전파됨