[백준] S3 1929번 소수 구하기 (Java)

https://www.acmicpc.net/problem/1929

해당 문제는 'Do it! 알고리즘 코딩테스트 자바 편'을 보면서 공부한 내용입니다.

👉 문제

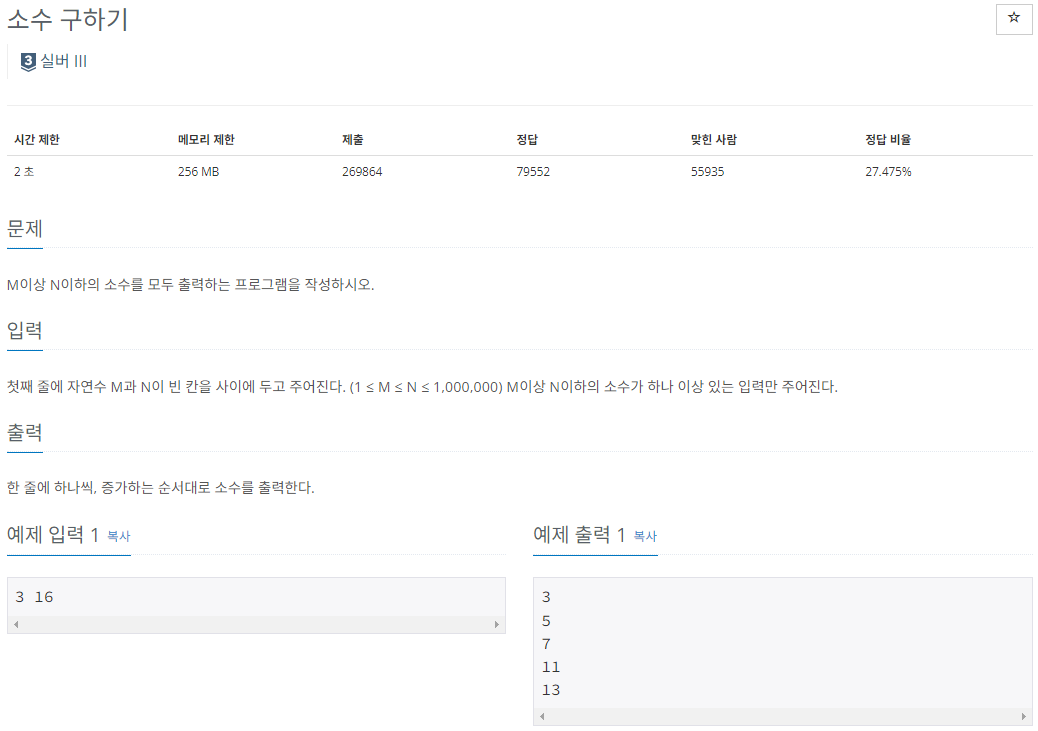
N의 최대 범위가 1,000,000 이므로 일반적인 소수 구하기 방식으로 문제를 풀면 시간 초과가 발생합니다. 따라서 에라토스테네스 라고 하는 방법으로 문제를 풀어야 한다고 합니다..

에라토스테네스의 체 원리
1. 구하고자 하는 소수의 범위만큼 1차원 배열을 생성합니다.
2. 2부터 시작하고 현재 숫자가 지워지지 않을 때는 현재 선택된 숫자의 배수에 해당하는 수를 배열에서 끝까지 탐색하면서 지웁니다. 이때 처음으로 선택된 숫자는 지우지 않습니다.
3. 배열의 끝까지 2를 반복한 후 배열에서 남아 있는 모든 수를 출력합니다.

1. 크기가 N+1인 배열을 선언한 후 값은 각각의 인덱스 값으로 채웁니다.

2. 1은 소수가 아니므로 굳이 값을 배정하지 않고, 2부터 시작합니다.

3. 2부터 N의 제곱근까지 값을 탐색합니다. 값이 인덱스값이면 그대로 두고, 그 값의 배수를 탐색해 0으로 변경합니다.

   N의 제곱근까지만 탐색하는 이유
   --------------------------
   N이 a*b라고 가정했을 때, a와 b 모두 N의 제곱근보다 클 수 없습니다. 따라서 N의 제곱
   근까지만 확인해도 전체 범위의 소수를 판별할 수 있습니다. 만약 16의 범위까지 소수를 
   구할 때 16 = 4 * 4로 이뤄지면 16보다 작은 숫자는 항상 4보다 작은 약수를 갖게 된다
   는 뜻이 됩니다. 따라서 4까지만 확인하고 소수 판별을 진행하면 됩니다.

4. 배열에 남아 있는 수 중 M이상 N이하의 수를 모두 출력합니다.

👉 풀이

import java.util.Scanner;

public class P1929_소수구하기_1 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int M = sc.nextInt();
        int N = sc.nextInt();
        int[] arr = new int[N + 1];
        for (int i = 2; i <= N; i++) {
            arr[i] = i;
        }

        for (int i = 2; i <= Math.sqrt(N); i++) {  // 제곱근까지만 수행
            if (arr[i] == 0) {
                continue;
            }

            for (int j = i + i; j <= N; j = j + i) {    // 배수 지우기
                arr[j] = 0;
            }
        }

        for (int i = M; i <= N; i++) {
            if (arr[i] != 0) {
                System.out.println(arr[i]);
            }
        }
    }
}

👉 성능