이 글은 멋쟁이 사자처럼 부트캠프 회고팀 내에서 세미나처럼 각자 원하는 주제를 맡아 발표한 것을 글로써 기록한 것입니다.
🤔 알고리즘이란?
- 어떤 문제를 해결하기 위한 동작들의 절차
- 일상에서의 예시로 내가 어떤 목적지까지 가기까지의 과정
- 프로그래밍에서는 입력 받은 Input을 통해서 원하는 Output을 얻는 과정
정렬 알고리즘
- '데이터'를 '특정한 기준에 따라 순서대로 정렬'하는 알고리즘을 의미
- 이때, 주어진 문제를 해결하기 위한 최선의 알고리즘을 선택해야 한다.
- 고려해야 할 사항 : 시간 복잡도 & 공간 복잡도
- 시간 복잡도 : 알고리즘이 실행될 때 필요한
입력 값과연산 수행 시간에 따라 효율적인 알고리즘을 나타내는 척도 - 공간 복잡도 : 알고리즘이 실행될 때 필요한
메모리 공간의 양
보통 코딩 테스트 문제에서는 메모리 제한이 여유로운 편이기 때문에 공간 복잡도까지 생각한 적은 많이 없었던 것 같다. 그러니 우선은 시간 복잡도에 대해서만 간단하게 살펴보고 가자.
나중에 여유가 된다면 공간 복잡도에 대해서도 다뤄봐야겠다.
시간 복잡도
컴퓨터 과학에서 알고리즘의 시간복잡도는 입력을 나타내는 문자열 길이의 함수로서 작동하는 알고리즘을 취해 시간을 정량화하는 것이다.
말 그대로 입력에 비해 시간이 얼마나, 연산이 얼마만큼 수행되는가를 나타낸 수치이다.
알고리즘의 시간복잡도는 주로 빅-오 표기법을 사용하여 나타내는데,
빅오 표기법(Big-O notation)
- 복잡도를 나타내는 점근 표기법 중 가장 많이 사용되는 표기법
- 가장 많이 사용되는 이유는 알고리즘의 효율성을 흔히 상한선을 기준으로 표기하기 때문
- 즉, 최악의 경우를 고려하는 데 가장 좋은 표기법이다.
최악의 경우를 분석함으로써 알고리즘을 설계할 때 성능을 예측하고 어느 정도의 실행 속도를 보장할 수 있는지를 확인할 수 있다는 뜻이다.
혹시 자세한 설명이 필요하다면 아래의 블로그를 참조하면 좋을 것 같다.
<시간 복잡도 설명이 잘 나와있는 블로그>
퀵 정렬과 분할 정렬의 시간 복잡도는 다음과 같다.
| 종류 | 최선 시간 복잡도 | 평균 시간 복잡도 | 최악 시간 복잡도 |
|---|---|---|---|
| 퀵 정렬 | O(NlogN) | O(NlogN) | O(N²) |
| 병합 정렬 | O(NlogN) | O(NlogN) | O(NlogN) |
분할 정복(Divide and Conquer)
- 여러 알고리즘의 기본이 되는 해결 방법으로, 큰 문제를 작은 문제로 나누어서 해결하는 알고리즘이다.
- 분할 -> 정복 -> 결합 의 세 단계의 구조를 가진다.
- 분할 : 문제를 작은 부분 문제들로 나누고
- 정복 : 부분 문제를 해결 및 정복하고
- 결합 : 부분 문제의 해들을 모아 본래 구하고자 하는 해를 구한다.
퀵 정렬과 병합 정렬이 이 분할과 정복 방법이 사용되는 대표적인 예시이다.
🔎 퀵 정렬 (Quick Sort)
- 분할 정복(Divide and Conquer) 방법을 사용하여 구현된 정렬 알고리즘
- 대규모 데이터를 정렬하는 데 매우 유용하며, 많은 프로그래밍 언어에서도 내장된 정렬 함수에 사용되는 알고리즘
동작방식
1. 피벗을 하나 선택한다.
2. 피벗을 기준으로 양쪽에서 피벗보다 큰 값, 혹은 작은 값을 찾는다.
왼쪽에서부터는 피벗보다 큰 값을 찾고, 오른쪽에서부터는 피벗보다 작은 값을 찾는다.
3. 양 방향에서 찾은 두 원소를 교환한다.
4. 왼쪽에서 탐색하는 위치와 오른쪽에서 탐색하는 위치가 엇갈리지 않을 때 까지
2번으로 돌아가 위과정을 반복한다.
5. 엇갈린 기점을 기준으로 두 개의 부분리스트로 나누어 1번으로 돌아가
해당 부분리스트의 길이가 1이 아닐 때 까지 1번 과정을 반복한다. (Divide : 분할)
6. 인접한 부분리스트끼리 합친다. (Conqure : 정복)이때, 피벗을 선택하는 과정은 여러 방법이 있다. 부분 배열에서
- 가장 왼쪽 원소가 피벗이 되는 방법
- 중간 원소가 피벗이 되는 방법
- 마지막 원소가 피벗이 되는 방법
-> 이해하기 가장 쉬우면서 기본적인 방법 = 왼쪽 피벗 선택 방식
아래의 그림을 보면서 동작 과정을 이해해보자.
그림은 알고리즘 공부할 때마다 큰 도움이 되는 https://st-lab.tistory.com/ 선생님의 블로그에서 가져오게 되었다..
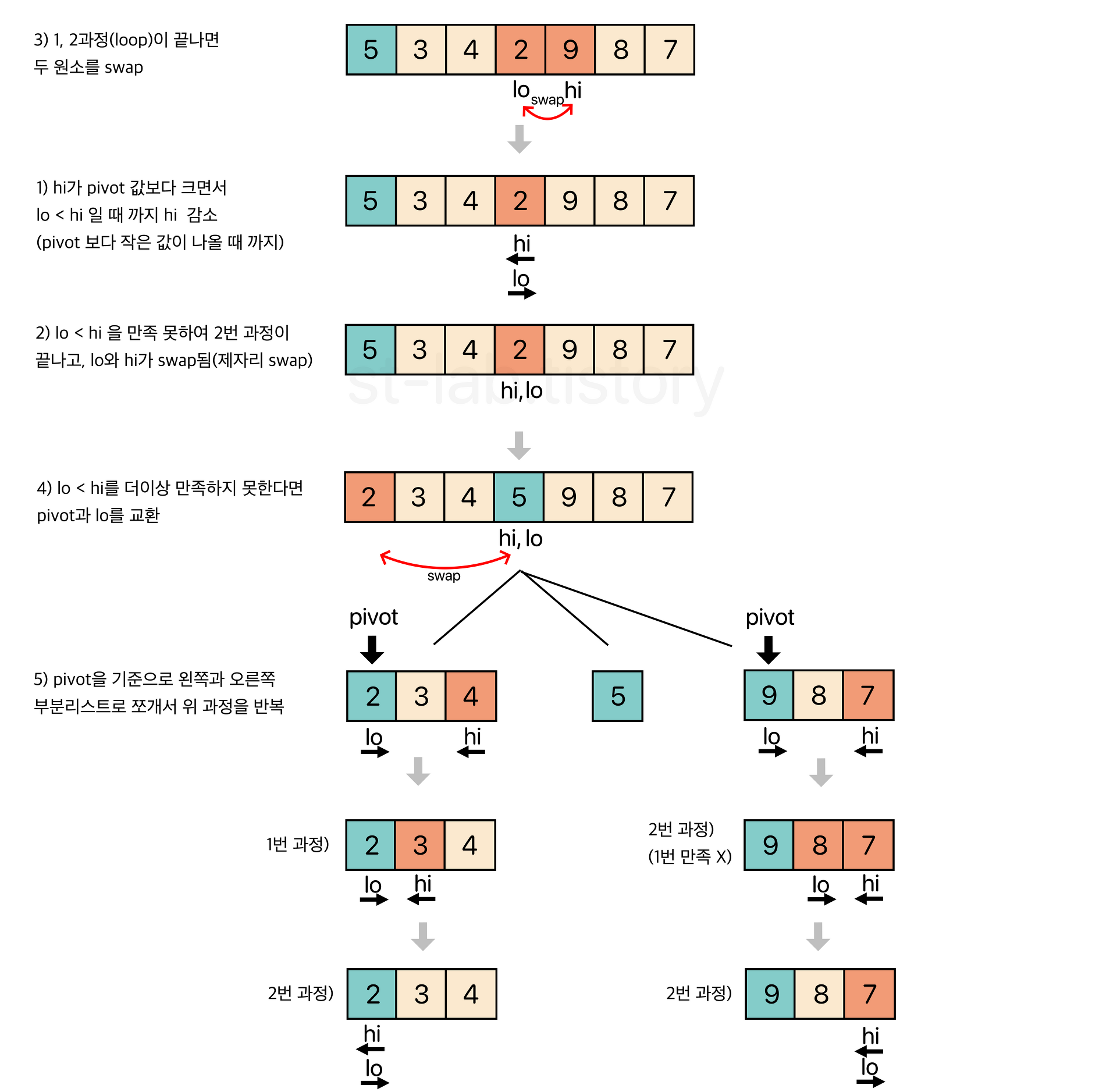
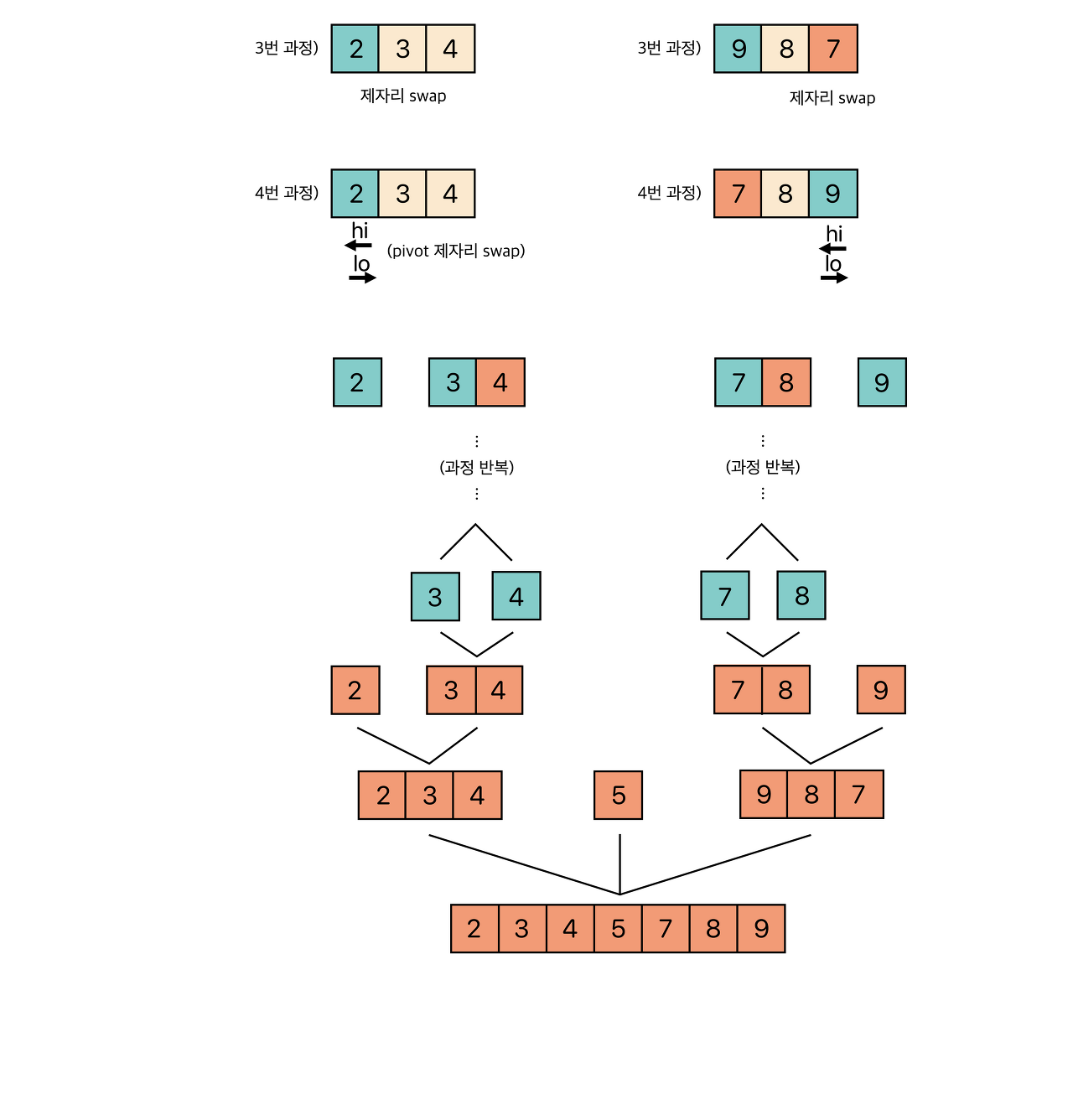
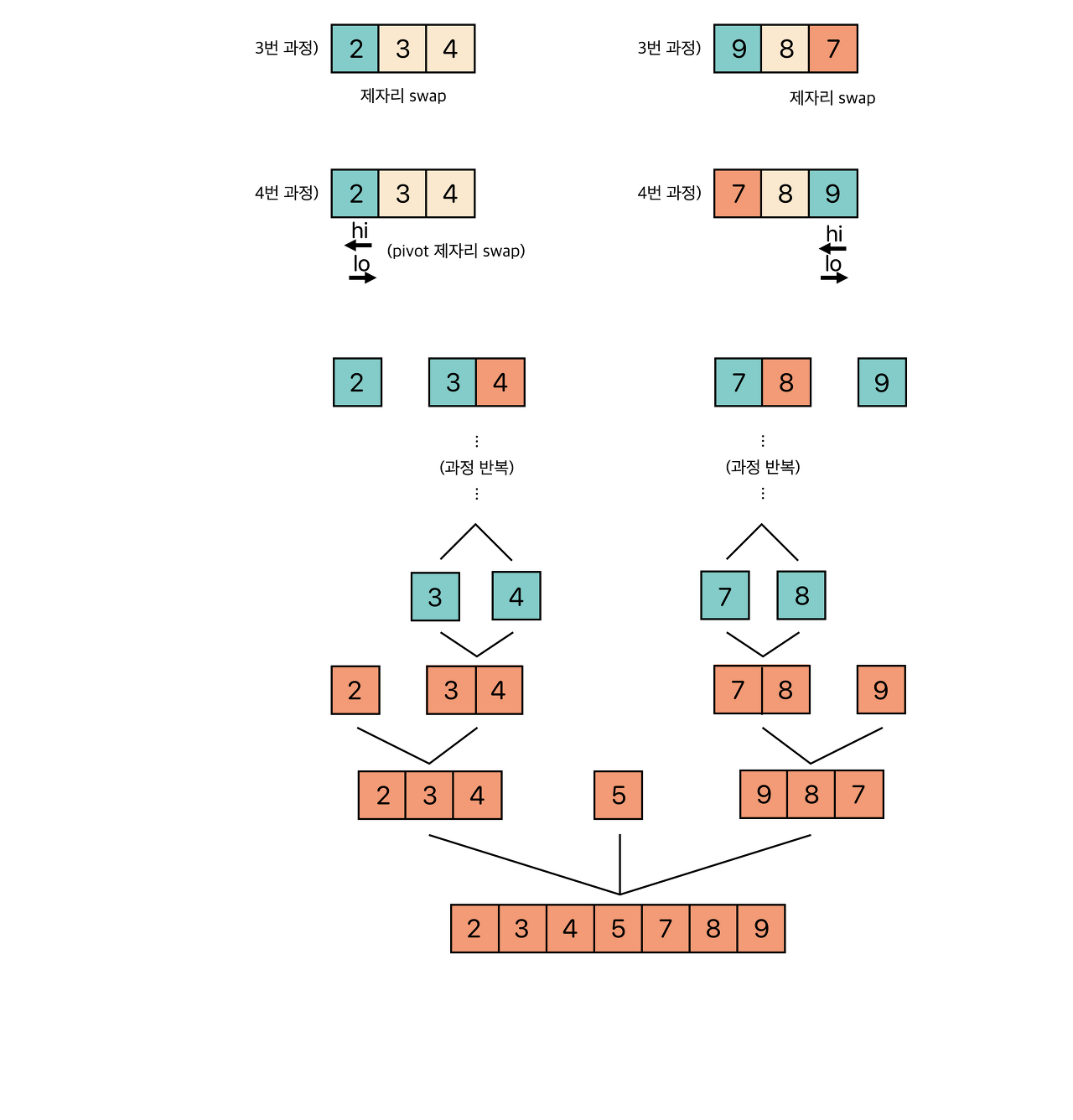
간단하게 주석도 달아 놓았으니 천천히 코드를 따라가면 이해하기 수월할 것이다.
오히려 주석때문에 코드 보기가 번거롭다면, 복사해서 주석을 없앤 뒤 로직을 따라가보면 된다.
생각보다 코드가 짧고 간단하게 구현되니 어렵진 않을거라 생각한다.
public class QuickSort {
/**
* @param a 정렬할 배열
* @param lo 현재 부분배열의 왼쪽
* @param hi 현재 부분배열의 오른쪽
*/
private static void l_pivot_sort(int[] a, int lo, int hi) {
// lo >= hi 이면 정렬할 원소가 1개 이하이므로 return
if (lo >= hi) {
return;
}
// 피벗을 기준으로 요소들이 왼쪽과 오른쪽으로 약하게 정렬 된 상태로 만들어 준 뒤,
// 최종적으로 pivot의 위치를 얻는다.
int pivot = partition(a, lo, hi);
// 이후 해당 피벗을 기준으로 좌, 우를 부분리스트로 나누어 분할-정복을 수행
l_pivot_sort(a, lo, pivot - 1);
l_pivot_sort(a, pivot + 1, hi);
}
private static int partition(int[] a, int left, int right) {
int lo = left;
int hi = right;
int pivot = a[left]; // 부분리스트의 왼쪽 요소를 피벗으로 설정
// lo가 hi보다 작을 때 까지만 반복한다.
while (lo < hi) {
/*
* hi가 lo보다 크면서, hi 위치의 값이 pivot보다 작거나 같은 원소를
* 찾을 때 까지 hi를 감소시킨다.
*/
while (a[hi] > pivot && lo < hi) {
hi--;
}
/*
* hi가 lo보다 크면서, lo 위치의 값이 pivot보다 큰 원소를
* 찾을 때 까지 lo를 증가시킨다.
*/
while (a[lo] <= pivot && lo < hi) {
lo++;
}
// 찾은 두 요소를 바꾼다.
swap(a, lo, hi);
}
/*
* 마지막으로 맨 처음 pivot으로 설정한 위치 a[left)의 값과
* lo가 가리키는 원소를 바꾼다.
*/
swap(a, left, lo);
// 위에서 값을 바꿨으므로 pivot은 lo에 위치하므로 lo를 반환
return lo;
}
private static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}우선, l_pivot_sort 메소드에 정렬할 배열, 해당 배열의 왼쪽 인덱스, 가장 오른쪽의 인덱스를 인수로 전달하면 된다.
이후, partition 에서, 받은 리스트의 왼쪽 요소를 pivot으로 설정하여
pivot 보다 작은 요소들은 왼쪽에, pivot보다 큰 요소들은 오른쪽에 약한 정렬을 수행한 뒤,
반환 된 pivot의 위치를 기준으로 왼쪽과 오른쪽 부분리스트로 나누어 재귀적으로 분할과 정복을 수행하는 것이다.
퀵 정렬에 대해 간단하게 살펴보았고, 이제 병합 정렬에 대해 알아보자.
🔎 병합 정렬(Merge Sort)
- 배열을 반으로 나누어 각각 정렬한 후, 병합하는 과정을 통해 전체 배열을 정렬하는 방법
동작방식
1. 주어진 리스트를 절반으로 분할하여 부분리스트로 나눈다. (Divide : 분할)
2. 해당 부분리스트의 길이가 1이 아니라면 1번 과정을 되풀이한다.
3. 인접한 부분리스트끼리 정렬하여 합친다. (Conquer : 정복)아래의 그림을 보면 과정 자체는 쉽게 이해할 수 있을 것이다.
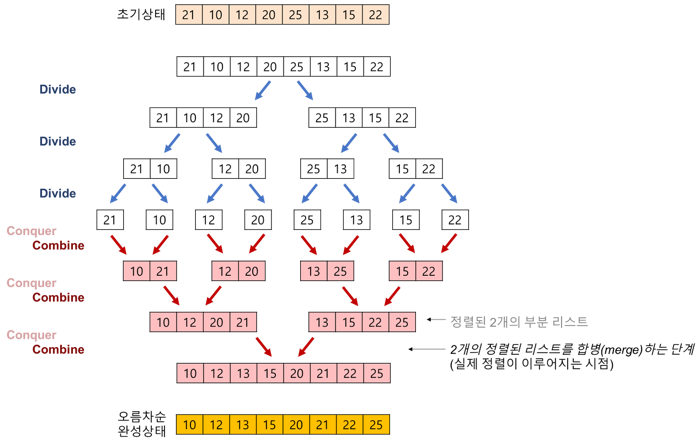
근데 이때 마지막 이전 부분에서 두 부분리스트를 어떻게 정렬하고 합칠까?
일단 각각의 부분리스트가 정렬된 상태 이므로 합쳐서 정렬할 때 굳이 삽입, 버블 정렬 등을 활용할 필요가 없고, 각 부분리스트의 첫 번째 원소부터 순차적으로 비교만 해주면 된다.
그렇다면 실제 구현은 어떻게 하는지 보자.
public class MergeSort {
private static int[] sorted; // 합치는 과정에서 정렬하여 원소를 담을 임시배열
public static void merge_sort(int[] a) {
sorted = new int[a.length];
merge_sort(a, 0, a.length - 1);
sorted = null;
}
private static void merge_sort(int[] a, int left, int right) {
if (left == right) return;
int mid = (left + right) / 2; // 절반 위치
merge_sort(a, left, mid); // 절반 중 왼쪽 부분리스트(left ~ mid)
merge_sort(a, mid + 1, right); // 절반 중 오른쪽 부분리스트(mid+1 ~ right)
merge(a, left, mid, right); // 병합작업
}
private static void merge(int[] a, int left, int mid, int right) {
int l = left; // 왼쪽 부분리스트 시작점
int r = mid + 1; // 오른쪽 부분리스트의 시작점
int idx = left; // 채워넣을 배열의 인덱스
while (l <= mid && r <= right) {
if (a[l] <= a[r]) {
sorted[idx++] = a[l++];
} else {
sorted[idx++] = a[r++];
}
}
if (l > mid) {
while (r <= right) {
sorted[idx++] = a[r++];
}
} else {
while (l <= mid) {
sorted[idx++] = a[l++];
}
}
// 정렬된 새 배열을 기존의 배열에 복사하여 옮겨준다.
for (int i = left; i <= right; i++) {
a[i] = sorted[i];
}
}
}우선, merge_sort 메소드에서 정렬할 배열을 받아 sorted를 해당 배열의 크기만큼 선언 후 중복정의된 세 개의 파라미터를 받는 merge_sort에 정렬할 배열, 가장 왼쪽 인덱스, 가장 오른쪽 인덱스를 전달한다.
이후 전달 받은 배열을 재귀를 통해 mid 값을 기준으로 왼쪽 부분리스트와 오른쪽 부분리스트로 나누고 left == right 즉, 리스트의 크기가 1이 되면, 반환되며 병합작업(merge)을 수행한다.
merge 메소드의 처음 나오는 while문은 두 부분리스트를 순차적으로 비교하며 한쪽의 리스트가 먼저 정렬될 때 까지 임시 공간인 sorted에 담는다.
이후 왼쪽이든 오른쪽이든 먼저 채워지는 곳이 생기면 while문을 나와 아직 남아있는 원소를 마저 채운다.
마지막으로 정렬된 새 배열을 기준의 배열에 복사하여 옮겨주는 것이다.
병합 과정이 이해가 안된다면 아래 이미지를 보도록 하자
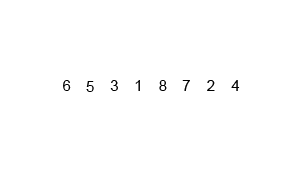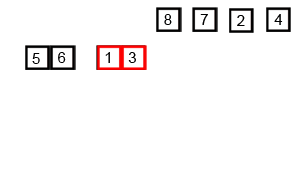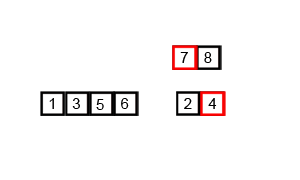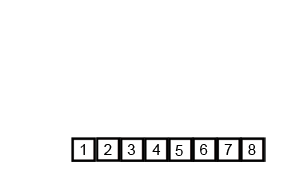 https://en.wikipedia.org/wiki/Merge_sort
https://en.wikipedia.org/wiki/Merge_sort여기까지 퀵 정렬과 병합정렬에 대해서 살펴보았다.
Reference
https://st-lab.tistory.com/250
https://adjh54.tistory.com/334#7

