[Python] Union-Find 알고리즘

정의

• 노드를 합치고, 부모 노드를 찾아 서로소 집합을 찾아내는 알고리즘
• 트리 구조를 활용

특징

• Union-find 알고리즘은 두 가지의 함수로 이루어진다
• Find : 두 노드의 부모 노드를 확인하여 같은 집합에 속하는 지를 확인
• Union : 두 부분집합이 같은 집합에 속하는 경우, 하나의 부분집합으로 합침. 일반적으로 값이 더 작은 족을 부모노드로 하여 합침
  두 원소의 부모 노드를 찾고, 번호가 큰 노드가 번호가 작은 노드의 부모를 가리키도록 함
• 특히 무방향 그래프 내에 사이클이 존재하는 지 확인할 때 유용하게 쓰임 (유향 그래프의 경우 dfs를 이용)
• Find 함수 부분을 경로 압축(Path Compression)을 통해 리팩토링 시 시간 복잡도가 감소

원리

https://www.geeksforgeeks.org

그래프의 간선정보를 순회하면서,

• 만약 a와 b 두 노드가 연결되어 있고, 같은 부모 노드를 가리킨 경우, 사이클이 존재한다고 판단
• 그렇지 않은 경우, 두 부분집합을 합치기 위한 union 함수를 실행.

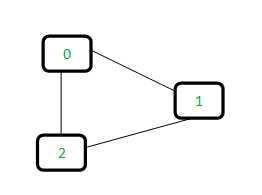
간선 0-1:

⇒ 0과 1을 정점으로 하는 부분집합을 찾는다

⇒ 0과 1은 각각 0과 1 부분집합에 속한다.

⇒ 두 부분집합은 다른 부분집합이므로, union을 수행하여 부분집합을 합친다.

⇒ 1번 노드를 0번 노드의 부모로 만든다. (0 ⊂ 1)
(union을 수행하기 위해서는, 노드 0을 노드 1의 부모노드로 만들거나 그 반대로 만들어야 한다.)

간선 1-2:

⇒ 1과 2는 각각 1과 2 부분집합에 속한다.

⇒ 두 부분집합은 서로 다르므로, union을 실행한다.

⇒ 2번 노드를 1번 노드의 부모 노드로 만든다. (0⊂1, 1⊂2)

간선 0-2:

⇒ 0과 2는 각각 0과 2 부분집합에 속한다.

⇒ 1은 0번 노드의 부모이고, 2는 1의 부모이므로, 0 또한 부분집합 2에 속한다.

⇒ 이렇게, 사이클이 형성된다.

구현

'''
TEST CASE
3
0 1
1 2
2 0
'''

def find(node):
    global parents
    if parents[node] == node:
        return node
    ret = find(parents[node]) # 재귀적으로 부모 노드 탐색
    parents[node] = ret # 부모 노드 갱신
    return ret # 부모 노드 반환

def union(a, b):
    global parents
    p_a, p_b = find(a), find(b)
    if p_a == p_b: return True # 부모가 같은 경우 True(사이클 존재)
    parents[p_b] = p_a

n = int(input()) # 간선 갯수
edge = [list(map(int, input().split())) for _ in range(n)] # 간선 정보
parents = list(range(3)) # 각 노드의 부모를 자기 자신으로 초기화

for i in range(n):
    a, b = edge[i]
    if union(a,b):
        print("사이클 발견")
        break
else:
    print("미발견")

문제

https://0x15.tistory.com/34

Introduction to Disjoint Set Data Structure or Union-Find Algorithm - GeeksforGeeks
https://boreum0302.github.io/algorithm/find-cycle/