[알고리즘/자료구조] 이진 탐색 트리(BST)

0. 🔖 목차

---

1. 이진 탐색 트리
   1-1 이진 탐색 트리 개념
   1-2 검색
   1-3 삽입
   1-4 삭제

1. 이진 탐색 트리

---

1-1. 이진 탐색 트리 개념

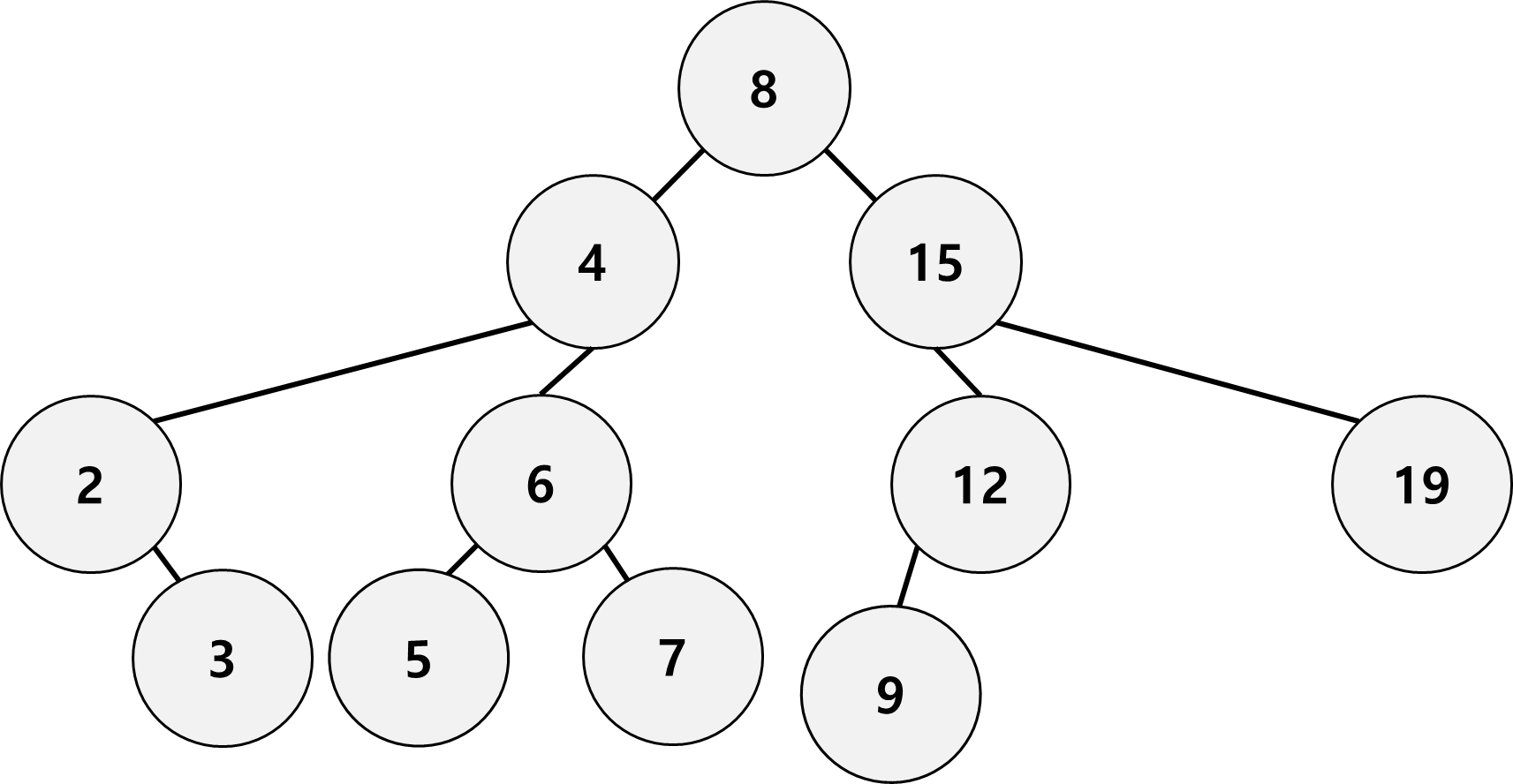
아래의 조건을 만족하는 트리를 이진 탐색 트리라고 한다.

• 각 노드에 값이 있다.
• 값들은 모두 비교 가능하다.
• 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
• 노드의 오른쪽 서브트리에는 그 노드의 값보다 큰 값들을 지닌 노드들로 이루어져 있다.
• 좌우 하위 트리는 각각이 다시 이진 탐색 트리여야 한다.

1-2. 검색

이진 탐색 트리는 이름 답게 탐색이 빠르다.

값들이 이진 탐색 트리에 저장되어있고 그중에 우리가 특정 값을 찾고자 할 때 최악의 경우$O(logn)$의 복잡도로 찾을 수 있다.

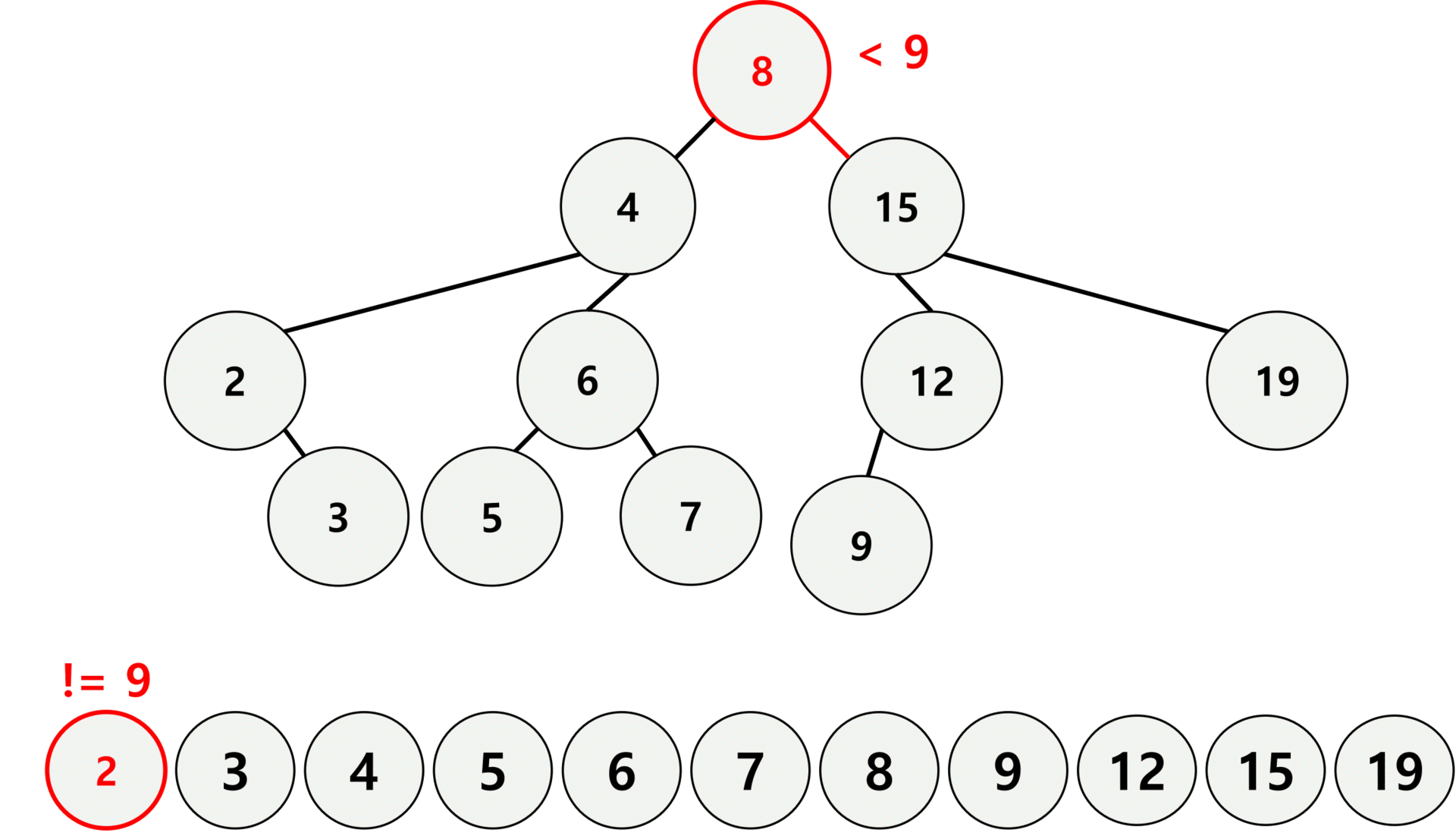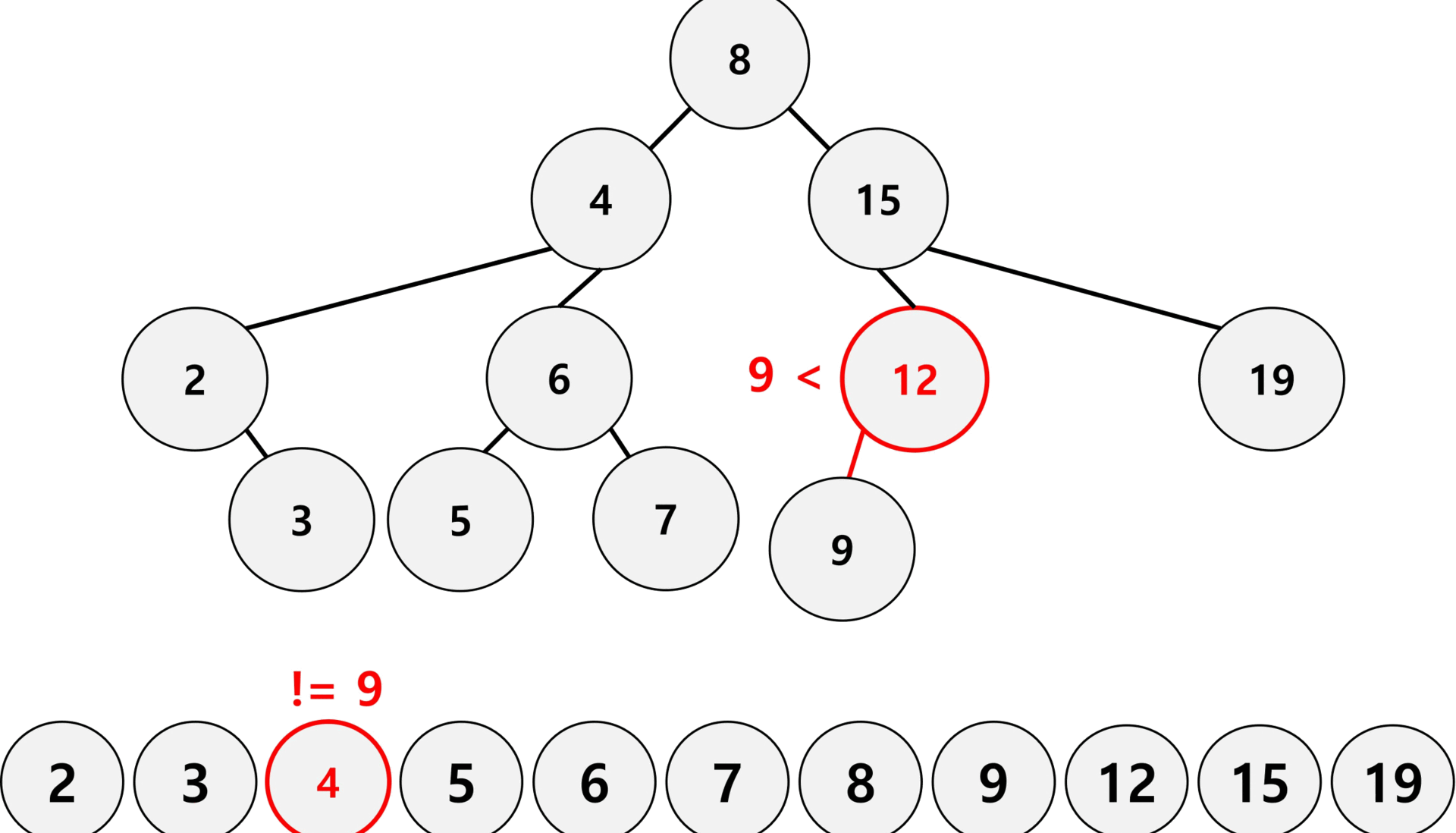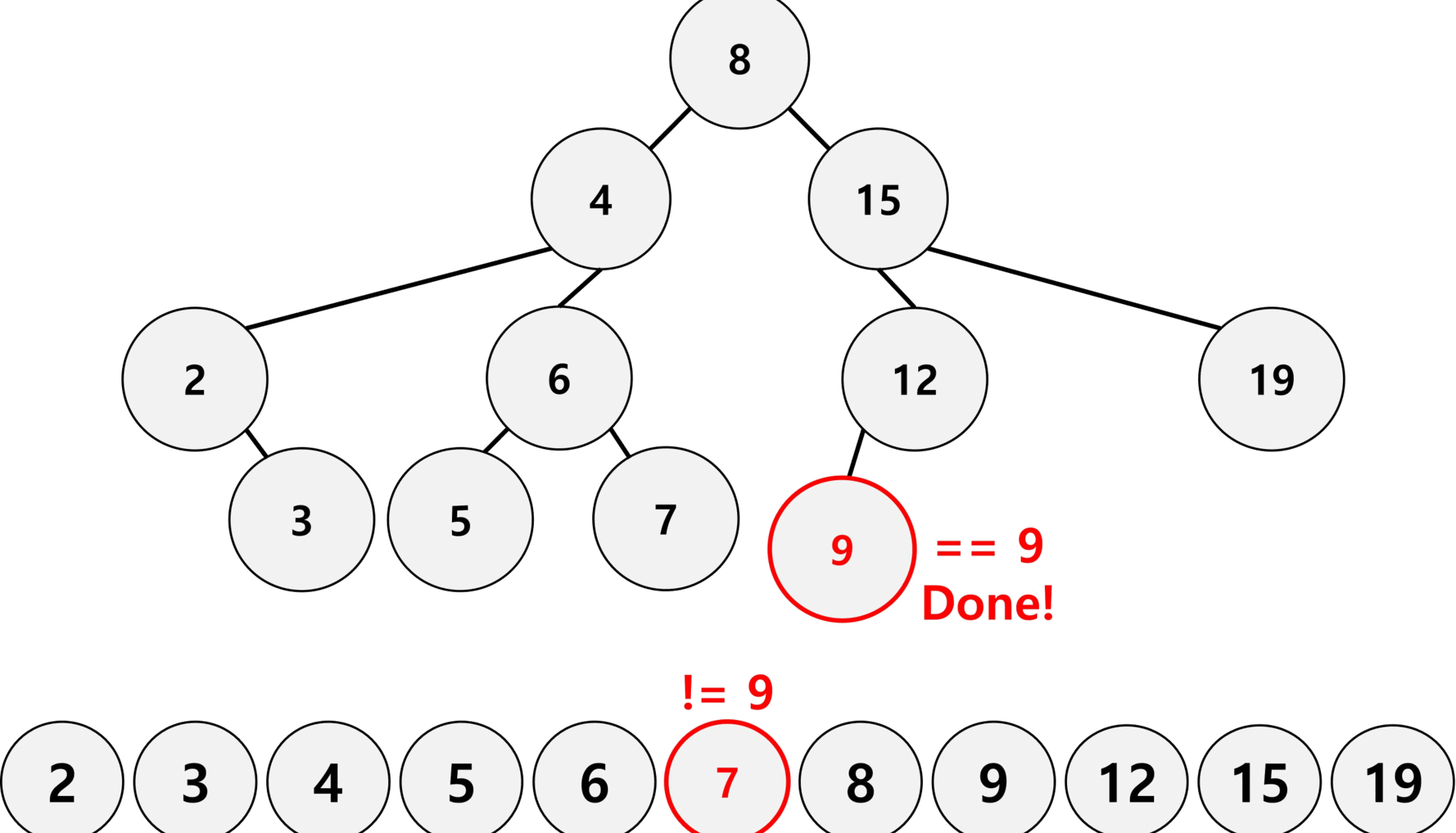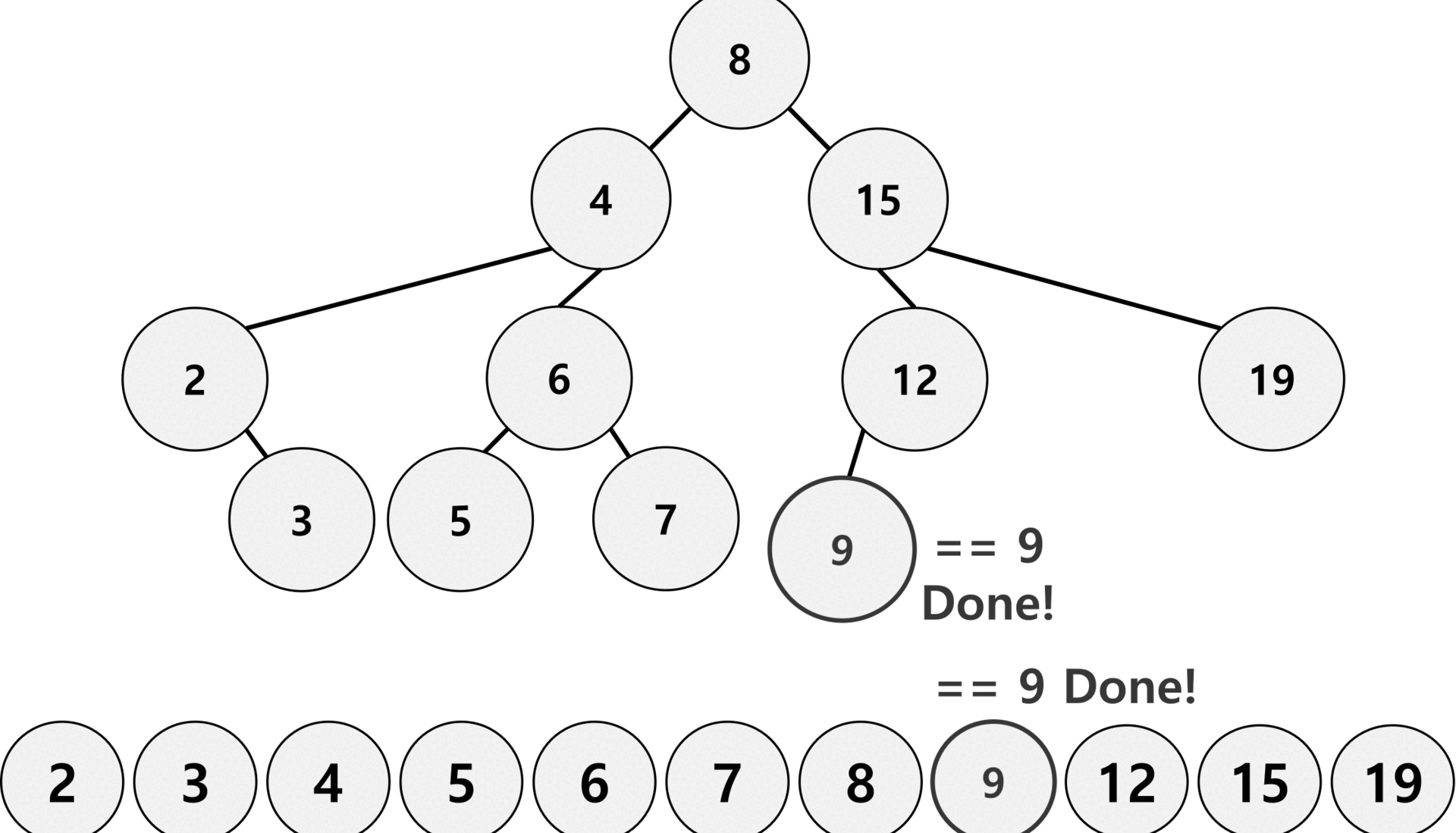
위 gif는 이진 탐색 트리와 일반 리스트에서 9를 찾는 과정이다.

이진 탐색 트리는 루트노드부터 찾고자 하는 수와 비교하여 작으면 왼쪽, 크면 오른쪽으로 이동하여 탐색 범위를 절반씩 줄여 일반 리스트보다 속도가 빠르다.

1-3. 삽입

그럼 이러한 이진 트리는 어떻게 만들까?

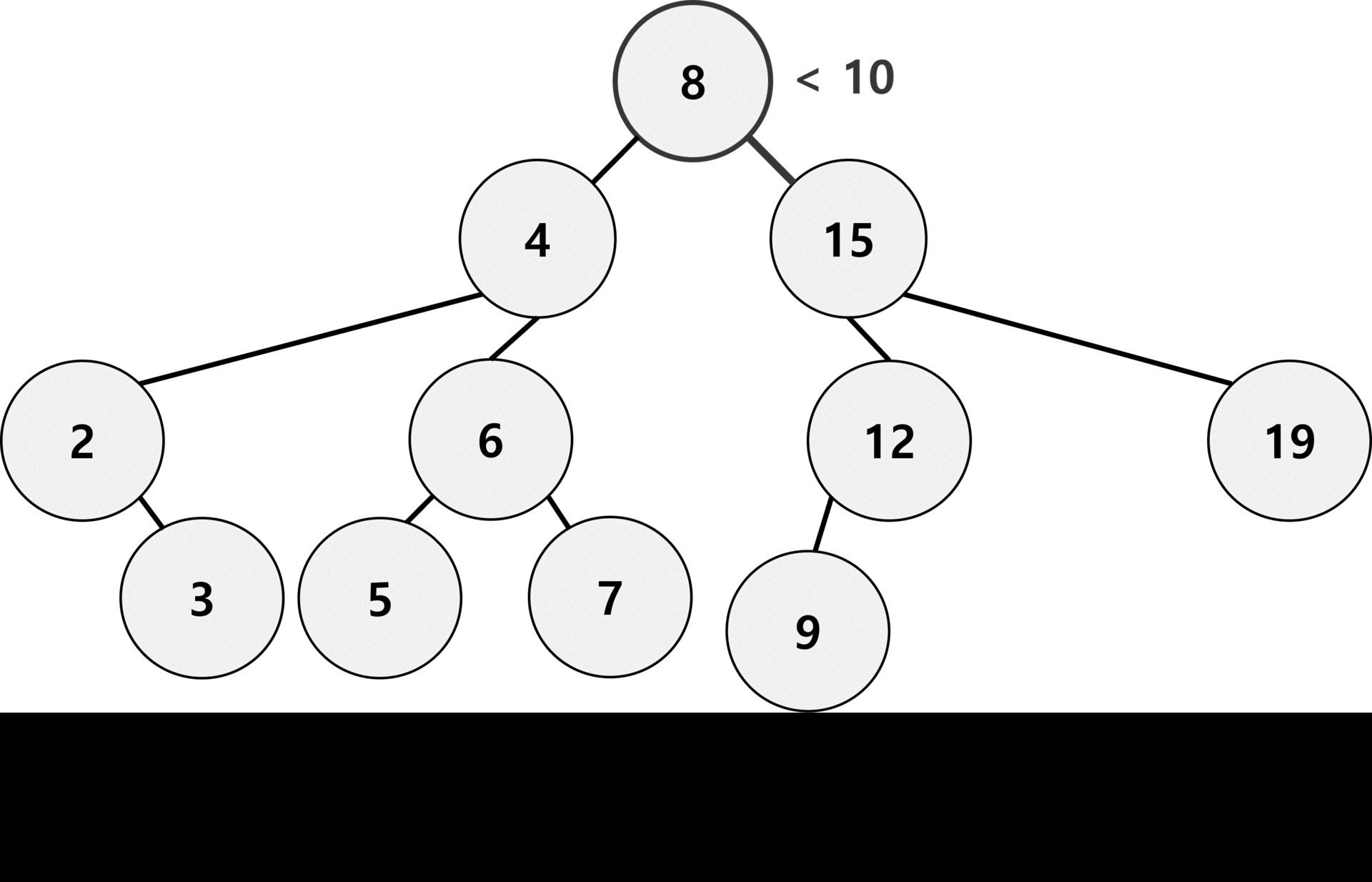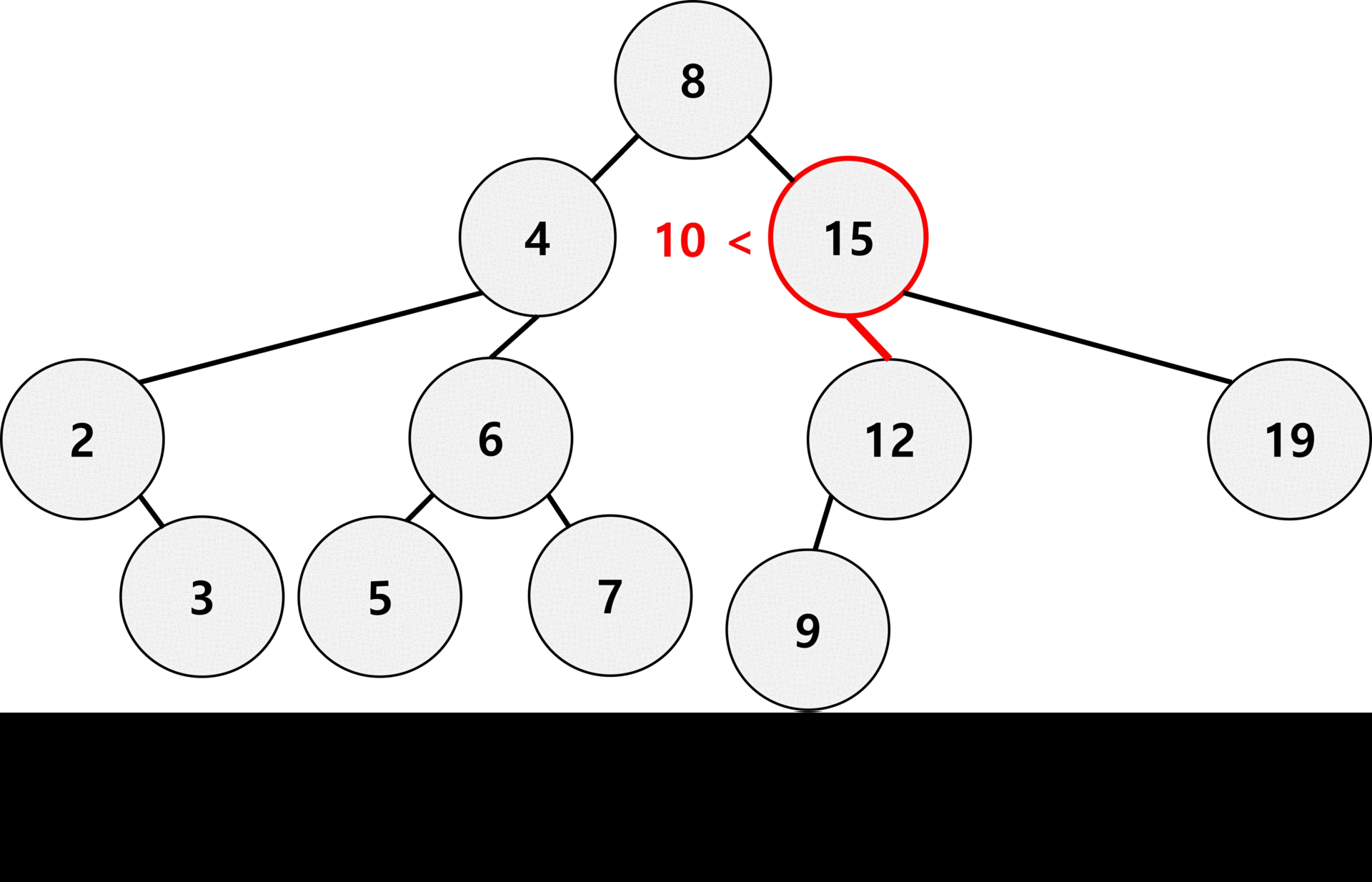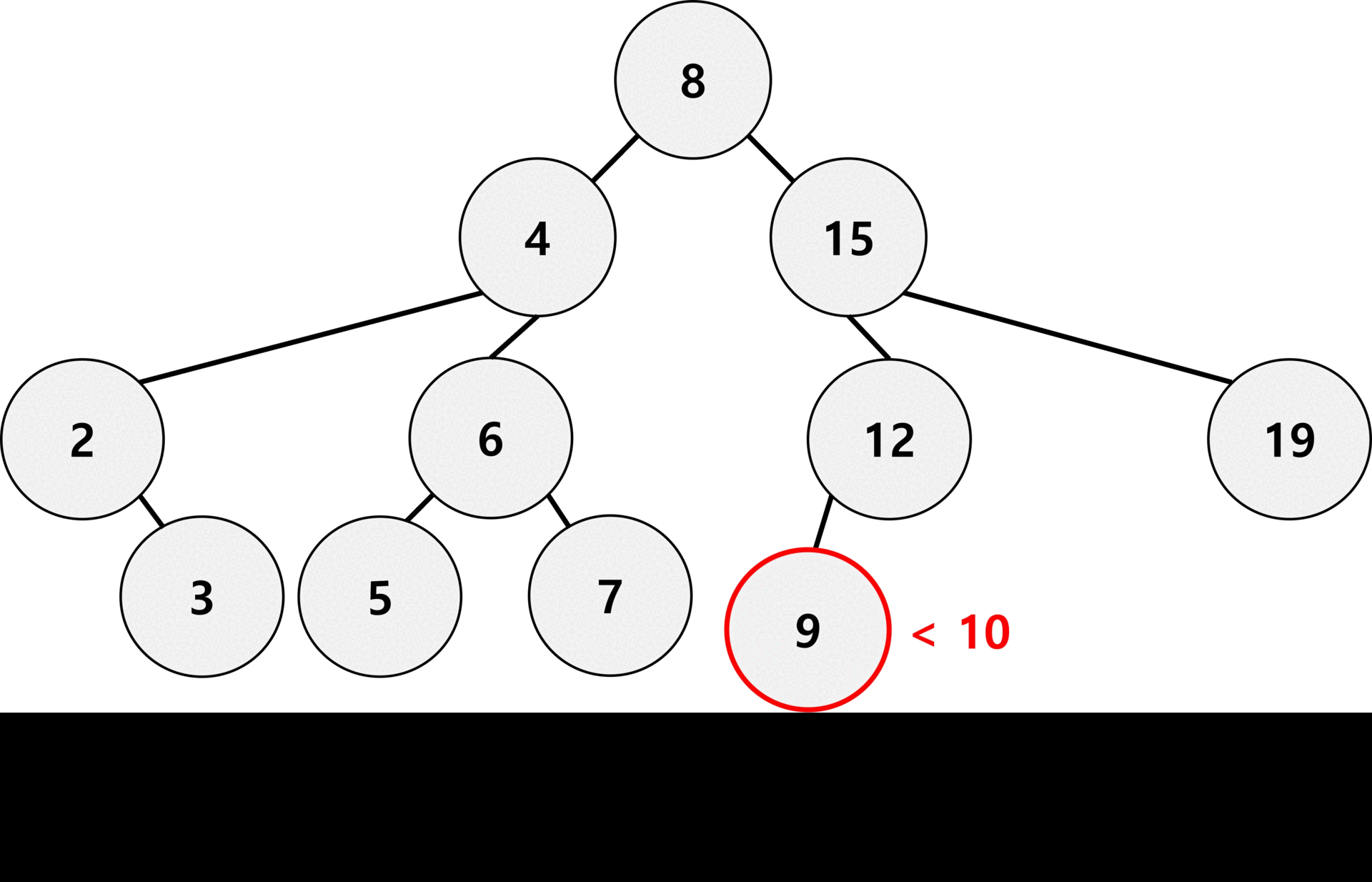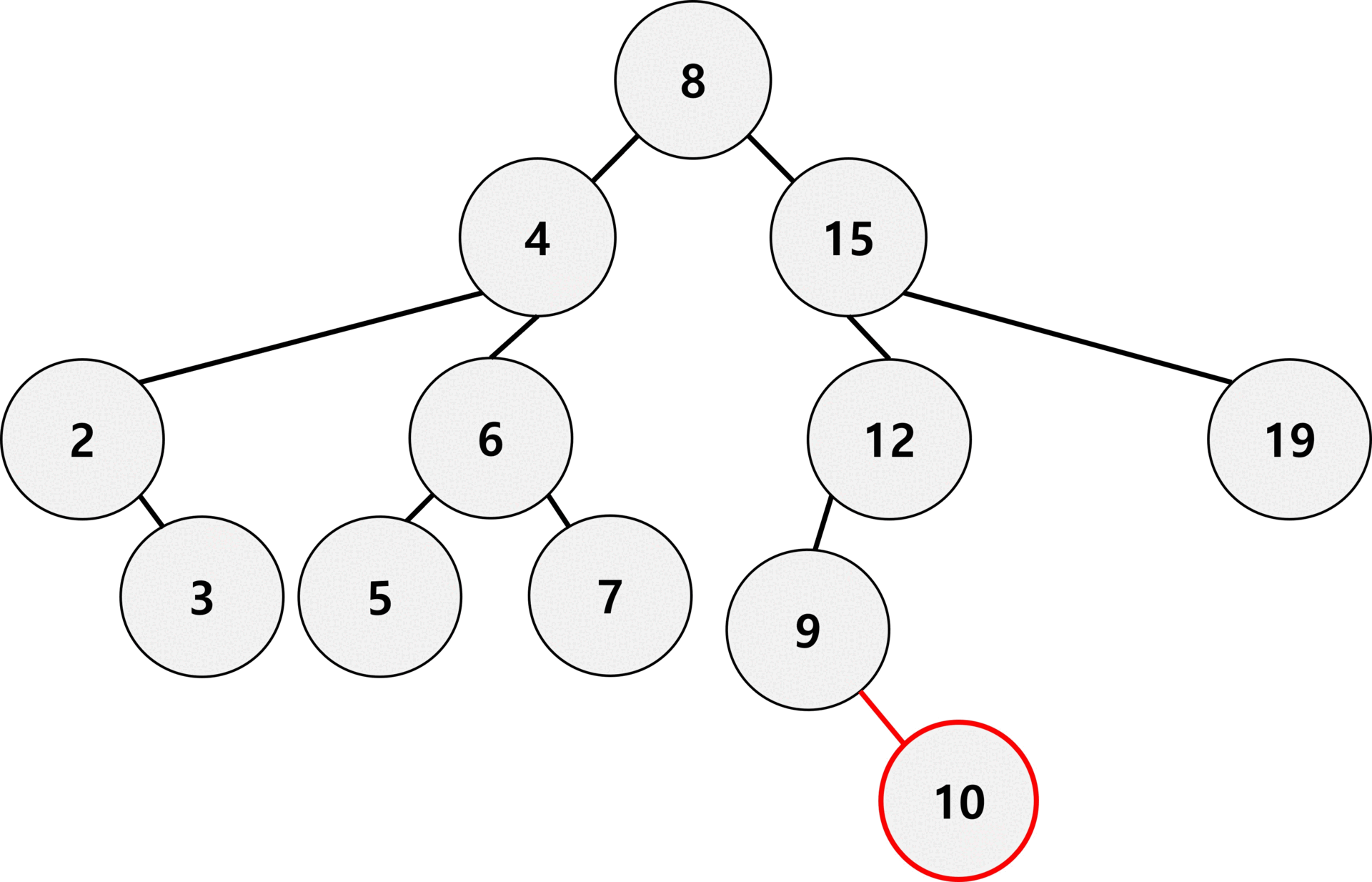
위 gif는 이진 탐색 트리에 10을 삽입하는 과정이다.

제일 먼저 10에 대한 검색을 진행한다. 그리고 마지막 노드를 기준으로 작으면 마지막 노드의 왼쪽에, 크면 오른쪽에 배치한다.

이러한 삽입 방식으로 이진 탐색 트리를 만들 수 있다.

1-4. 삭제

아래 세 가지 경우에 따라 나뉜다.

1. 자식노드가 없는 노드: 해당 노드를 삭제
2. 자식노드가 1개인 노드: 해당 노드를 삭제하고 그 위치에 해당 노드의 자식노드 대입
3. 자식노드가 2개인 노드: 삭제하고자 하는 노드의 값을 해당 노드의 왼쪽 서브트리에서 가장 큰값으로 변경하거나, 오른쪽 서브트리에서 가장 작은 값으로 변경한 뒤, 해당 노드를 삭제