0. 🔖 목차
- B-Tree 개요
- B-Tree의 조건
- 검색, 삽입, 삭제
- B+Tree
1. B-Tree 개요
탐색 트리에서 검색하고자 하는 값의 비교가 되는 값을 키라고 한다.
이진 탐색 트리의 경우 하나의 노드에서 최대 두 개의 자식 노드로 분화하기 때문에 이 두 자식 노드를 비교하는 키는 하나이다.
B-tree는 이러한 키를 2개 이상으로 설정한 자료구조이다.
이진 트리의 경우 현재 노드의 값과 탐색해야할 부분 비교하여 절반씩 줄여나가면서 탐색 속도를 증가시켰다.
만약 하나만 비교하는게 아니라 3개, 4개씩 비교하면서 1/4씩 1/5씩 줄여 나간다면 더 빠르게 찾을 수 있지 않을까?
탐색 범위가 줄어들지만 비교 횟수가 많아지기 때문에 더 성능이 안좋아질까?
CPU 입장에서 데이터를 비교하는 것 보다 비교한 이후 다음 비교 데이터를 가져오는 과정이 더 오래 걸리기 때문에 비교를 많이 하고 비교 횟수를 줄이는 즉, 노드의 깊이가 길어지지 않는 B-tree가 더 효율적이다.
2. B-Tree의 조건
위키피디아에 나와있는 B-tree의 조건이다.
- Every node has at most m children.
- Every node, except for the root and the leaves, has at least ⌈m/2⌉ children.
- The root node has at least two children unless it is a leaf.
- All leaves appear on the same level.
- A non-leaf node with k children contains k−1 keys.
대충 번역하자면
- 모든 노드는 최대 m개의 자식 노드를 갖는다.
- M은 B-tree의 하이퍼파라미터이다. M이 특정된 경우 M차 B-tree라고 부른다.
- 내부 노드는 최소 ⌈m/2⌉개의 자식 노드를 갖는다.
- ⌈ ⌉는 반내림을 의미한다.
- 루트 노드가 리프 노드가 아닌 경우 루트 노드는 최소 2개의 자식 노드를 갖는다.
- 모든 리프 노드는 같은 레벨에 있어야 한다.
- 이 조건 덕분에 탐색 깊이가 일정하다
- 리프 노드가 아닌 모든 노드는 k개의 자식 노드를 가지고 있을 경우 k-1개의 키를 가져야 한다.
3. 검색, 삽입, 삭제
모든 삽입과 삭제 과정에서 위의 B-Tree 조건이 위배되는 경우가 존재할 수 있고 이를 해결하기 위한 방법이 존재한다.
일단 검색을 먼저 보자
검색
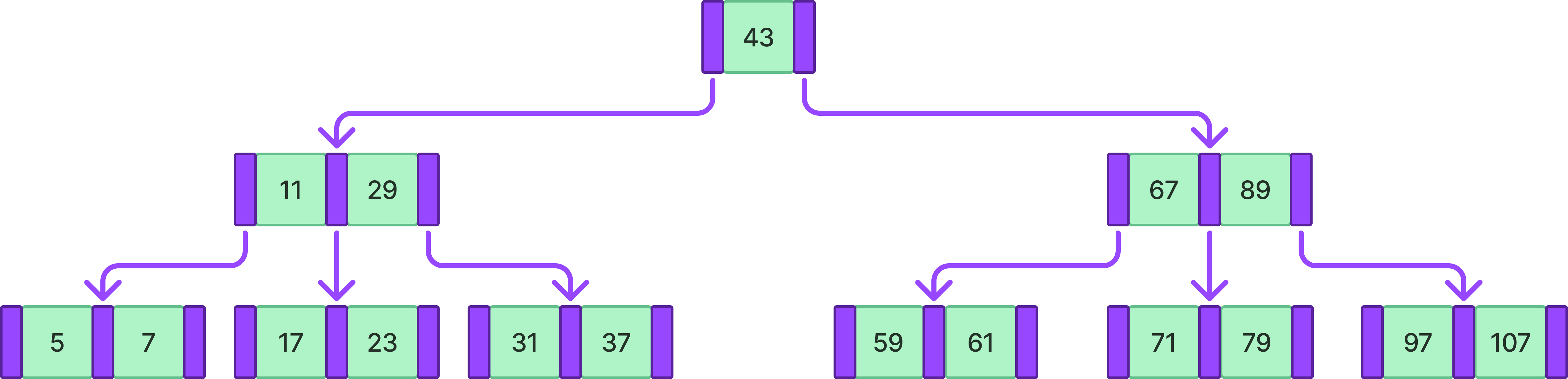
위와 같은 B-tree에서 71을 검색한다고 하자.
- 제일 먼저 루트노드인 43과의 비교를 한다. 43보다 크기 때문에 오른쪽 자식 노드로 이동한다.
- 오른쪽 자식 노드에서 71은 67보다 크고 89보다 작기 때문에 가운데 자식 노드로 이동한다.
- 가운데 자식 노드에서 71을 찾을 수 있다.
삽입
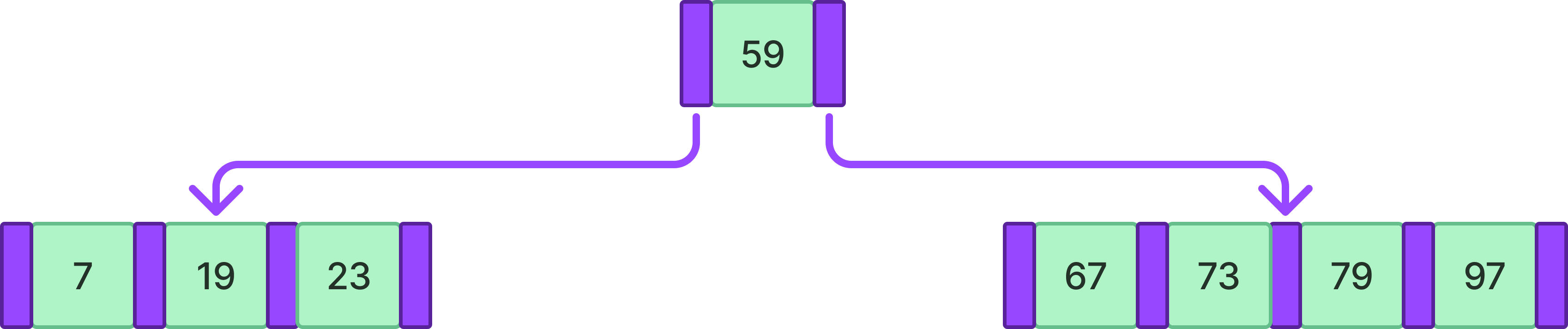
위와 같은 4차 B-tree에서 61을 삽입한다고 하자.
먼저 값을 삽입하기 좋은 위치를 찾기 위해 검색 과정을 수행하고 해당 값을 삽입한다.
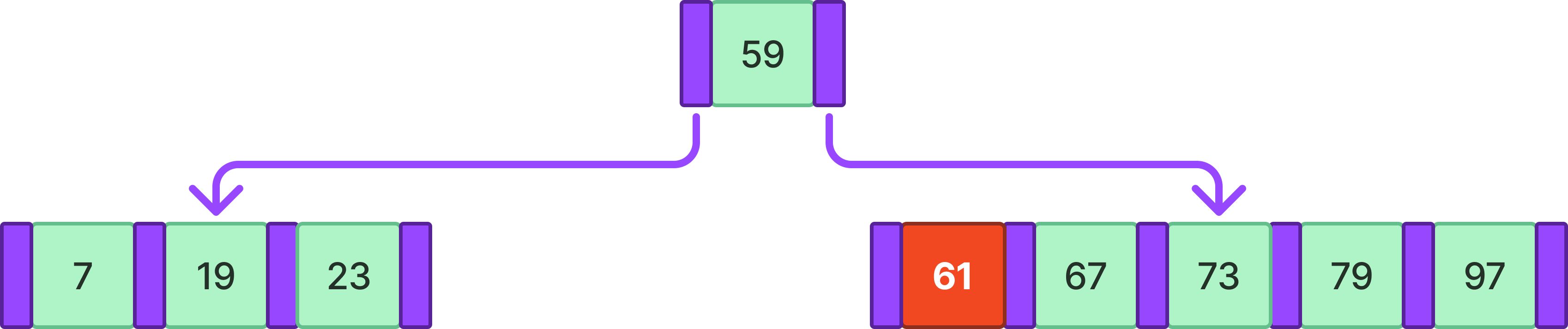
이때 B-tree의 조건을 위반하지 않는다면 그대로 넘어가면 되지만 예제에서는 조건 1번을 위배한다. 이러한 경우 위배하는 노드의 중앙 값을 부모 노드에 올리고 분리하여 해결한다.
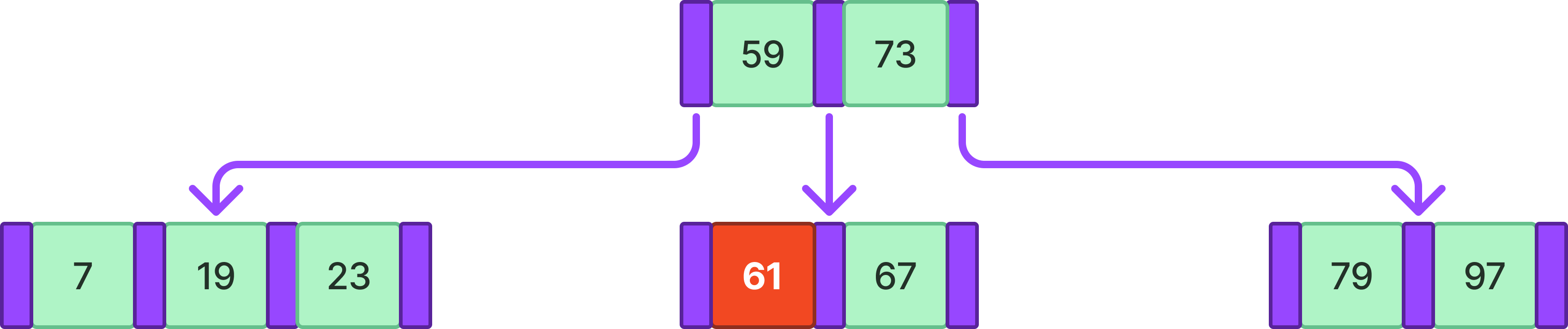
만약 중앙값을 부모노드에 올렸는데 이번엔 부모 노드가 1번 조건을 위배한다면?

위 경우에 23이라는 값을 삽입했을 때 조건 1이 위배되어 아까와 같은 과정을 거친다고 하자.


이번엔 부모 노드가 1번 조건을 위배한다. 이러면 부모 노드에 대해 아까 과정을 재귀적으로 반복하면 된다.
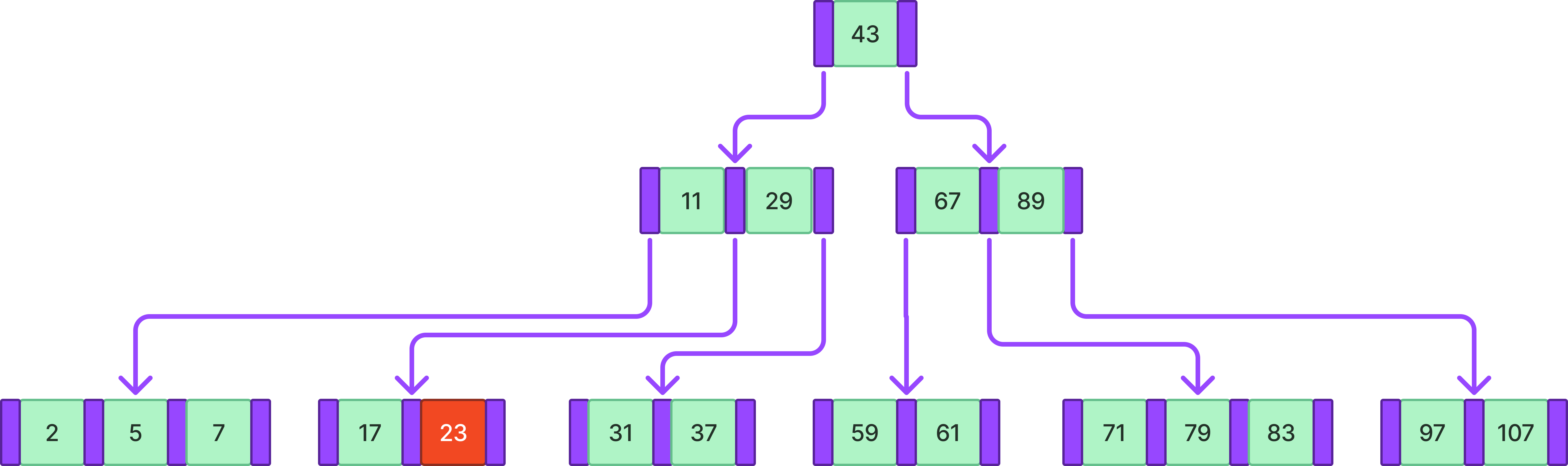
이러면 모든 삽입하는 경우에 대해서 조건을 위배하지 않도록 대처가 가능하다.
삭제
정의 부분에서 약간 헷갈리는 부분이 있어서 나중에 해결 후 정리
4. B+Tree
B-Tree와 달리 리프 노드에만 데이터를 저장하고 내부 노드에 키만 존재하는 트리 구조이다.
이때 리프노드는 Linked List 형태로 연결되어있다.
덕분에 B-Tree에 비해 범위 탐색이 쉽다.

