0. 🔖 목차
- 그리디 알고리즘
1-1. 개념
1-2. 적절한 문제
1. 그리디 알고리즘
1-1. 개념
탐욕 알고리즘은 모든 지역적 최적해를 선택하여 전역적 최적해에 근사하는 방법론이다.
쉽게 말해서 문제에서의 최적의 정답을 구하기 위해 결론에 도달하기 위한 매 부분 문제마다 가장 최적인 정답을 구해서 궁극적으로 가장 최적의 해를 구하는 방법이다.
물론 매 부분 문제마다 최적의 해를 구한다고 궁극적으로 최적의 해가 되리란 보장이 없다.

체스를 예로 들면, 백이 지금 바로 눈 앞의 먹음직스러운 폰을 폰으로 먹는다면 그 순간에서만큼은 최적의 해가 될 것이다.
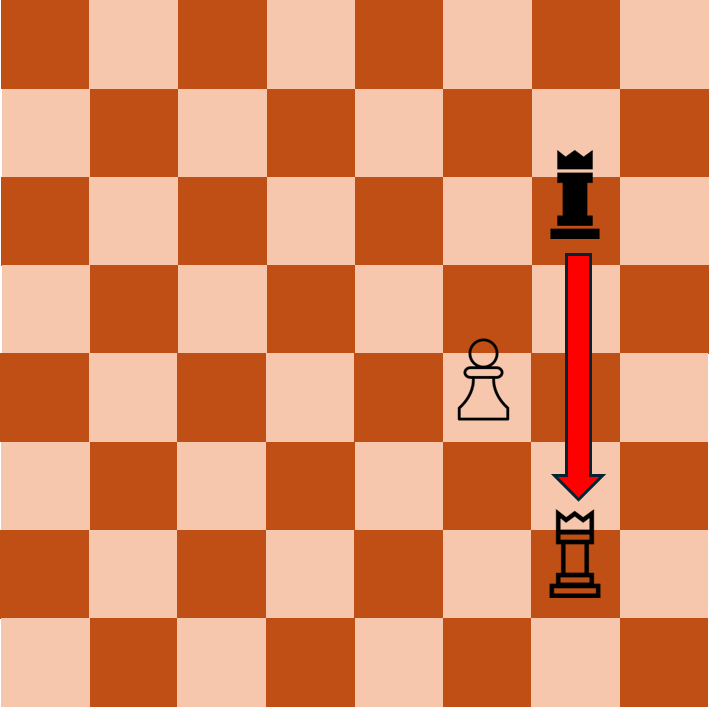
하지만 그 폰이 내 룩을 방어하고 있던 폰이기 때문에 결론적으로 내 룩이 먹히고 만다.
매 부분 문제마다 최적의 해를 좇았지만 궁극적인 최적해가 아닌 것이다. 이런 경우에는 그리디 알고리즘을 사용하면 안된다.
1-2. 적절한 문제
그렇다면 그리디 알고리즘을 사용하기 가장 적절한 문제들은 무엇이며 어떤 특징이 있는가?
- 탐욕스런 선택 조건(greedy choice property)
- 앞의 선택이 이후의 선택에 영향을 주지 않음
- 최적 부분 구조 조건(optimal substructure)
- 부분 문제에서의 최적해가 전체 문제에 대해서도 최적해

위의 최단 경로 찾기 문제를 보자. S에서 시작하여 E로 가기위해 경로 A, B중에 하나를 선택해야 한다.
이 문제에서 내가 경로 A를 선택하든 경로 B를 선택하든 이후의 경로 C를 지나는 것은 동일하므로 영향을 주지 않는다. 즉, 탐욕스런 선택 조건을 만족한다.
또한 이 문제에서 A를 골랐을 때 이동거리는 A의 길이 + C의 길이 이고
B를 골랐을 때 이동거리는 B의 길이 + C의 길이 이므로
A, B선택에서 경로가 더 짧은 A를 선택하는 것이 전체적인 문제(최단 경로 찾기)에서도 최적해가 된다.
따라서 이 문제는 탐욕스런 선택 조건, 최적 부분 구조 조건을 만족하기 때문에 그리디 알고리즘을 사용하는 것이 적절하다.
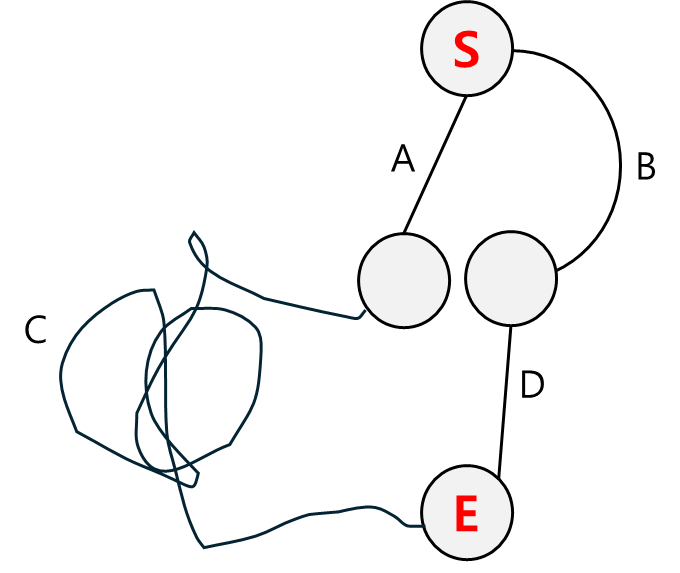
이 문제는 어떨까? A 경로를 고르면 무조건 C 경로를 가야하고, B 경로를 고르면 무조건 D 경로를 가야한다. 따라서 앞의 선택이 뒤의 선택의 영향을 준다. 즉, 탐욕스런 선택 조건을 만족하지 않는다.
만약 이 문제를 그리디 알고리즘으로 해결하려 한다면 처음 선택에서 무조건 A 경로를 고르게 될 것이다.

