[MP] Parallel Sorting

Sorting Algorithms

• Comparison based

  • quick sort, merge sort, etc.
  • $O(n \log n)$

• Non-comparison based

  • counting sort, radix sort, etc.
  • $O(n)$

• Parallel Comparison based ?

  • Ideal : $\frac{O(n \log n)}{n} = O(\log n)$

  • Similar with merge sort
    

  • Another example: Odd-Even Transposition Sort
    

  • $O(n)$

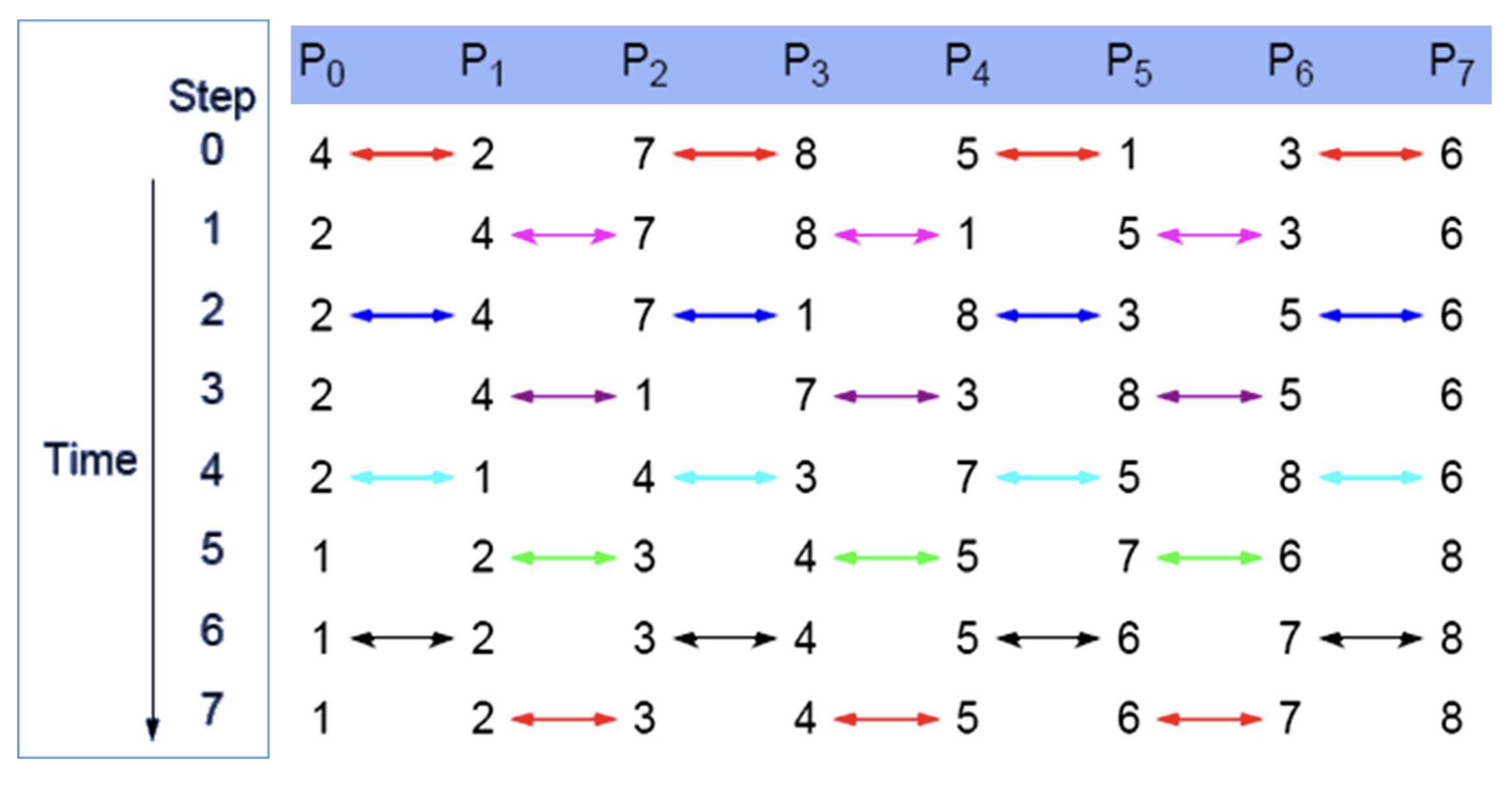
• Generally $n >> p$
  

• Time complexity:

  $T_{par} = (n/p)\log(n/p) + p\times(n/p) + p\times(n/p) = (n/p)\log(n/p) +2p(n/p)$

  (while ideal complexity's $O(\frac{\log n}{p})$)
  

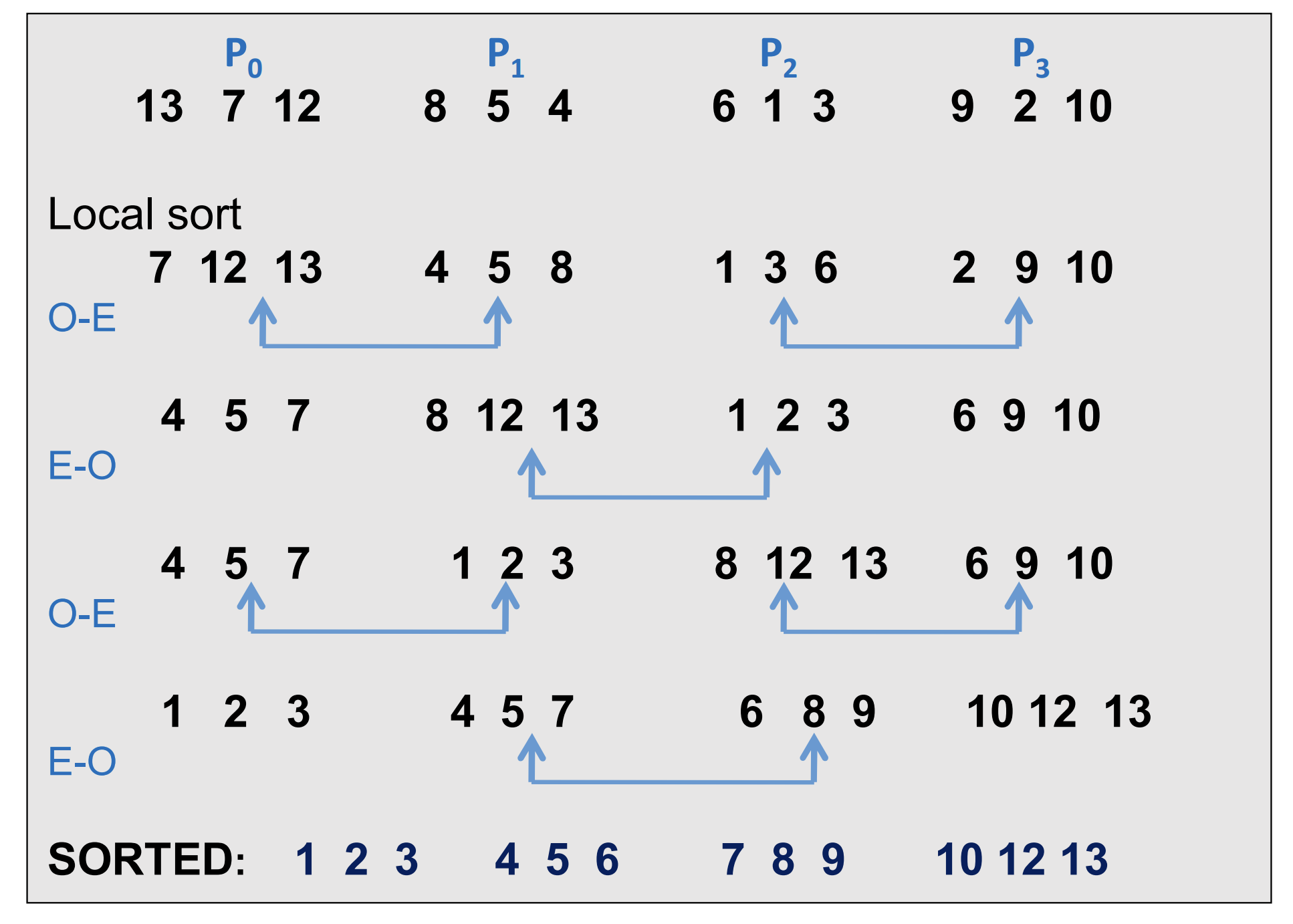
• Parallelizing Merge-Sort
  

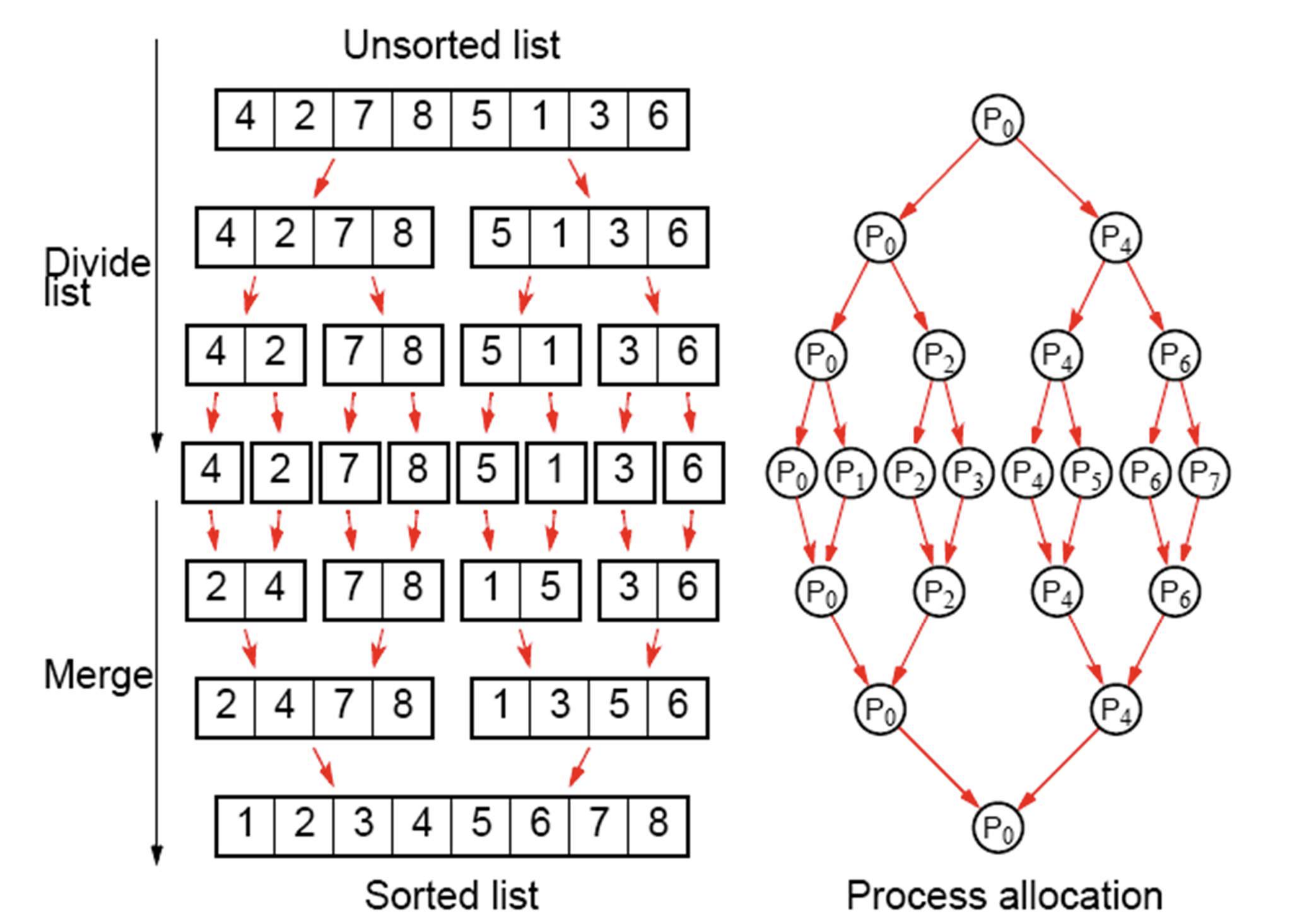
  • Sequencial: $T_{eq} = O(n\log n)$
  • Parallel: $T_{par} = 2\left(\frac{n}{2^1} + \frac{n}{2^2} + \cdots + 2 + 1\right) = O(4n)$

Bitonic Sequence

• $s = <a_0, a_1, \cdots, a_{n-1}>$ is bitonic means,
  $\exist_{i, 0\le i \le n-1}\;\;\;s.t\;\;s_{0..i}$ increases & $s_{i..n-1}$ decreases
• Let $s1= <\min(a_0, a_{n/2}), \min(a_1, a_{n/2 +1}) \cdots \min(a_{n/2-1},a_{n-1})>$
• Let $s2=<\max(a_0, a_{n/2}), \max(a_1,a_{n/2+1}) \cdots \max(a_{n/2-1},a_{n-1}) >$
• Then, it looks like..
  
• In semiconductor, there are two operators
• $\oplus$ : $x' = \min(x,y) \;\;\;\;\; y' = \max(x,y)$
• $\ominus$ : $x' = \max(x,y) \;\;\;\;\; y' = \min(x,y)$
  
  

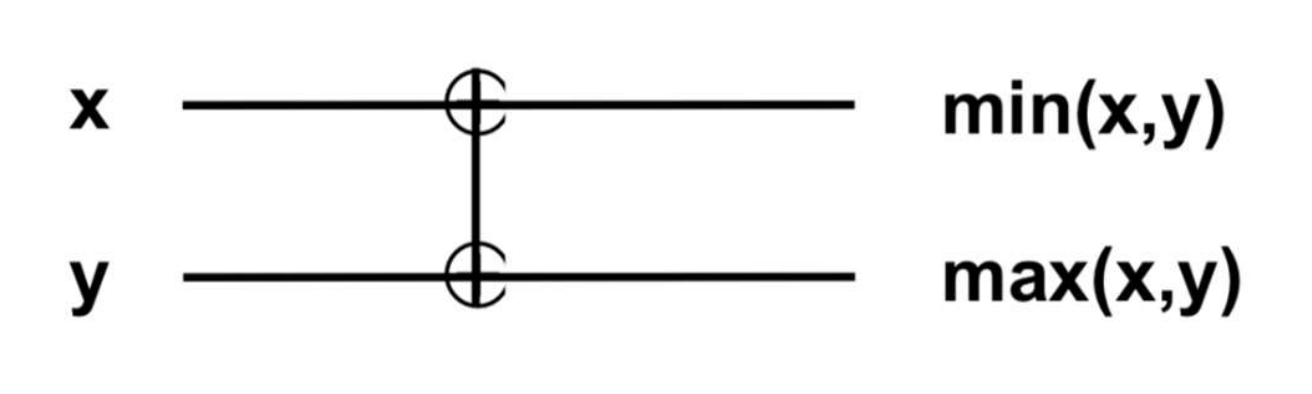
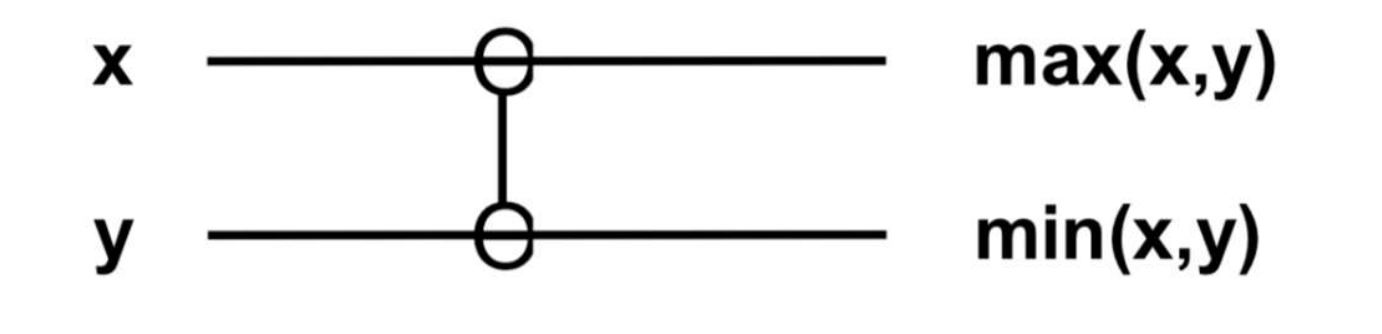
• Then sorting network looks like this.
  

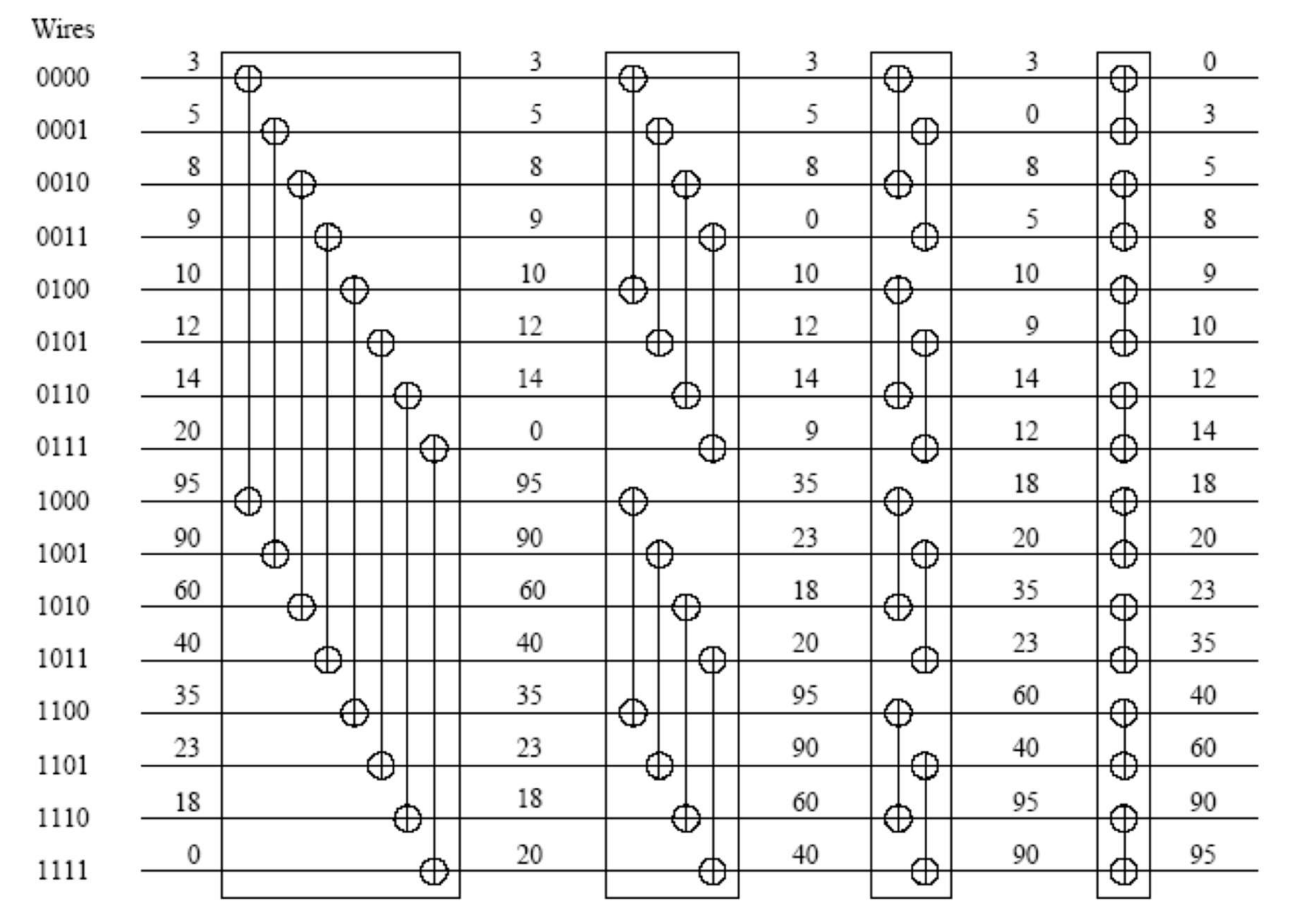
• How about non-sorted arrays? (not bitonic!)

• Network below builds bitonic sequence from unsorted arrays
  

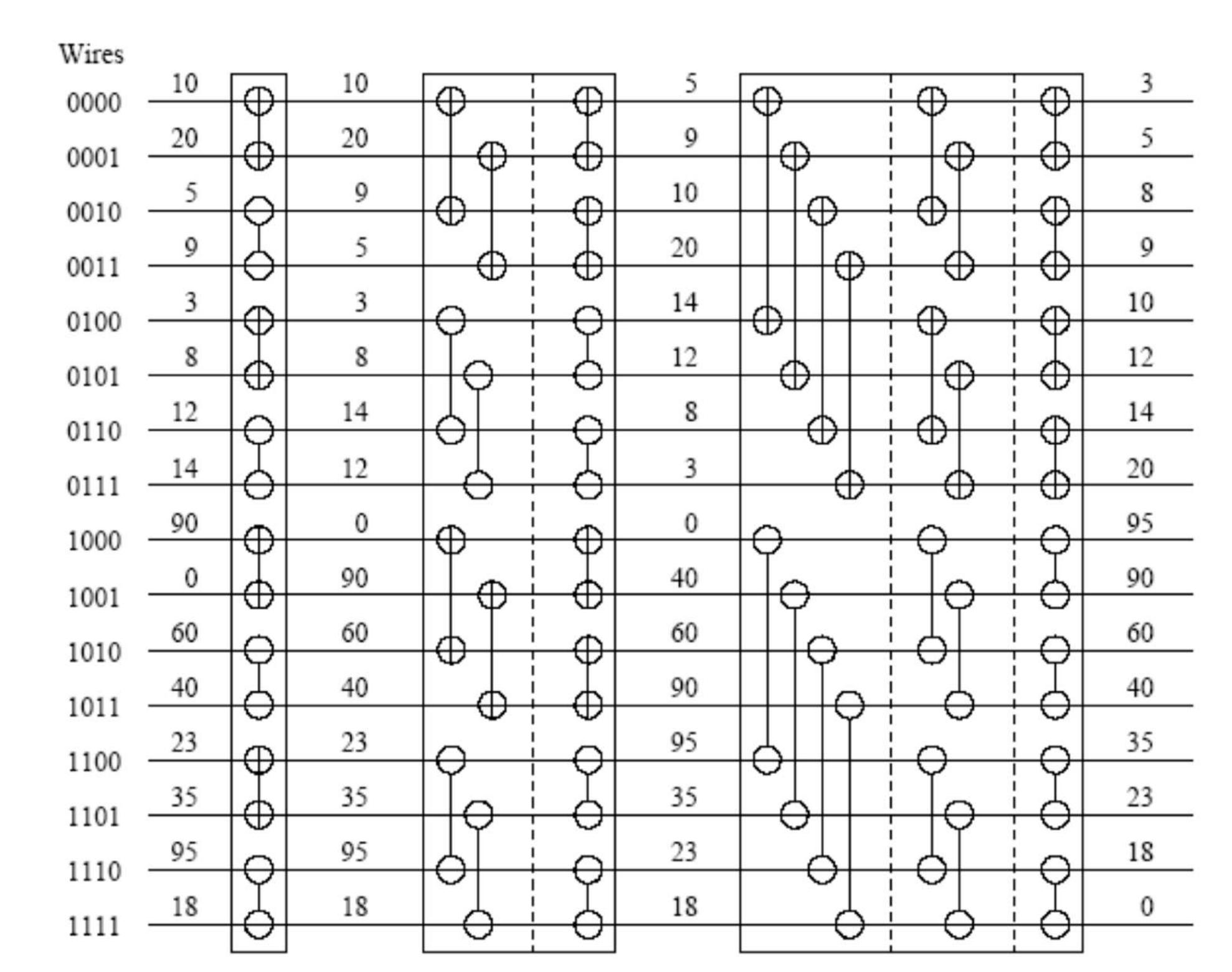
Shear sort

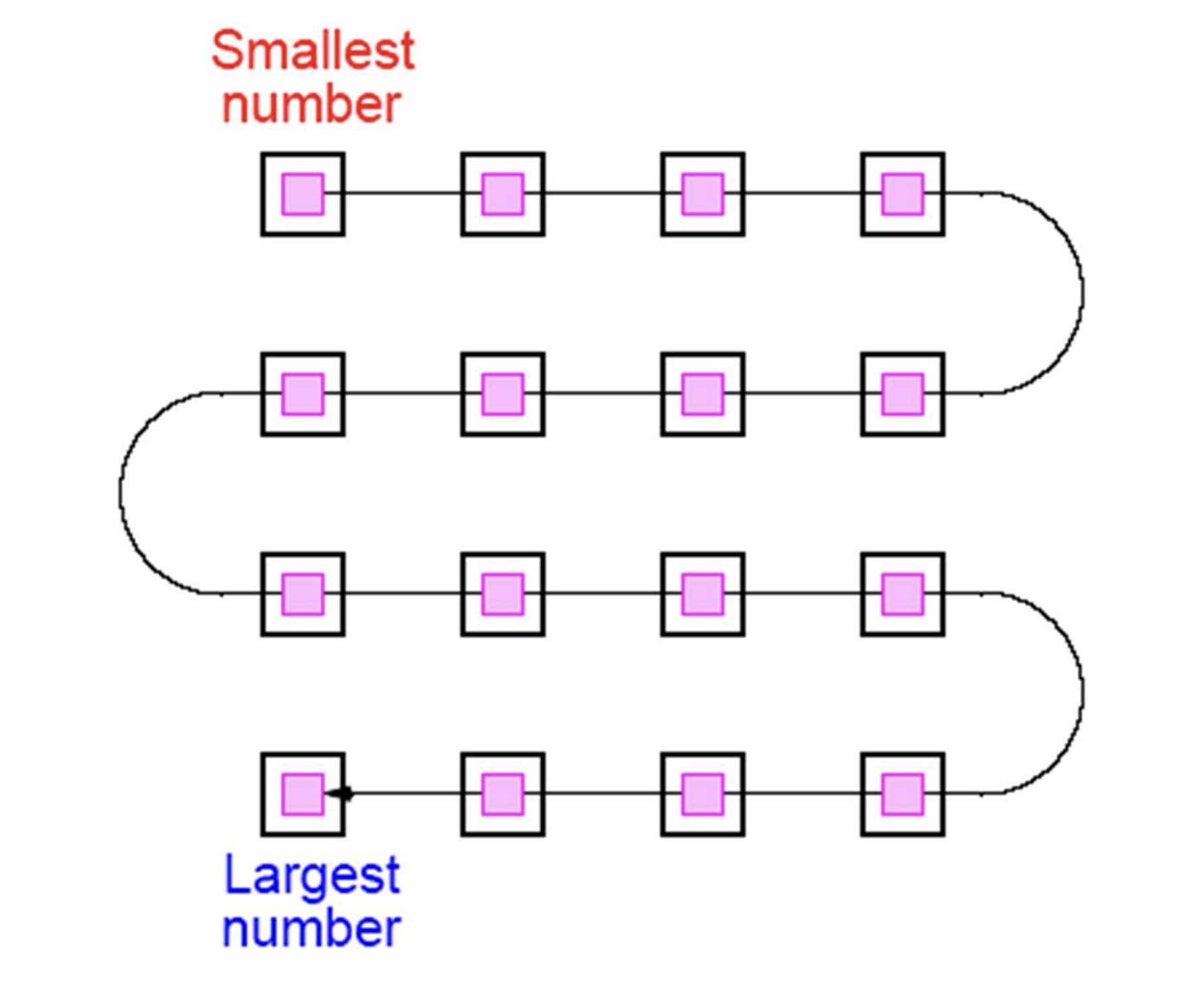
• Shear sort is a sorting algorithm to build a snake-like sequence using $n\times n$ mesh
  

• Alternate row and column sorting until list is fully sorted
  

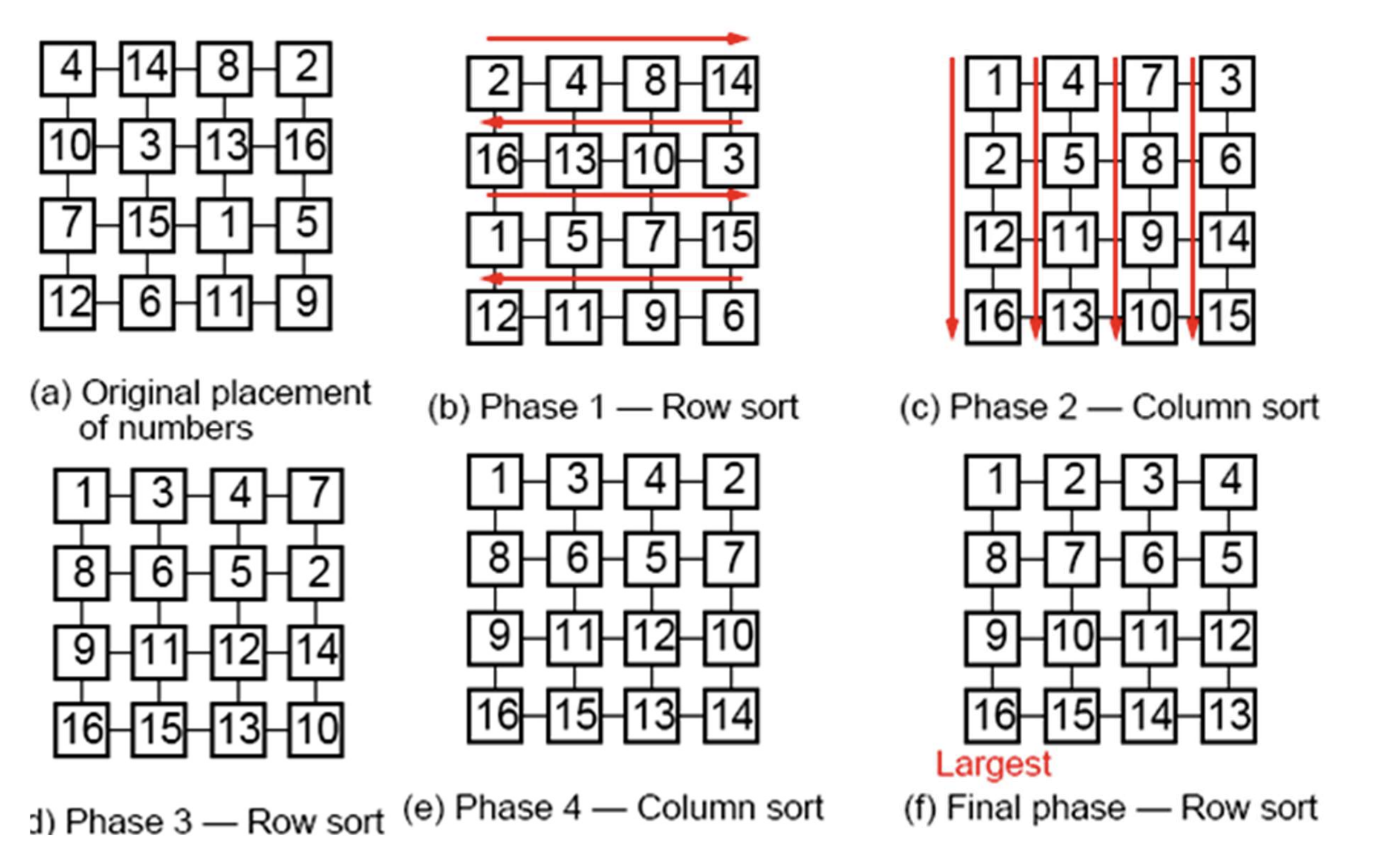
• Time complexity? (for $n \times n$ mesh)

  • Each step requires $O(n)$
  • One $n\times n$ mesh requires $\log(n^2)$ phases

Parallel Radix sort

• Similar with trump cards sorting
• counting sort for each digits, starts with least significant
• Key point : Should use stable sort

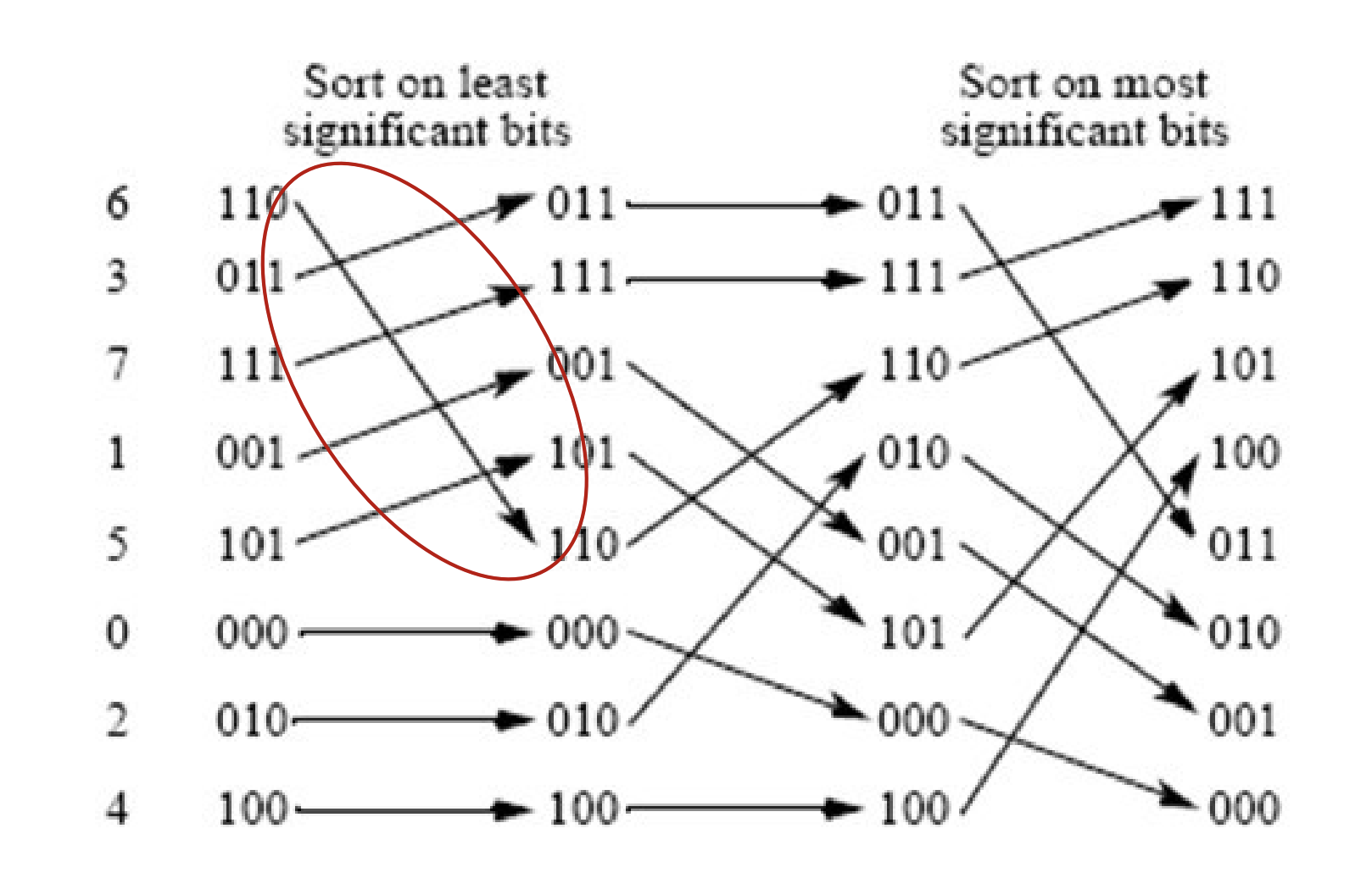
• Algorithm Overview

  1. Sequence: $7,14,4,1,6$

  2. Binary rep.: $0111_{2}, 1110_2, 0100_2, 0001_2, 0110_2$

  3. bit 0: $1, 0, 0, 1, 0$

  4. build histogram

     Zero	One
     3	2

  5. Calculate prefix sum for histogram

     Zero	One
     0	3

  6. Find offset: $0,0,1,1,2$

  7. Find index (offset + prefix sum) $3,0,1,4,2$

  8. Move values: $14,4,6,7,1$

  9. Repeat for all bits
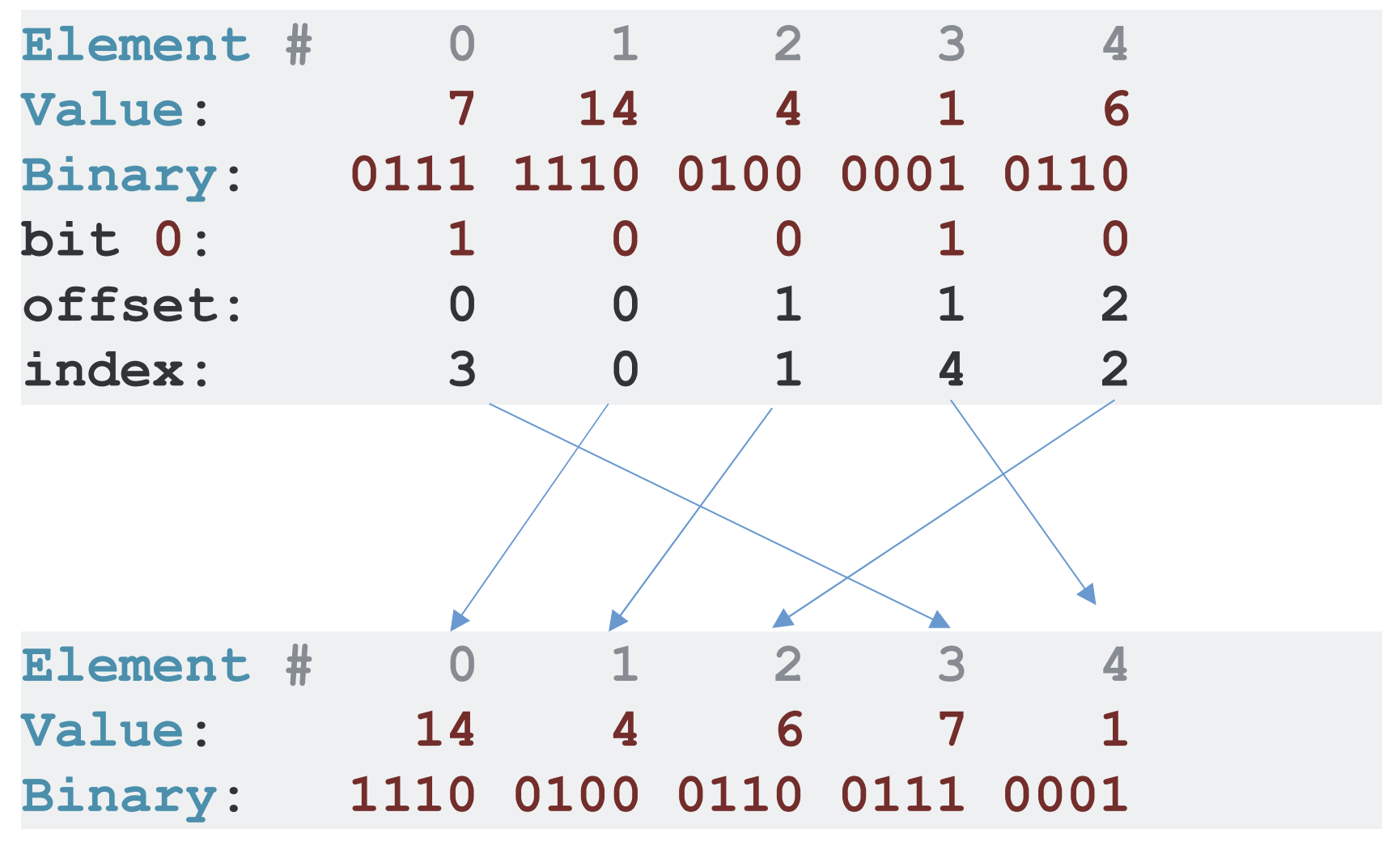