기수 정렬, 계수 정렬, 셸 정렬

기수 정렬(Radix Sort) : O(d(최대 자릿수)n)

• 낮은 자리수 부터 정렬하는 방식
• 각 원소 간의 비교 연산을 하지 않아 빠른 대신, 기수 테이블을 위한 메모리 필요

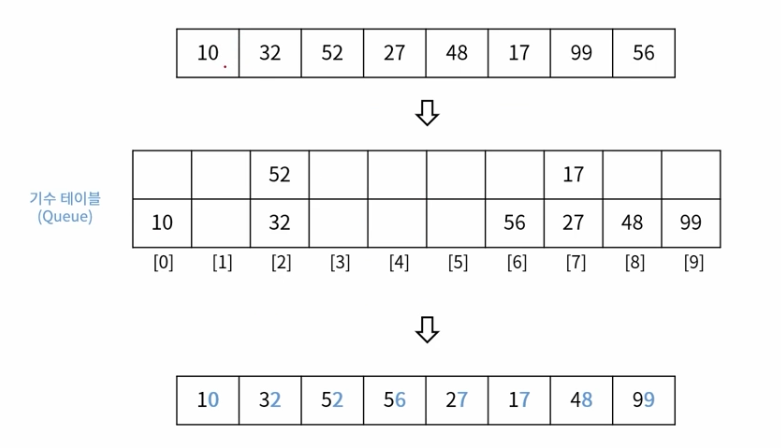
일의 자리를 기준으로 시작

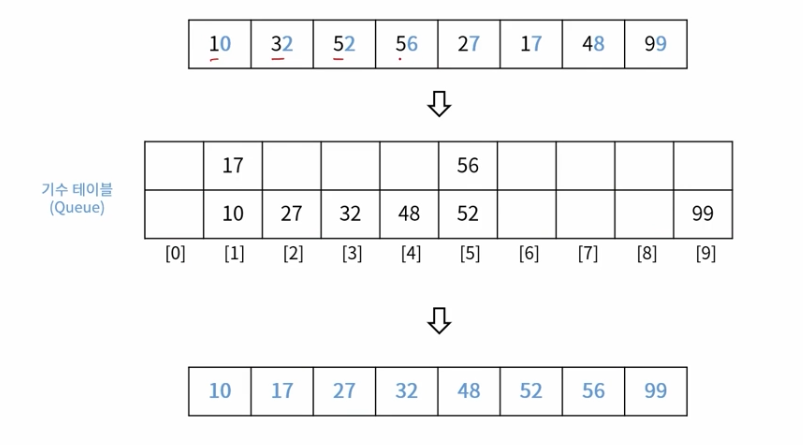
십의 자릿수를 기준으로

계수 정렬(Counting Sort) : O(n+k)

• 숫자 끼리 비교하지 않고 카운트를 세서 정렬하는 방식
• 카운트를 위한 메모리 필요
• k는 정렬 대상 중 최대값

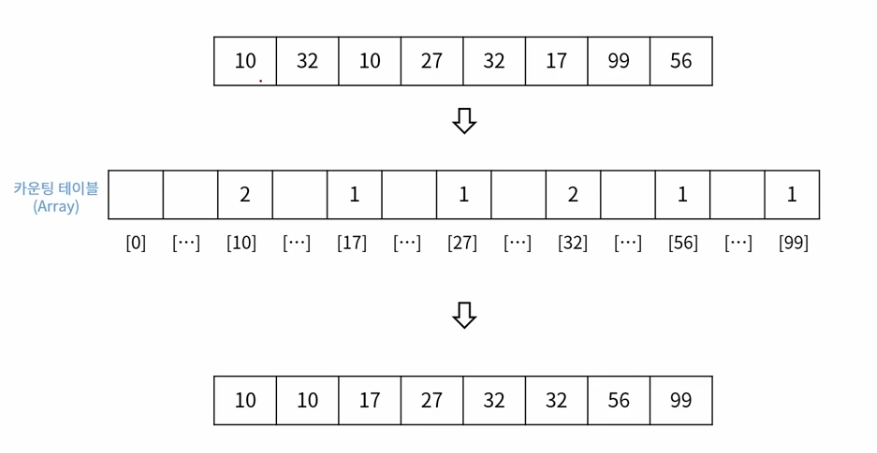
max값만큼 배열 사이즈를 잡아둠

다시 출력을 할때 0인지, 0이 아닌지 체크하고, 카운트만큼 출력

쉘 정렬(Shell Sort) : O(n^2)

• 삽입 정렬의 약점 보완
  -> 오름차순 정렬 기준, 내림 차순으로 구성된 데이터에 대해서는 앞의 데이터와 하나씩 비교하며 모두 교환 필요
• 이전의 모든 데이터와 비교하지 않고 일정 간격을 두어 비교

간격을 어떻게 설정하나에 따라 Worst case(ex: 다 내림차순)는 O(n^2)이지만 보통은 삽입 정렬보다 빠름

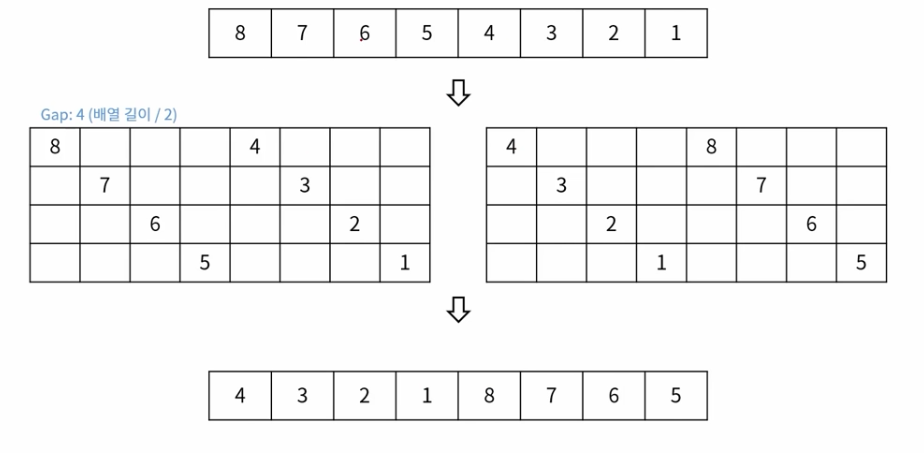
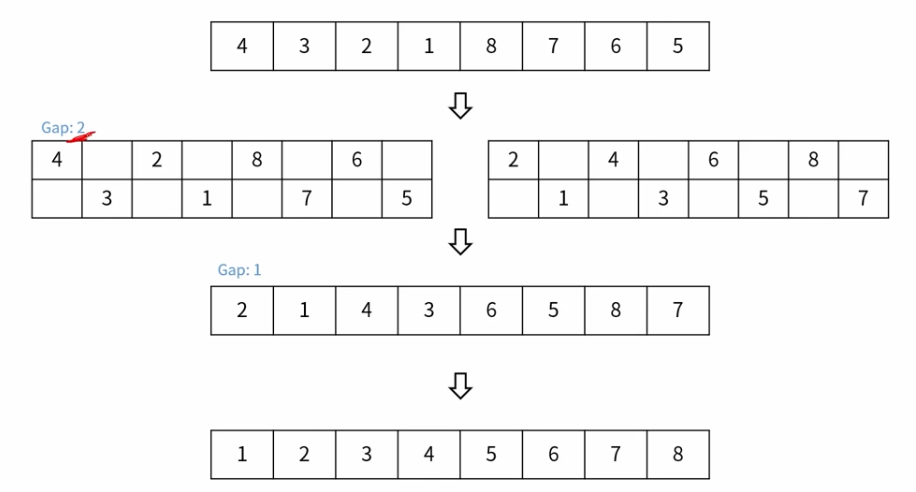
이후 갭은 초기 갭 / 2 형식으로 진행

정렬 알고리즘 복잡도 Summary

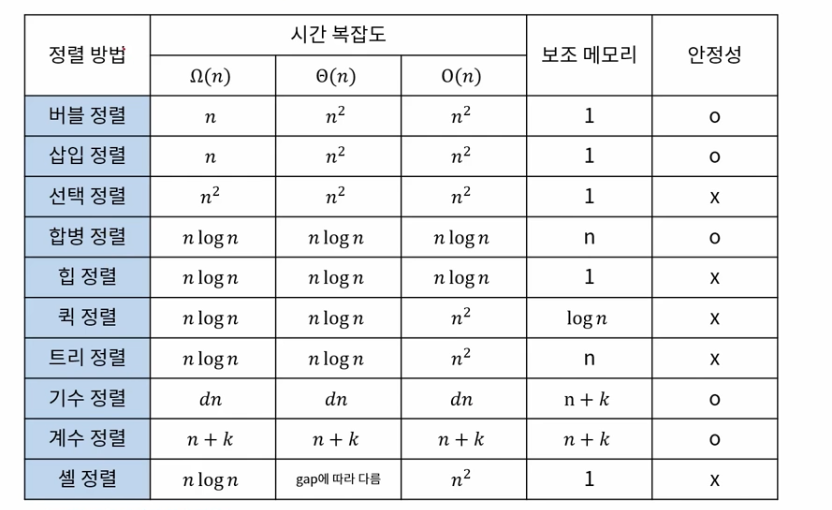
보조메모리가 1인 경우
-> swap할때 tmp 변수 하나 쓰는경우, 인플레이스 정렬 방식
-> 메모리를 추가로 사용하지 말라할때 사용하자

안정성 예시 예를들어

타입 1의 5, 3,타입 2의 5, 1
-> 이런식으로 숫자가 있다고 가정할때 예를들어 선택 정렬의 경우는 타입1의 5와 타입2의 5의 값은 같지만 서로 위치가 바뀔수 있다(기존의 순서 유지 여부)

---

RadixSort 구현

public class Main4 {
    public static void radixSort(int[] arr) {
        ArrayList<Queue<Integer>> list = new ArrayList<>();

        for (int i = 0; i < 10; i++) {
            list.add(new LinkedList<>());
        }

        int idx = 0;
        int div = 1;
        int maxLen = getMaxLen(arr);

        for(int i = 0; i < maxLen; i++) {
            for (int j = 0; j < arr.length; j++) {
                list.get((arr[j] / div) % 10).offer(arr[j]);
            }

            for (int j = 0; j < 10; j++) {
                Queue<Integer> queue = list.get(j);

                while (!queue.isEmpty()) {
                    arr[idx++] = queue.poll();
                }
            }

            idx = 0;
            div *= 10;
        }
    }

    public static int getMaxLen(int[] arr){
        int maxLen = 0;
        for(int i = 0; i < arr.length; i++){
            int len = (int)Math.log10(arr[i]) + 1; // 자릿수 구하는 법
            if(maxLen < len){
                maxLen = len;
            }
        }
        return maxLen;
    }

    public static void main(String[] args) {
        int[] arr = {10,32,52,27,48,17,99,56};
        radixSort(arr);
        System.out.println("기수 정렬 : " + Arrays.toString(arr));
    }
}

CountingSort 구현 예시

public class Main5 {
    public static void countingSort(int[] arr){

        int max = Arrays.stream(arr).max().getAsInt();
        int[] cntArr = new int[max + 1];

        for(int i = 0; i < arr.length; i++){
            cntArr[arr[i]]++;
        }

        int idx = 0;
        for (int i = 0; i < cntArr.length; i++) {
            while(cntArr[i] > 0){
                arr[idx++] = i;
                cntArr[i] -= 1;
            }
        }
    }

    public static void main(String[] args) {
        int[] arr = {10,32,10,27,32,17,99,56};
        countingSort(arr);
        System.out.println("계수 정렬 : " + Arrays.toString(arr));
    }
}

Shell Sort 구현 예시

public class Main6 {

    public static void shellSort(int[] arr){
        int gap = arr.length / 2;

        for(int g = gap; g > 0; g/=2){
            for (int i = g; i < arr.length; i++) {
                int temp = arr[i];

                int j = 0;
                for(int j = i - g; j >= 0; j -= g){
                    if(arr[j] > temp){
                        arr[j+g] = arr[j];
                    }else{
                        break;
                    }
                }
                arr[j+g] = temp;
            }
        }
    }
}

---