큐에 대해 자세히 알아보기!(선형 자료구조)

큐(Queue)

선입선출(FIFO) 자료구조

입력 순서대로 데이터 처리가 필요할 때 사용
-> 프린터 출력 대기열, BFS(Breath-First Search)등

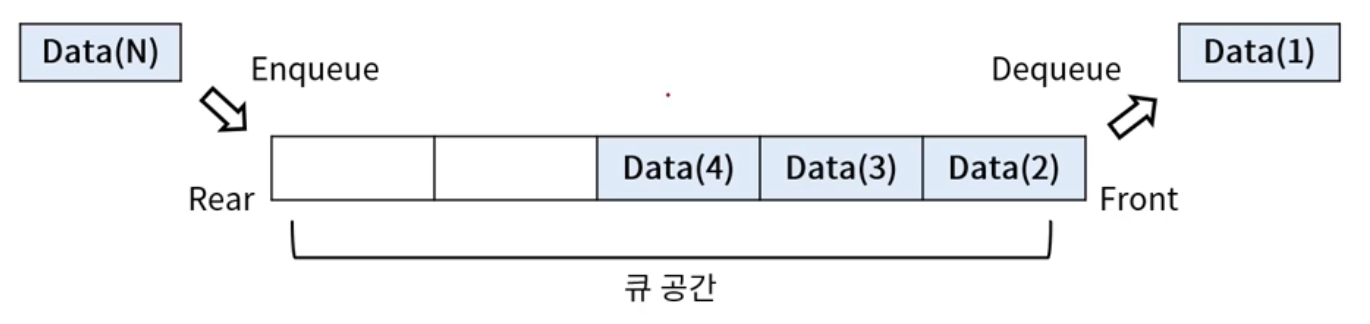
front(데이터 Dequeue 하는 쪽),rear(데이터 Enqueue 하는 쪽)

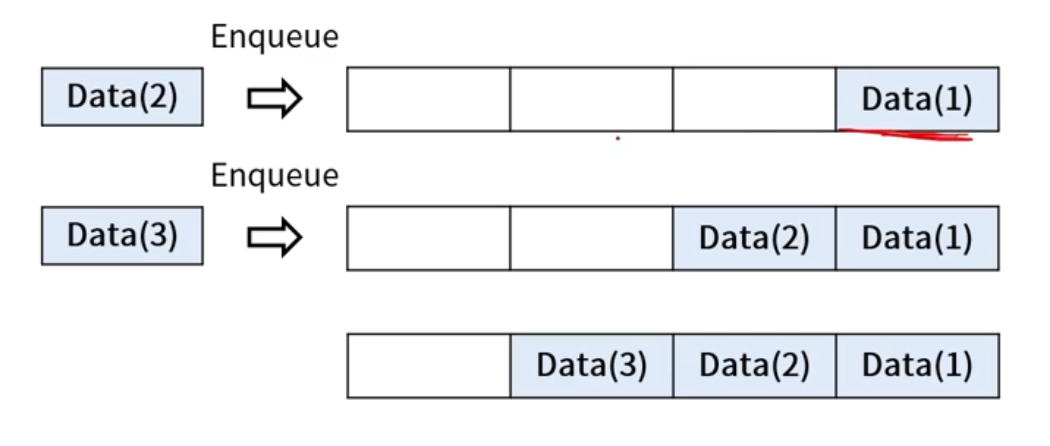
큐 클래스 이용해보기

public class Main {
    public static void main(String[] args) {
        // 큐의 경우는 인터페이스이기 때문에 Queue queue = new Queue()로 할경우 구현해야 할 것이 많음
        // LinkedList에 큐에 필요한 연산들이 구현되어져 있어서 사용(다형성)

        Queue queue = new LinkedList();

        queue.add(1);
        queue.add(2);
        queue.add(3);
        queue.add(4);
        queue.add(5);
        System.out.println(queue);

        System.out.println(queue.poll()); // pop과 같은 메서드
        System.out.println(queue); // [2,3,4,5]

        System.out.println(queue.peek()); // 2
        System.out.println(queue.contains(3));
        System.out.println(queue.size());
        System.out.println(queue.isEmpty());

        queue.clear();
        System.out.println(queue);
        System.out.println(queue.poll()); // Stack에서는 예외가 발생하는 반면, Queue에서는 null 반환

    }
}

ArrayList로 큐 구현해보기

class MyQueue1{
    ArrayList list;

    MyQueue1(){
        this.list = new ArrayList();
    }

    public boolean isEmpty(){
        return this.list.size() == 0? true : false;
    }

    public void push(int data){
        this.list.add(data);
    }

    public Integer pop(){
        if(this.isEmpty()){
            System.out.println("Queue is Empty!");
            return null;
        }
        int data = (int) this.list.get(0);
        this.list.remove(0);
        return data;
    }

    public Integer peek(){
        if(this.isEmpty()){
            System.out.println("Queue is Empty!");
            return null;
        }
        return (int)this.list.get(0);
    }
    
    public void printQueue(){
        System.out.println(this.list);
    }
}

배열로 큐 구현해보기(원형 큐)

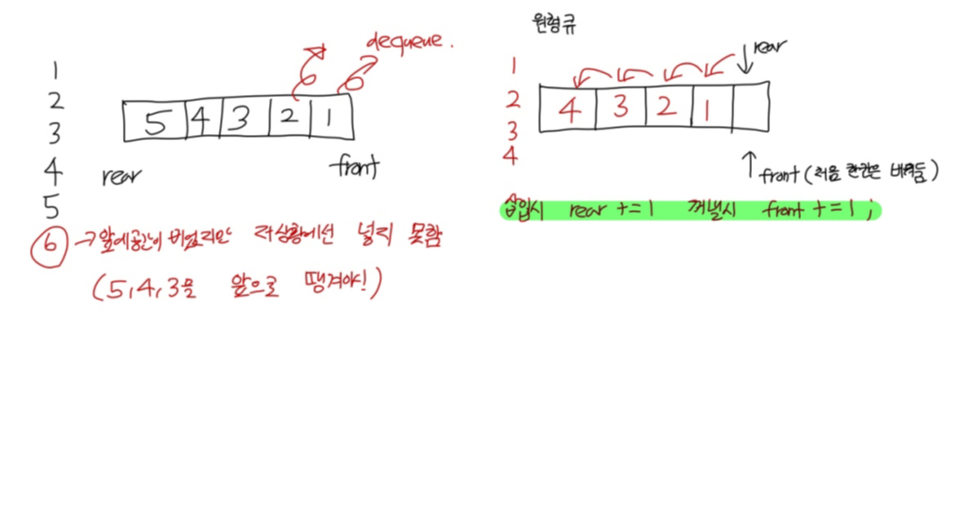
class MyQueue2{
    int[] arr;
    int front = 0;
    int rear = 0;

    MyQueue2(int size){
        arr = new int[size+1]; // front 한칸을 위해
    }

    public boolean isEmpty(){
        return this.rear == this.front;
    }

    public boolean isFull(){
        return (this.rear + 1) % this.arr.length == this.front;
    }

    public void enqueue(int data){
        if(this.isFull()){
            System.out.println("queue is Full!");
            return;
        }

        this.rear = (this.rear + 1) % this.arr.length;
        this.arr[this.rear] = data;
    }

    public Integer dequeue(){
        if(this.isEmpty()){
            System.out.println("queue is Empty!");
            return null;
        }
        front = (front+1) % this.arr.length; // front가 맨 뒤에 있을 경우를 대비한것!
        return this.arr[front];
    }

    public void printQueue(){
        int start = (this.front + 1) % this.arr.length;
        int end = (this.rear + 1) % this.arr.length;

        for(int i = start; i!= end; i = (i+1) % this.arr.length){
            System.out.print(this.arr[i] + " ");
        }
    }

}

연습문제

문제1 : 카드 섞기

// 카드 섞기
// 1~N까지의 번호로 구성된 N장의 카드가 존재
// 이때 1번 카드가 가장 위에 그리고 N번 카드는 가장 아래의 상태로 카드가 순서대로 쌓여있다.
// 아래의 동작을 카드 한장만 남을떄 까지 반복했을 때, 가장 마지막 남는 카드 번호를 출력
// 1. 가장 위의 카드는 버린다
// 2. 그 다음 위의 카드는 쌓여 있는 카드의 가장 아래에 다시 넣는다.

// 예시 N = 4 -> 결과 : 4
// N = 7 -> 결과 : 6
public class Practice3 {
    public static int findLastCard(int N){
        Queue queue = new LinkedList();

        IntStream.range(1,N+1).forEach(x-> queue.add(x));

        while(queue.size() > 1){
            queue.remove();
            queue.add((int) queue.remove());
        }

        return (int) queue.remove();
    }

    public static void main(String[] args) {
        System.out.println(findLastCard(4));
        System.out.println(findLastCard(7));
        System.out.println(findLastCard(9));
    }
}

문제2 : 요세푸스 문제

// 요세푸스 문제
// N과 K가 주어졌을 때 (N,K) 요세푸스 순열을 구하시오.
// N과 K는 N >= K를 만족하는 양의 정수
// 1부터 N번까지 N명이 순서대로 원을 이루어 모여 있다.
// 이 모임에서 원을 따라 순서대로 k번째 사람을 제외한다.
// 모든 사람이 제외될 떄까지 반복하며, 이 때, 제외되는 순서가 요세푸스 순열이다.

// 예시 입력
// N = 5, K = 2 -> 결과 : 2, 4, 1, 5, 3
// N = 7, K = 3 -> 결과 : 3, 6, 2, 7, 5, 1, 4

public class Practice4 {

    public static ArrayList getJosephusPermutation(int N, int K){
        ArrayList answer = new ArrayList();
        Queue queue = new LinkedList();

        IntStream.rangeClosed(1,N).forEach(x -> queue.add(x));

        int cnt = 0;
        while(!queue.isEmpty()){
            int data = (int)queue.remove();
            cnt += 1;

            if(cnt % K == 0){
                answer.add(data);
            }else{
                queue.add(data);
            }
        }
        return answer;
    }

    public static void main(String[] args) {
        System.out.println(getJosephusPermutation(5,2));
        System.out.println(getJosephusPermutation(7,3));
    }

}