[백준] 1967번 트리의 지름 ★

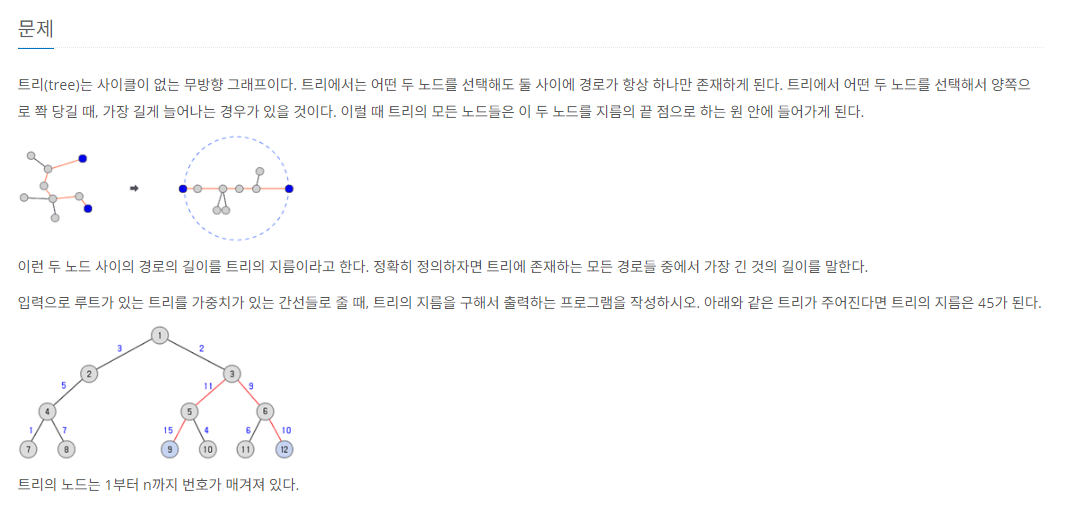
💡문제접근

• 처음에는 DFS를 이용해서 가장 깊은 노드를 탐색해 가장 최댓값이 나오는 노드를 하나 고르고 해당 노드에서부터 다시 DFS를 이용해서 가장 깊은 노드를 찾아 나오는 값이 트리의 지름이라고 생각해서 구현했는데 구현 과정에서 조금 애를 먹어 BFS로 방향을 바꿔 접근했다.

💡코드1(메모리 : 35348KB, 시간 : 88ms)

📌BFS(너비 우선 탐색)을 이용한 풀이 방식1

from collections import deque
import sys
input = sys.stdin.readline

n = int(input())
graph = [[] for _ in range(n+1)]
for _ in range(n-1):
    a, b, c = map(int, input().strip().split())
    graph[a].append([b, c])
    graph[b].append([a, c])

# 시작점, 누적합, 배열
def BFS(start, prefix_sum, result):
    queue = deque()
    queue.append([start, prefix_sum])
    while queue:
        s, p = queue.popleft()
        for i in graph[s]:
            node, cost = i
            if result[node] == -1:
                queue.append([node, cost])
                result[node] = cost + result[s]
    return result

result = [-1] * (n+1)
result[1] = 0
BFS(1, 0, result)
num = result.index(max(result))

result = [-1] * (n+1)
result[num] = 0
BFS(num, 0, result)
print(max(result))

💡코드2(메모리 : 36996KB, 시간 : 92ms)

📌DFS(깊이 우선 탐색)을 이용한 풀이 방식2

import sys
input = sys.stdin.readline
sys.setrecursionlimit(10 ** 6)

n = int(input())
graph = [[] for _ in range(n+1)]
for _ in range(n-1):
    a, b, c = map(int, input().strip().split())
    graph[a].append([b, c])
    graph[b].append([a, c])

def DFS(start, prefix_sum, result):
    for i in graph[start]:
        node, cost = i
        if result[node] == -1:
            result[node] = prefix_sum + cost
            DFS(node, prefix_sum + cost, result)
    return result

result = [-1] * (n+1)
result[1] = 0
DFS(1, 0, result)
num = result.index(max(result))

result = [-1] * (n+1)
result[num] = 0
DFS(num, 0, result)
print(max(result))

💡소요시간 : 57m