DFS(Depth First Search)

• 그래프 탐색의 한 종류로 깊이 우선 탐색이라고 함
• 루트 노드가 임의의 노드에서 시작하여 최대로 진입할 수 있는 깊이까지 탐색한 후 돌아와 다른 노드로 탐색하는 방식
• 'Stack'을 사용하여 데이터를 탐색
  • 재귀 함수를 이용해 Stack을 이용하는 경우가 많은 거 같다.

DFS 장단점

장점

1. 현 경로상의 노드들만 기억하면 되므로 저장공간 수요가 비교적 적음
2. 목표 노드가 깊은 단계에 있을 경우 해를 비교적 빨리 구할 수 있음

단점

1. 해가 없는 경로가 깊을 경우 탐색시간이 오래 걸릴 수 있음
2. 얻어진 해가 최단 경로가 된다는 보장이 없음

DFS의 흐름

전제 조건
1. 1번 정점을 root 노드로 하여 1번부터 탐색을 시작한다.
2. 번호가 작은 정점부터 탐색한다.

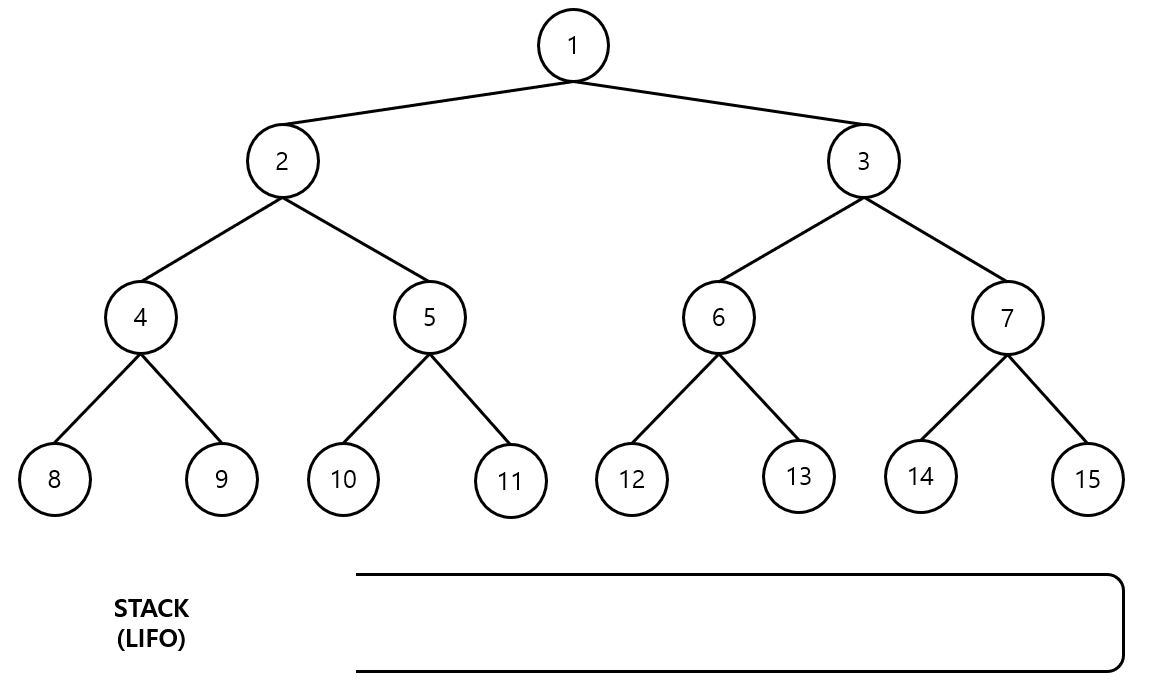
탐색 전 그래프

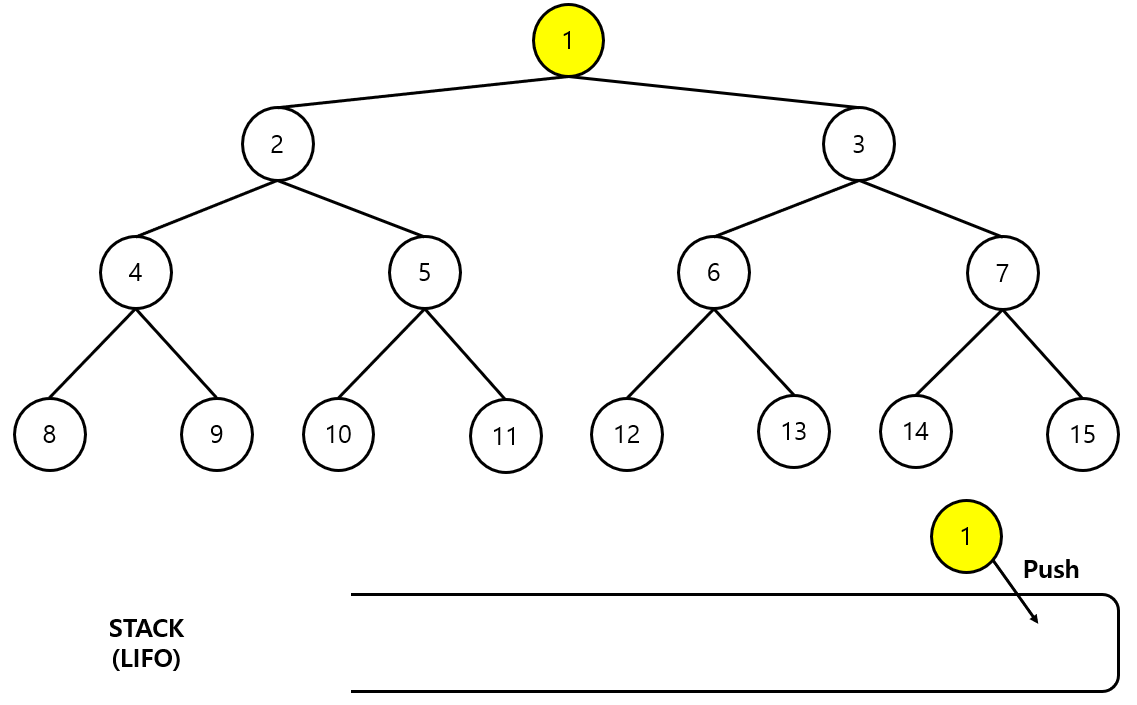
1단계

• 1번 노드를 스택에 추가하고 탐색할 노드가 있는 지 확인한다.

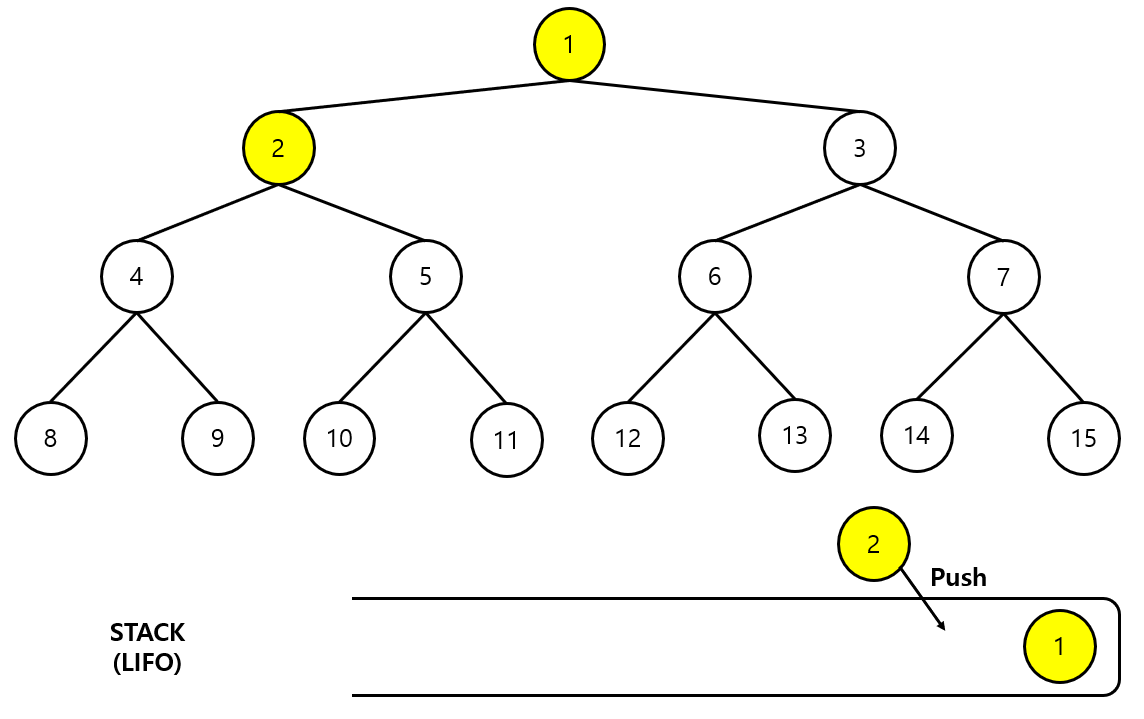
2단계

• 정점 번호가 작은 거 먼저 탐색하기로 했으므로 2번과 3번 중 2번을 스택에 추가한다.

3단계

• 2단계와 같은 방식으로 4번과 8번 정점을 스택에 추가한다.

4단계

• 8번 정점에서는 더 이상 추가할 정점이 없으므로 8번 노드를 스택에서 제거한다.
• 다시 4번 정점으로 가서 추가할 다른 정점이 있는 지 확인한다.
• 방문하지않은 9번 노드가 있으므로 9번 노드를 스택에 추가한다.

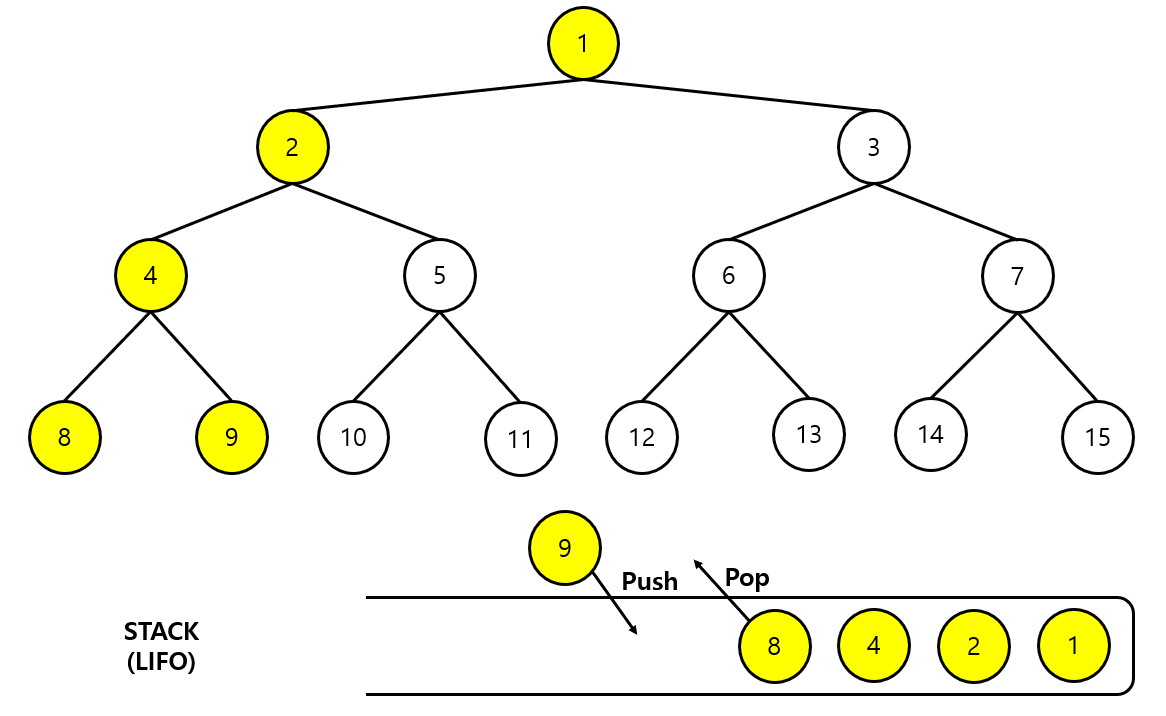
5단계

• 4단계와 동일하게 9번, 4번 정점은 더 이상 추가할 정점이 없으므로 스택에서 제거한다.
• 2번 정점에서 추가할 다른 정점이 있는 지 확인한다.
• 방문하지않은 5번 노드가 있으므로 5번 노드를 스택에 추가한다.

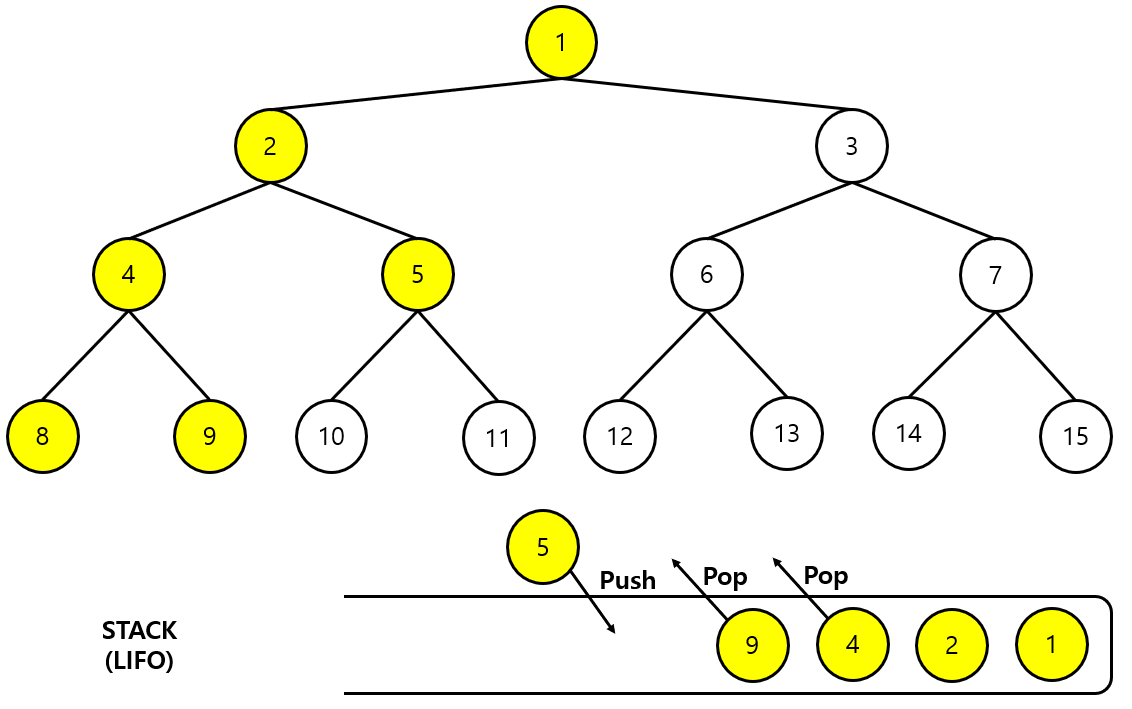
6단계

• 3단계와 4단계의 방법으로 진행한다.
  • 10번 정점을 스택에 추가한다.
  • 더 이상 추가할 정점이 없으므로 10번 정점을 스택에서 제거한다.
  • 5번 노드로 돌아가 추가할 다른 정점이 있는 지 확인한다.
  • 방문하지않은 11번 노드가 있으므로 11번 노드를 스택에 추가한다.

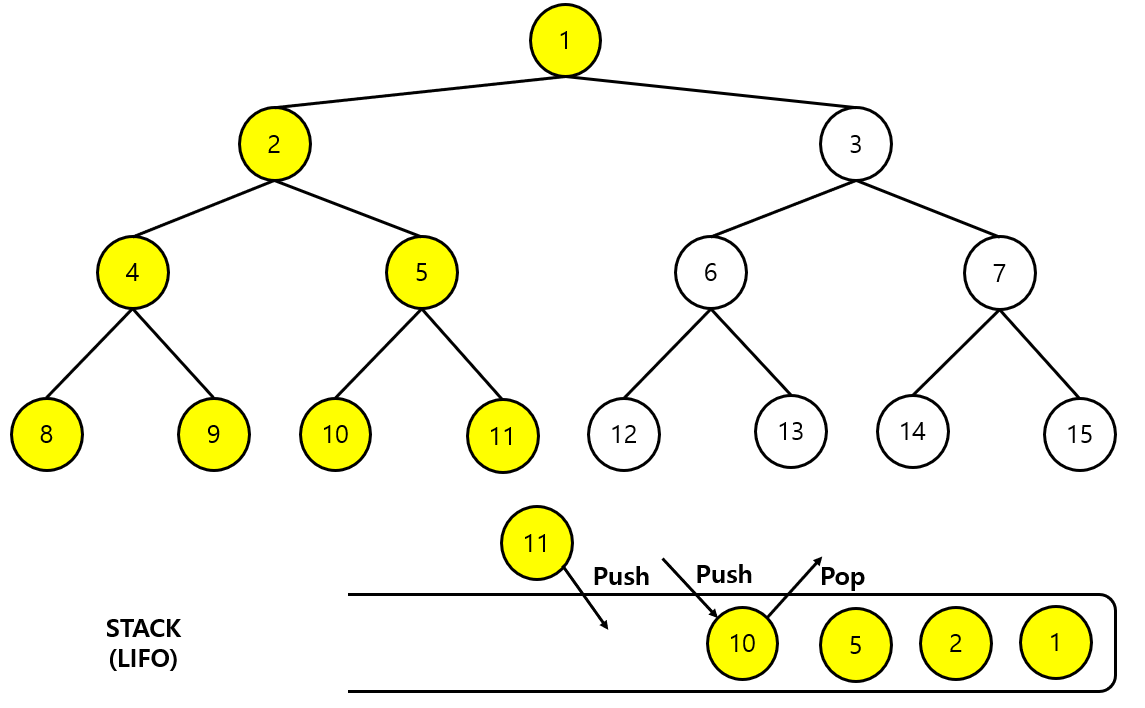
7단계

• 더 이상 추가할 정점이 없으므로 11번,5번,2번 정점을 스택에서 제거하고 1번 정점까지 돌아간다.
• 1번 정점에서 추가할 정점이 있는 지 확인한다.
• 3번 노드가 있으므로 3번 노드를 스택에 추가한다.
• 3단계 부터의 내용을 반복해 그래프를 탐색한다.

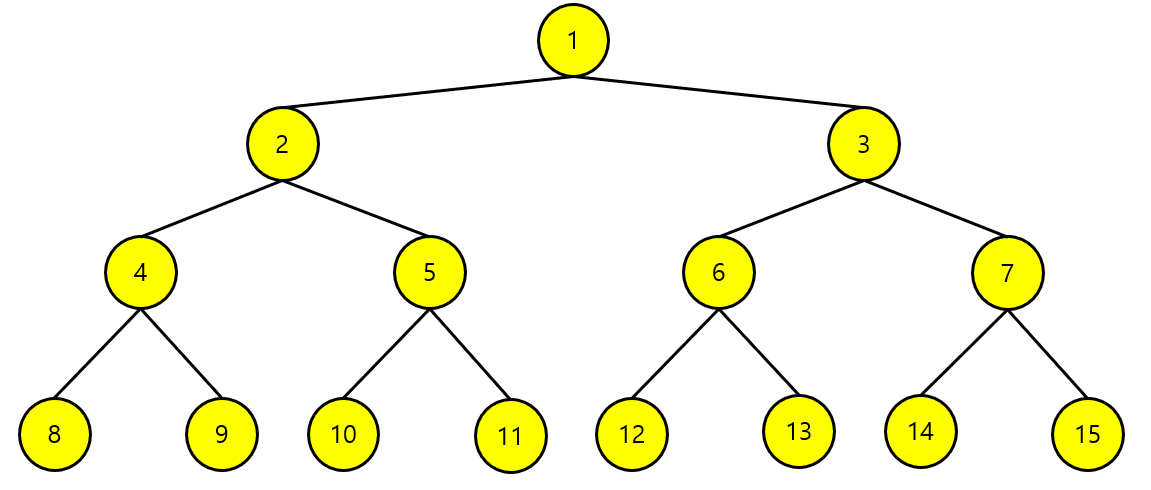
탐색 결과

• 탐색된 정점 순서 : 1->2->4->8->9->5->10->11->3->6->12->13->7->14->15
• 스택에서 제거되는 순서 : 8->9->4->10->11->5->2->12->13->6->14->15->7->3->1

DFS 구현 방법

1. 탐색을 시작할 정점을 스택에 추가한다.
2. 추가한 정점과 연결되어 있고 방문하지 않은 정점 중 하나를 스택에 추가(재귀 호출)한다.
3. 추가할 정점이 없을 때까지 2번을 반복한다.
4. 추가할 정점이 없다면 스택에서 정점을 꺼내며 상위 깊이의 정점으로 이동한다.
5. 그래프에서 방문하지 않은 정점이 없을 때까지 2,3,4를 반복한다.

그래프를 구현하는 2가지 방법으로 BFS 구현하기

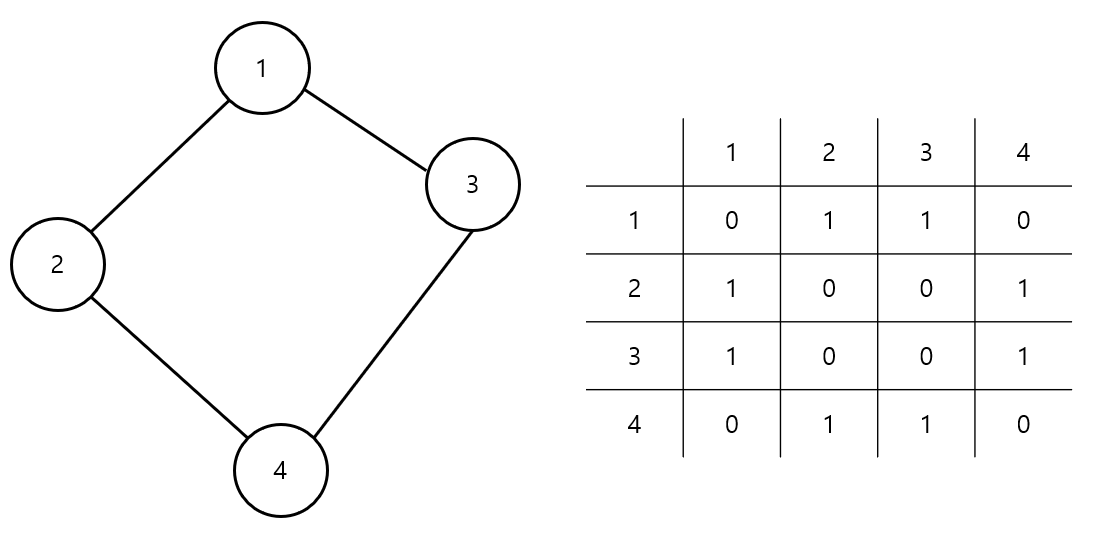
인접 행렬(Adjacency Matrix)

• 행렬을 이용해 정점들 사이의 관계를 표현
  • 보통 2차원 배열로 표현한다.
  • 노드^2 만큼의 공간을 차지하므로 정점의 수가 적거나 간선의 수가 많을 경우 사용
• 간선 방향의 존재 유무에 따라 표현하는 방법에 차이가 있음
• 가중치가 있다면 간선 존재 유무 칸에 가중치를 적어주면 된다.

DFS 중요 코드

• 2차원 배열 기반의 코드
• 재귀호출로 종단 지점까지 방문

public class dfs {

    static int edge;        // 간선의 수
    static int vertex;       // 정점의 수
    static int[][] map;     // 정점 간의 연결 정보를 담는 객체
    static boolean[] visit;   // 정점을 방문했는지 체크하기 위한 객체

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        vertex = sc.nextInt();
        edge = sc.nextInt();
        map = new int[vertex + 1][vertex + 1];
        visit = new boolean[vertex + 1];

        for (int i = 0; i < edge; i++) {
            int start = sc.nextInt();
            int next = sc.nextInt();

			// 여기가 중요!!! 정점 연관관계 저장
            map[start][next] = 1;
            map[next][start] = 1;
        }

        dfs(1);
    }

    public static void dfs(int start) {
        visit[start] = true;
        System.out.println(start + " ");

        for (int i = 1; i < vertex; i++) {
            if(!visit[i] && map[start][i] == 1)
                dfs(i);
        }
    }
}

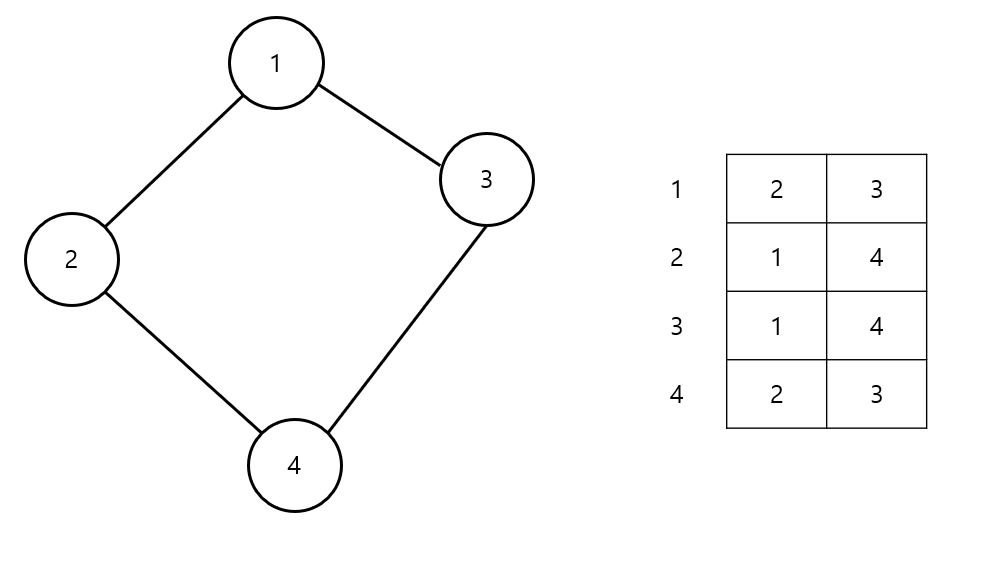
인접 리스트

• 각 정점이 연결된 노드들의 정보를 저장
• 간선 방향의 존재 유무에 따라 출발지 도착지를 고려하여 리스트에 정보 저장
  • 주로 ArrayList나 LinkedList로 구현
  • 정점이 많을 경우, 간선이 적을 경우 사용하면 인접 행렬보다 공간적 이득을 봄

public class dfs {
    static ArrayList<Integer>[] arrayList;				//	정점 간의 관계를 담는 객체
    static boolean[] visit;								// 정점을 방문했는 지 확인하는 객체
    ArrayList<Integer> dfsList = new ArrayList<>();		// 출력용 객체

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int vertex = sc.nextInt();
        int line = sc.nextInt();
        int startVertex = sc.nextInt();

        arrayList = new ArrayList[vertex + 1];
        visit = new boolean[vertex + 1];

        for (int i = 0; i < arrayList.length; i++) {
            arrayList[i] = new ArrayList<>();
        }

        for (int i = 0; i < line; i++) {
            int x = sc.nextInt();
            int y = sc.nextInt();

			// 여기가 중요!!! 정점 연관관계 저장
            arrayList[x].add(y);
            arrayList[y].add(x);
        }


        //  작은 수 부터 방문하도록 정렬
        for (int i = 1; i < vertex + 1; i++) {
            Collections.sort(arrayList[i]);
        }

        dfs(startVertex);

        for (Integer integer : dfsList) {
            System.out.print(integer + " ");
        }
    }

    public static void dfs(int x){
        if(visit[x])
            return;

        visit[x] = true;
        dfsList.add(x);
        for (int y : arrayList[x]) {
            if(!visit[y])
                dfs(y);
        }
    }
}

썸네일 출처

Pixabay로부터 입수된 mohamed Hassan님의 이미지 입니다.