
1. 어렵다 어려워 알고리즘..😫
알고리즘의 풀이를 보다보면 가끔 시간 복잡도란 단어 또는 O(N) 이렇게 생긴 문자를 보게된다.
이미 알고리즘을 풀다 지쳐서 풀이를 찾아보는데 비전공자인 내가 저 둘을 만나면 '머리야 궁금해 하지마.. 그냥 난 못본거야..'를 혼자 되뇌인다ㅋㅋㅋ🥲
하지만 이제는 양심에 찔려 시간복잡도에 대해서 정리를 하고 넘어가고자 한다.
2. 시간 복잡도란?🧐
시간 복잡도는 기본적인 연산을 수행하는데에 어떤 고정된 시간이 걸릴 때, 알고리즘에 의해서 수행되는 기본 연산의 개수를 세어 예측할 수 있다. 그러므로 걸리는 시간의 총량과 알고리즘에 의해 수행되는 기본적인 연산의 개수는 최대 상수 인자만큼 다르다. -위키피디아, 시간복잡도
따라서 시간 복잡도는 연산의 개수의 최대 상수의 인자로 알고리즘의 효율성을 판단하는 기준이라고 볼 수 있겠다.
3. 시간 복잡도의 종류
시간 복잡도는 크게 O(빅오), Ω(오메가), Θ(쎄타) 라고 불리는 3가지의 표기법을 가지고 있다. 이 중에 주로 빅오 표기법을 이용하여 복잡도를 표기한다. 그러므로 우리는 빅오 표기법에 대해서만 알아보겠다!🙂
4. 빅오 표기법
빅오 표기법은 점근적 상한을 의미한다. 쉽게 말하자면 최악의 경우에 걸리는 시간을 표기하는 방법이다.
O(1), O(logN), O(N), O(N*logN), O(N^2), O(N^3), ..., O(2^N), O(N!)
빅오 표기법은 위와 같이 표기한다.
보통 위의 시간 복잡도 중에 O(1)부터 O(N\*logN)까지는 괜찮은 알고리즘의 시간 복잡도이고, O(N^2)부터는 안 좋다고 생각하면 될 것이다.
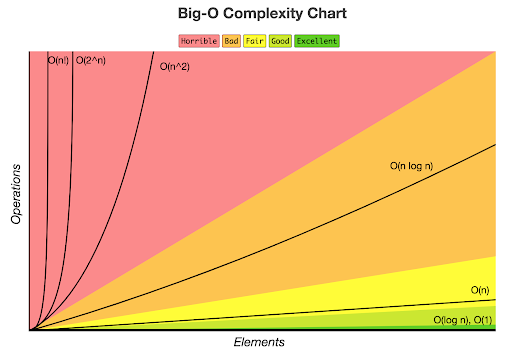
👆위의 차트를 보면 좀 더 시각적으로 이해가 될 것이다.
O(N^2)부터는 요소가 늘어날수록 연산의 횟수가 기하급수적으로 늘어난다.
그러므로 안 좋은 시간 복잡도를 갖고 있다면 요소가 적다면 괜찮을지 몰라도 요소가 늘어나면 기하급수적으로 늘어나는 연산 횟수를 감당하지 못하게 될 것이다.
4. 시간 복잡도 계산 방법
단순 계산
let sum = (N + 1) * N / 2;위의 코드는 (N+1)에서 한 번, * N에서 한 번, / 2에서 한 번, 대입 연산이 한 번 합쳐서 총 4번의 연산이 수행되었다.
빅오표기법으로 표현하면 4 = O(1) 이므로, 위 코드의 시간 복잡도는 O(1)이다.
let sum = 0;
for (let i=1; i <= N; i++)
sum += i;두번째 코드는 sum=0에서 한 번, int i=1에서 한 번, i++에서 N번, sum+=i에서 N번 합쳐서 총 2N+2 번의 연산이 수행된다.
2N+2의 최대 차항을 계수 없이 표기하면 N이므로 빅오표기법으로 표현하면 O(N)이다.
반복문 안의 반복문
let sum = 0;
for (let i = N; i > 0; i /= 2)
for (let j = 0; j < i; j++)
sum += j;코드는 바깥쪽 반복문이 logN번 반복하고, 안쪽 반복문은 i의 값에 따라 반복 횟수가 다르다.
i는 N부터 1까지 변하며, 안쪽 반복문은 해당하는 i만큼 반복하므로, N + N/2 + N/4 + … + 1 = 2N 번 반복하고, 빅오표기법으로 표기하면 2N = O(N)이다.
let sum = 0;
for (let i = 0; i < N; i++)
for (let j = 0; j < i; j++)
sum += j;바깥쪽 반복문은 N번 반복하고, 안쪽 반복문은 i의 값에 따라 반복 횟수가 다르다.
i는 0부터 N-1까지 변하며, 안쪽 반복문은 해당하는 i만큼 반복하므로, 0+1+2+…+(N-1) = N*(N-1)/2 번 반복한다.
따라서 시간 복잡도는 N*(N-1)/2 = O(N²)이다.
5. 마치며
시간 복잡도... 참 어렵다...
문제를 풀기라도하면 다행인 나는 시간 복잡도를 자주 계산해보진 않겠지만 나중에 남이 푼 알고리즘을 보면서 "이건 시간복잡도가 O(N)이니 괜찮을 것 같네여~😉" 라고 아는 척하기 좋을 것 같다ㅎㅎㅎ
💡출처
👉https://www.zerocho.com/category/Algorithm/post/57ea2987fdea850015313534
👉https://medium.com/humanscape-tech/코드의-시간-복잡도-계산하기-b67dd8625966
👉https://ko.wikipedia.org/wiki/시간_복잡도
👉https://www.bigocheatsheet.com
