
서론
벌써 8월도 끝나갑니다. 올해가 4달밖에 남지 않았네요! 입추가 지나고 말복이 지나도 여전히 무더운 날씨입니다. (정말.. 밖에서 10분만 있어도 땀이 나네요,,)
날씨야 어찌되었든!! 저는 코딩테스트를 준비하며 세이노 멘토님@why_dev_says_no의 코딩테스트 챌린지를 참여하고있는데요, 해당 챌린지를 통해 다양한 유형의 백준 문제들을 꾸준히 풀고있습니다.
이번 주에 제가 풀게 된 문제는 DFS / BFS관련된 문제인데요, 문제를 풀면서 어떤 문제에 DFS를 적용하고, 어떤 문제에 BFS를 적용해야 효율적인지 감이 오지 않더라구요. 특히나 이 알고리즘은 삼성전자 등 주요 기업 코테에서 정~~말 많이 나오는 유형이기 때문에 이번 기회를 통해 DFS와 BFS의 개념을 확실하게 정리하면서 두 알고리즘을 비교하고, 어떤 알고리즘을 적용하면 좋을지에 대해 이야기해보겠습니다ㅎㅎ
DFS와 BFS의 기본 개념
DFS (Ddepth First Search)
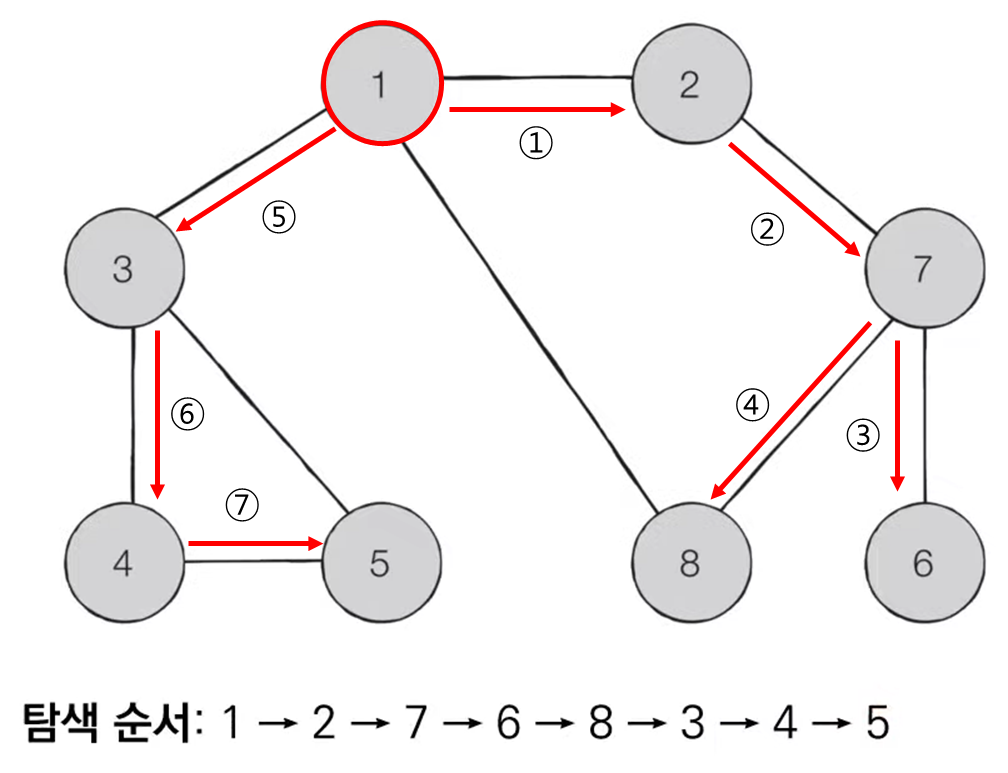
깊이 우선 탐색(DFS)은 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘입니다. 이 알고리즘은 특정한 경로로 탐색하다가 특정한 상황에서 최대한 깊이 들어가서 노드를 방문한 후, 다시 돌아가 다른 경로로 탐색하는 알고리즘입니다.
특징
- 스택 자료구조에 기초한다.
- 실제 구현에는 스택을 쓰지 않아도 되며 탐색을 수행함에 있어 데이터의 개수가 N개인 경우 O(N)의 시간이 소요된다.
동작 과정
- 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
- 스택의 최상단 노드에 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
- 2번 과정을 더 이상 수행할 수 없을 때까지 반복한다.
Tip. '방문 처리'는 스택에 한 번 삽입되어 처리된 노드가 다시 삽입되지 않게 체크하는 것을 의미한다. 방문 처리를 함으로써 각 노드를 한 번씩만 처리할 수 있다.
코드
#DFS메서드 정의
def dfs(graph, v, visited):
#현재 노드를 방문 처리
visited[v] = True
print(v)
#현재 노드와 연결된 다른 노드를 재귀적으로 방문
for i in graph[v]:
print("i", i)
if not visited[i]:
dfs(graph, i, visited)
graph = [[], [2, 3, 8], [1, 7], [1, 4, 5], [3, 5], [3, 4], [7], [2, 6, 8], [1, 7]]
#각 노드가 방문된 정보를 리스트 자료형으로 표현(1차원 리스트)
visited = [False] * 9
#정의된 dfs함수 호출
dfs(graph, 1, visited)BFS (Breathed First Search)
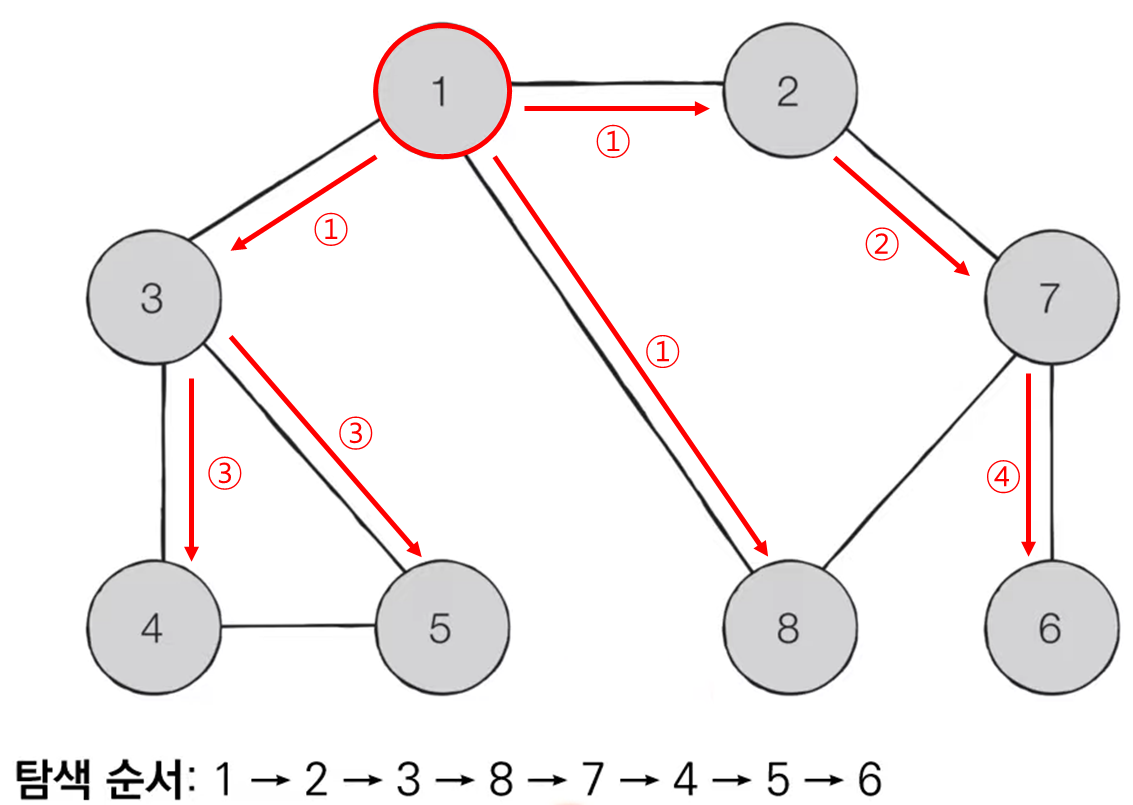
너비 우선 탐색(BFS)은 가까운 노드부터 탐색하는 알고리즘입니다. DFS가 최대한 멀리 있는 노드를 우선적으로 탐색하는 방식이라면 이 알고리즘은 그 반대입니다. BFS는 인접한 노드를 반복적으로 큐에 넣도록 알고리즘을 작성하면 자연스럽게 먼저 들어온 것이 먼저 나가게 되어, 가까운 노드부터 탐색을 진행하게 됩니다.
특징
- 선입 선출 방식인 큐 자료구조를 이용한다.
- 실제로 구현 시 deque라이브러리를 사용하는 것이 좋으며 탐색을 수행하는데 O(N)의 시간이 소요된다.
동작 과정
- 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
- 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 한다.
- 2번 과정을 더이상 수행할 수 없을 때까지 반복한다.
코드
from collections import deque
#BFS메서드 정의
def bfs(graph, start, visited):
#큐(queue) 구현을 위해 deque라이브러리 사용
queue = deque([start])
#현재 노드를 방문 처리
visited[start] = True
#큐가 빌때까지 반복
while queue:
#큐에서 하나의 원소를 뽑아 출력
v = queue.popleft()
print(v, end=' ')
#해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
for i in graph[v]:
if not visited[i]:
queue.append(i)
visited[i] = True
#각 노드가 연결된 정보를 리스트 자료형으로 표현(2차원 리스트)
graph = [[], [2, 3, 8], [1, 7], [1, 4, 5], [3, 5], [3, 4], [7], [2, 6, 8], [1, 7]]
#각 노드가 방문된 정보를 리스트 자료형으로 표현(1차원 리스트)
visited = [False] * 9
#정의된 BFS함수를 호출
bfs(graph, 1, visited)DFS / BFS 비교
| 내용 | 설명 | |
|---|---|---|
| 동작 원리 | 스택 | 큐 |
| 구현 방법 | 재귀 함수 이용 | 큐 자료구조 이용 |
DFS와 BFS의 효율성
DFS는 스택이나 재귀를 사용하여 구현되므로, BFS에 비해 메모리 사용량이 적을 수 있습니다. 그래서 경로의 가능성을 탐색하는 경우 유리하게 작용합니다.
하지만 DFS는 사이클이 있는 그래프에서는 무한 루프에 빠질 수 있으므로, 이를 방지하기 위한 추가적인 조치가 필요합니다. 왜냐하면 DFS는 탐색 과정에서 이미 방문한 노드를 다시 방문할 가능성이 있기 때문입니다.
BFS는 모든 노드를 방문하므로 완전 탐색 문제에 적합합니다. 특히, 최단 경로를 찾거나 레벨별 정보가 필요한 경우 BFS가 더 효율적입니다. 또한 특징에서 살펴보았듯이 BFS는 큐 자료구조에 기초한다는 점에서 deque라이브러리를 활용할 수 있어 구현할 수 있어서 구현이 간단한 편입니다.
재귀 함수로 DFS를 구현하면 컴퓨터 시스템의 동작 특성상 실제 프로그램의 수행 시간은 느려질 수 있습니다. 따라서 스택 라이브러리를 이용해 시간 복잡도를 완화하는 테크닉이 필요할 때도 있습니다.
👉 코딩테스트에서 보통은 DFS보다는 BFS 구현이 조금 더 빠르게 동작한다라는 정도로만 기억합시다!
적용 사례와 결정 요인
DFS는 모든 노드를 방문하기 때문에 모든 가능한 경로를 탐색하며 해결책을 찾는데 유용하고, BFS는 최단 경로 문제에 적합합니다.
알고리즘을 선택할 때에는 탐색해야 할 그래프의 크기, 사이클의 존재 유무, 메모리 사용량, 최단 경로 찾기의 필요성 등을 고려해야 합니다. 왜냐하면 이러한 요소들은 알고리즘의 효율성에 직접적인 영향을 미치기 때문입니다.
DFS로 전처리를 해줘야 하는 경우나 DFS를 이용하는 알고리즘이 아닌 단순히 그래프에서 모든 정점을 탐색하는 용도라면 DFS, BFS 중 편하신걸 사용하셔도 대부분의 문제는 해결이 가능할 것입니다.
단 여기서 주의할 점은 가중치 없는 그래프의 최단 경로문제는 BFS로만 접근해야 한다는 것입니다.
요약
- DFS: 미로 찾기, 퍼즐게임 등. 가능한 모든 경로를 탐색하며, 해결책을 찾을 때까지 깊이 탐색한다.
- BFS: 소셜 네트워크에서의 친구 추천, 최단 경로 찾기 등에 적합하다.
(BFS는 레벨별로 탐색하기 때문에 최단 거리를 보장하기 때문이다.)
결론
DFS와 BFS는 그래프 탐색에 있어 대표적인 두 가지 방법이며, 각각의 특성과 적용 사례를 이해하는 것이 중요합니다.
문제를 풀 때 적절한 알고리즘을 선택함으로써 우리는 문제를 보다 효율적으로 해결할 수 있습니다. 효율적으로 해결한다는 것은 메모리 사용을 최적화하고, 알고리즘의 실행시간을 단축시킬 수 있다는 의미입니다.
따라서, 문제를 푸는 경우 문제의 특성을 정확히 분석 후 각 알고리즘의 장단점을 고려하여 선택하는 것이 좋겠네요!!
그럼 이번 포스팅은 여기서 마치겠습니다.🙌
참고자료
