이번 포스팅에서는 이진 탐색 알고리즘과 이 알고리즘을 변형한 코드를 통해 Lower Bound와 Upper Bound의 개념을 알아보도록 하겠습니다.

알고리즘 소개

이진 탐색(Binary Search)이란?

오름차순으로 정렬된 리스트에서 특정한 값의 위치를 찾는 알고리즘. 이진 탐색은 모든 값을 탐색하는 일반 탐색과 달리 O(logN)의 시간복잡도를 갖기 때문에 정렬된 자료에 대해 빠른 탐색 속도를 갖습니다.

이진 탐색의 동작 방식

배열에서 이진 탐색의 동작 방식입니다.

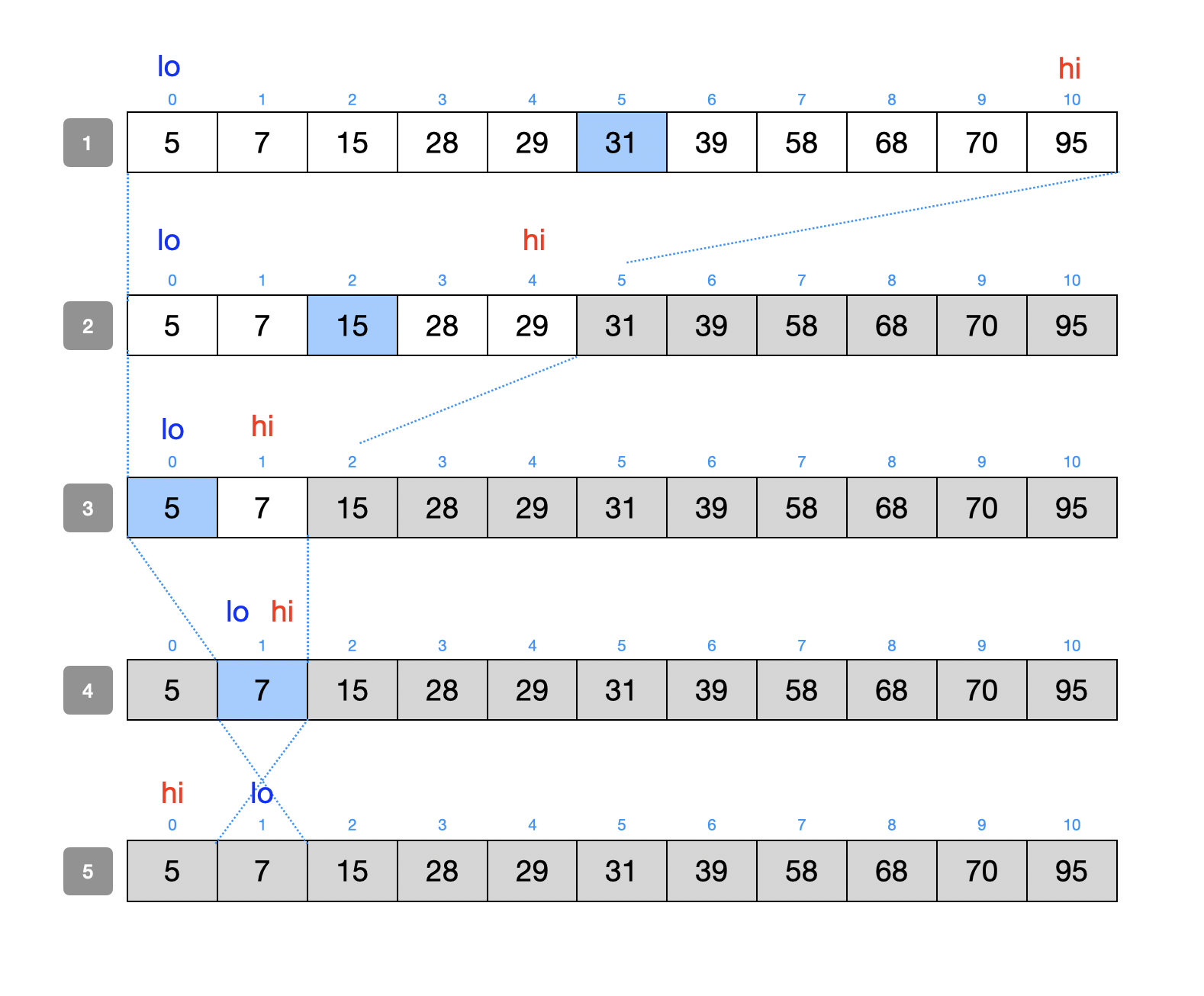
a. 정렬된 배열에서중간 인덱스를 찾습니다. 그림 1
b. 이후 찾으려는 값(val)와 중간 값(mid)을 비교합니다. 그림 1
c. val가 mid보다 작으면 mid를 기준으로 왼쪽 부분 배열을 탐색합니다. val가 mid보다 크면 mid를 기준으로 오른쪽 부분 배열을 탐색합니다. 그림 2
d. 탐색 범위가 더이상 없을 때까지 위 과정을 반복합니다. 그림 3, 4
e. lo가 hi보다 커지게 되면 탐색에 실패합니다. 그림 5

구현

동작 방식에 기초해서 코드로 구현해보도록 하겠습니다.

from typing import Any, Sequence

def binary_search(arr: Sequence, val: Any) -> int:
	lo = 0		# 검색 범위 맨 앞 원소의 인덱스
    hi = len(arr) - 1		# 검색 범위 맨 끝 원소의 인덱스
    
    while True:
    	mid = (lo + hi) // 2		# 중앙 원소의 인덱스
        if arr[mid] == val:
        	return mid		# 검색 성공
        elif arr[mid] < val:
        	lo = mid + 1	# 검색 범위를 뒤쪽 절반으로 좁힘
        else:
        	hi = mid - 1	# 검색 범위를 앞쪽 절반으로 좁힘
        if lo > hi:
        	break

이진 탐색 중 같은 값을 저장하는 요소가 여럿인 경우가 있을겁니다. 이 경우 이진 탐색을 조금 변형한 lower bound또는 upper bound를 사용해야 합니다.

Lower Bound

찾고자 하는 값(val)이 처음 나오는 위치를 의미합니다. 리스트 a를 정의하고 lower bound를 구하는 코드를 구현해보았습니다.

a = [1, 2, 3, 4, 4, 4, 5, 6, 7, 8] # n=10

def lower_bound(arr, val):
  lo = 0
  hi = len(arr) 
  while lo < hi:
    mid = (lo + hi)//2
    if arr[mid] < val:
      lo = mid+1
    else:
      hi = mid  
  return lo  # 결국 lo와 hi가 같아짐 
  
print(lower_bound(a, 4))	# 3  

lower_bound()를 이용하여 4가 가장 처음 나온 위치를 출력해 본 결과 인덱스 3이 잘 출력되는 것을 확인할 수 있습니다.

*참고: 위 코드에서 왜 hi = len(arr) - 1이 아니라 hi = len(arr)인지는 upper bound에서 설명하도록 하겠습니다.

Upper Bound

찾고자 하는 값이 여러개인 경우 마지막 위치의 다음 위치를 의미합니다.

a = [1, 2, 3, 4, 4, 4, 5, 6, 7, 8] # n=10

def upper_bound(arr, val):
  lo = 0
  hi = len(arr)
  while lo < hi:
    mid = (lo + hi)//2
    if arr[mid] <= val: # 같으면 그 값은 후보가 될 수 없음 -> lo = mid + 1
      lo = mid+1
    else:
      hi = mid  
  return lo  # 결국 lo와 hi가 같아짐 
  

print(upper_bound(a, 4))

lower bound와 upper bound를 활용하여 특정 원소의 갯수를 구할수도 있습니다.

print(upper_bound(a, 4) - lower_bound(a, 4))

코드 추가 설명

마치기 전에 lower bound에서 설명하지 않았던 부분에 대해 짚어봅시다. 위 코드에서 hi = len(arr) - 1이 아니라 hi = len(arr)인 이유는 뭘까요?

upper_bound()의 hi값만 len(arr) - 1로 수정하고 다음 코드의 결과를 예상해봅시다.

a = [1, 2, 3, 4, 4, 4, 5, 6, 7, 8] # n=10

def upper_bound(arr, val):
  lo = 0
  hi = len(arr) - 1
  while lo < hi:
    mid = (lo + hi)//2
    if arr[mid] <= val:
      lo = mid+1
    else:
      hi = mid  
  return lo  
  
print(upper_bound(a, 8)) # 9

위 코드의 출력 결과는 10이 나와야 하지만 9가 나옵니다. len(a)의 최댓값은 10이므로 hi(=len(a) - 1)의 최댓값은 9이기 때문입니다. 따라서 정상적적으로 출력되기 위해서는 len(arr)로 지정해주어야 합니다.

참고자료

[tistory] 이진탐색 백준 문제 추천 - jaewon_sss
[youtube] (백준 1920번, Class 2) 수 찾기 - 승욱은
Do it! 자료구조와 함께 배우는 알고리즘 입문 - 파이썬 편
[velog] 이분탐색 Lower Bound와 Upper Bound - eunseokim