[python/백준] 1010. 다리 놓기(S5)

📌 문제 탐색하기

👉 문제바로가기
T: 테스트 케이스 개수
N, M: 서쪽과 동쪽에 있는 사이트 개수(0 < N ≤ M < 30)

N이 M보다 작기 때문에 모든 N은 M개의 사이트와 하나씩은 연결이 됩니다. M개 중 N개를 뽑는 경우의 수를 구하면 되겠네요. 이 문제에서 다리끼리는 서로 겹쳐질 수 없다는 조건에 주목해봅시다. M개 중 N개를 뽑기만하면 x번째에 위치한 M의 사이트는 반드시 x번째에 위치한 N의 사이트와 연결되어야 다리가 서로 겹치지 않습니다.

📌 알고리즘

1️⃣ math.factorial()

M개중에서 N개를 뽑는 경우는 조합(combination) 개념을 활용할 수 있습니다. 다리끼리는 서로 겹쳐질 수 없기 때문에 M개 중 N개를 선택하기만하면 N개 중 어디와 연결되어야하는지 자동으로 결정됩니다. 따라서 순서에 상관 없으므로 순열이 아닌 조합을 활용합니다.

*math.factorial()을 활용하면 팩토리얼 값을 구할 수 있습니다.

2️⃣ DP

이 문제를 다이나믹 프로그래밍으로 해결할 수 있는지 생각해봅시다. 다이나믹 프로그래밍을 적용하려면 해당 문제가 작은 문제로 분해되는지, 작은 문제의 답을 다음 단계의 계산에서 활용할 수 있을지 생각해보면 됩니다.

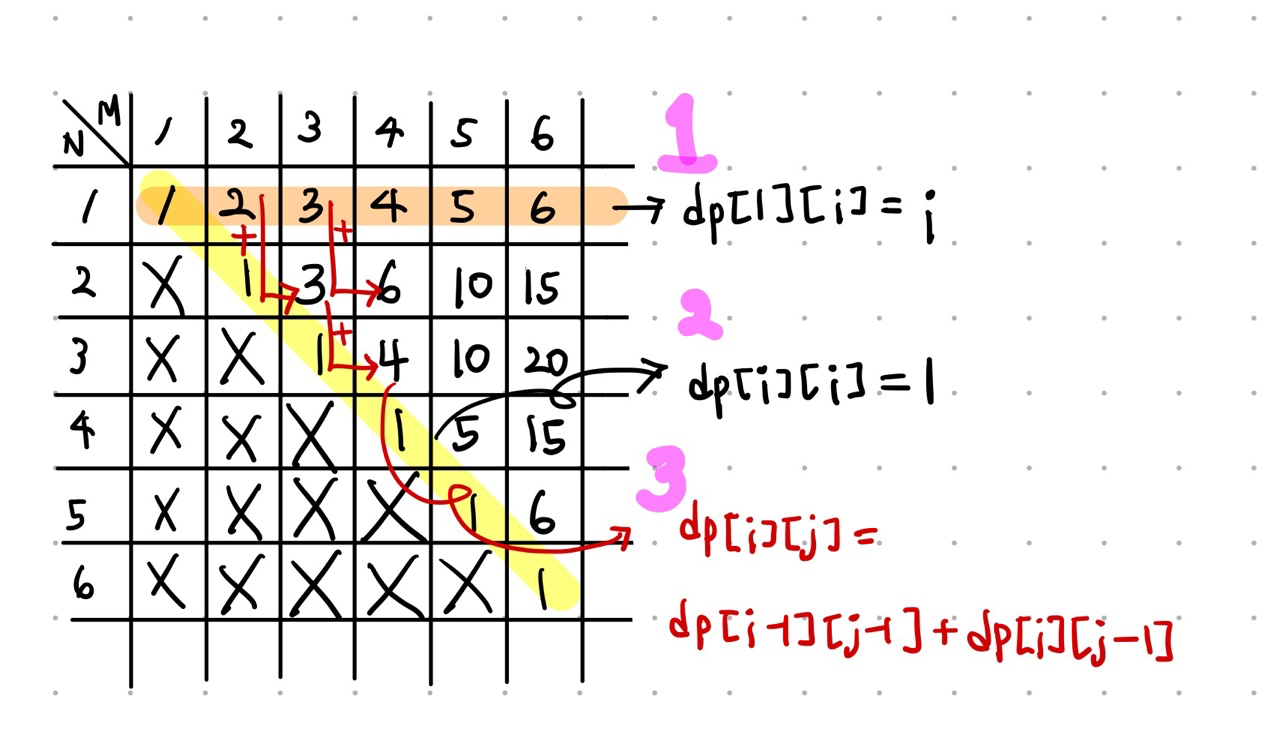
1. N이 1인 경우 다리의 수=M

• dp[1][i] = i

2. N과 M의 값이 같은 경우 N=M=다리의 수

• dp[i][i] = 1

3. 1, 2에 해당되지 않는 모든 경우

• dp[i][j] = dp[i-1][j-1] + dp[i][j-1]

위 그림을 통해 이전에 계산한 결과가 이후 값을 구하는 데 활용되기 때문에 다이나믹프로그래밍을 활용할 수 있겠네요.

시간복잡도

math.factorial()은 시간복잡도가 O(N)입니다. 테스트 케이스 수 만큼 반복해야 하므로 총 시간 복잡도는 O(T*N)이 됩니다. 만약 다이나믹 프로그래밍으로 해결하는 경우, 먼저 이중 for문의 시간복잡도는 O(N*M)입니다. 이중for문 또한 테스트 케이스 수 만큼 반복해야 하므로 총 시간 복잡도는 O(T*N*M)이 됩니다.

📌 코드 설계하기

1️⃣ math.factorial

1. 테스트 케이스 수(T)를 입력받습니다.
2. math.factorial()을 활용하여 결과값을 구한 후 출력합니다.

2️⃣ DP

1. 테스트 케이스 수(T)를 입력받습니다.
2. N, M의 2차원 리스트를 활용하기 위해 초기화해줍니다.
3. 각 케이스 별로 실행할 코드를 리스트에 대입합니다.
4. N행 M열의 값을 출력합니다.

📌 정답 코드

1️⃣ math.factorial

import sys
import math

T = int(sys.stdin.readline())   #테스트 케이스 수

for _ in range(T):
    N, M = map(int, sys.stdin.readline().split())

    result  = math.factorial(M) // (math.factorial(M-N) * math.factorial(N))
    print(result)

2️⃣ DP

import sys

T = int(sys.stdin.readline())
MAX_OF_M = 30

for _ in range(T):
    N, M = map(int, sys.stdin.readline().split())
    dp = [[0]*MAX_OF_M for _ in range(MAX_OF_M)]

    for i in range(1, M+1):
        dp[1][i] = i
        dp[i][i] = 1

    for i in range(2, N+1):
        for j in range(2, M+1):
            dp[i][j] = dp[i-1][j-1] + dp[i][j-1]        

    print(dp[N][M])