📌 문제 탐색하기
👉 문제바로가기
입력
T: 테스트 케이스의 개수
N: 순열의 크기(2 ≤ N ≤ 1,000)
순열: 각 정수는 공백으로 구분
순열의 크기를 지정하고 순열이 주어진 경우 순열 사이클의 개수를 구하는 문제입니다. 한 숫자를 지정했을 경우 해당 숫자와 연결된 모든 노드를 탐색해야 합니다.
우리가 구해야 하는 것은 사이클의 수이며 사이클마다 정점은 하나씩 존재합니다. 결론적으로 우리는 정점의 갯수를 구해주면 됩니다!!
문제에서 주어진 순열을 예시로 들어보면, 8개의 순열 (3, 2, 7, 8, 1, 4, 5, 6)이 있을 경우 배열을 이용해 다음과 같이 표현할 수 있습니다.
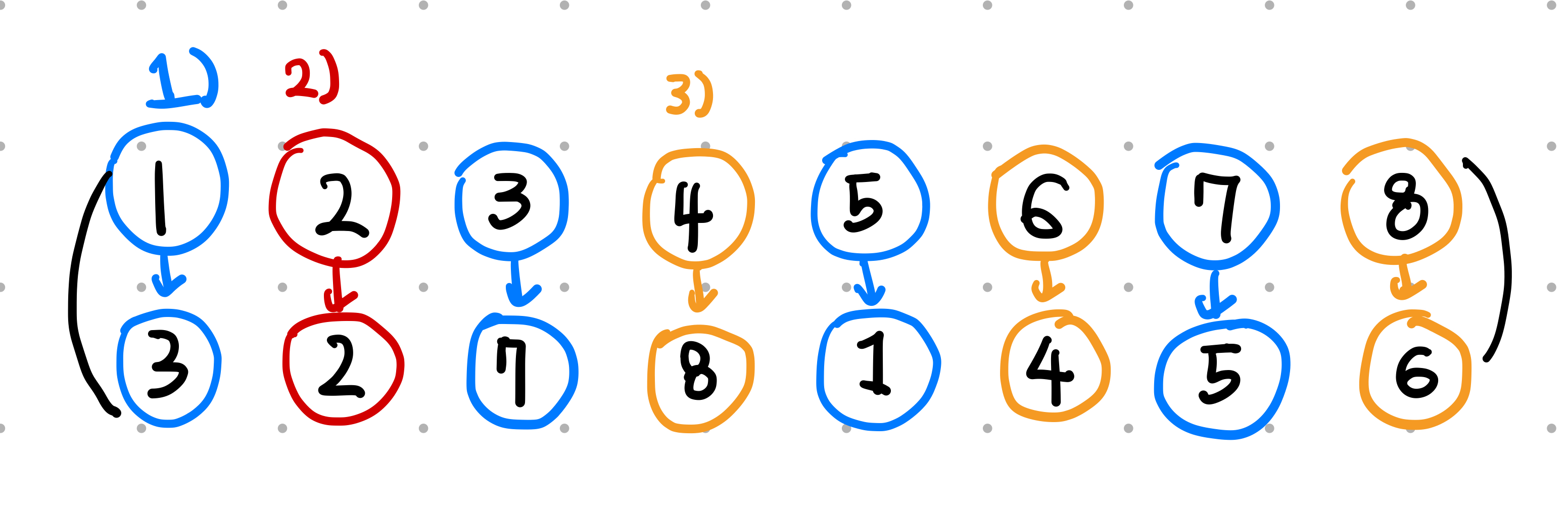
1) 1 → 3, 3 → 7, 7 → 5, 5 → 1
2) 2 → 2
3) 4 → 8, 8 → 6, 6 → 4
위 순서를 참고하여 그림으로 나타내면 다음과 같습니다.
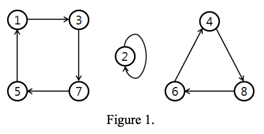
결국 1~8까지의 배열과 순열 (3, 2, 7, 8, 1, 4, 5, 6)를 하나씩 매치한 화살표가 노드와 노드의 연결을 의미합니다.
노드와 노드의 연결쌍을 알았으면 이전에 풀었던 문제들처럼 그래프를 기록할 수 있습니다.
1️⃣ 입력 및 변수 정의
먼저 테스트 케이스의 개수(T)와 순열의 크기(N)를 입력받습니다.
T = int(sys.stdin.readline()) #테스트 케이스 수
N = int(sys.stdin.readline()) #순열의 크기이후 순열의 크기만큼 순열을 입력받고 방문 횟수여부를 담은 리스트visited를 정의합니다.
arr2 = list(map(int, sys.stdin.readline().split())) #순열
visited = [False] * (N+1)
count = 0 #정점의 수arr1은 순열과 매치하기 위한 1~8까지의 숫자 리스트이기 때문에 반복문을 이용하여 1부터 순열의 크기만큼 숫자를 append해줍니다.
arr1 = []
for i in range(1, N+1):
arr1.append(i)2️⃣ 노드정보 저장 및 그래프 기록
1~8까지를 저장한 리스트 arr1과 8개의 수로 이루어진 순열을 저장한 리스트 arr2를 활용하여 노드와 노드의 연결 정보를 리스트newArray에 저장합니다.
newArray = [[] for _ in range(N)]
for i in range(N):
newArray[i].append(arr1[i])
newArray[i].append(arr2[i])저장된 노드 정보를 활용하여 인접리스트를 활용해 리스트graph에 기록합니다. 이때 해당 리스트의 중복을 제거하고, 작은 수부터 시작하도록 정렬하기 위해 sort()를 사용합니다.
graph = [[] for _ in range(N+1)]
for i in range(N):
graph[arr1[i]].append(arr2[i])
graph[arr2[i]].append(arr1[i])
#graph의 각 요소들을 정렬
for i in range(N+1):
graph[i] = list(set(graph[i])) #중복제거
graph[i].sort() 3️⃣ DFS함수 정의
def dfs(start):
visited[start] = True
#현재 노드와 연결된 다른 노드를 재귀적으로 방문
for i in graph[start]:
if not visited[i]:
dfs(i)4️⃣ 순열 사이클 개수 구하기
1부터 시작해서 아직 방문하지 않은 연결된 노드들을 방문합니다. 모두 탐색했으면 방문하지 않은 다른 숫자를 정점으로해서 반복합니다. 정점이 하나 정해질때마다 count하여 정점의 개수를 구하고 출력합니다.
for i in range(1, N+1):
if not visited[i]:
dfs(i)
count += 1
print(count) 📌 알고리즘 선택
한 시작점이 정해지면 해당 노드와 연결된 노드를 끝까지 다 탐색해야 하므로 DFS를 활용하여 풀 수 있습니다.
시간복잡도
- 그래프 구축:
O(N)- 중복 제거 및
sort()를 사용하여 정렬:O(NlogN)- dfs탐색:
O(N+E)
최악의 경우 시간복잡도를 구하기 위해 N의 최대값이 1000인 경우, 모든 노드가 다른 모든 노드와 연결된 경우를 고려합니다. 이경우 E는 최대 N이며 결론적으로 E=N=1000입니다. 따라서 전체 시간복잡도는 O(N)+O(NlogN)+O(N)=O(NlogN)=O(1000*log1000)입니다.
📌 코드 설계하기
- 테스트 케이스의 개수(T)와 순열의 크기(N)를 Input받습니다.
- 노드의 정보를 저장하고 해당 정보를 활용해 그래프를 기록합니다.
- DFS를 수행하면서 정점의 개수를 구하고 출력합니다.
📌 정답 코드
import sys
def dfs(start):
visited[start] = True
#현재 노드와 연결된 다른 노드를 재귀적으로 방문
for i in graph[start]:
if not visited[i]:
dfs(i)
T = int(sys.stdin.readline()) #테스트 케이스 수
for _ in range(T):
N = int(sys.stdin.readline()) #순열의 크기
arr1 = []
arr2 = list(map(int, sys.stdin.readline().split())) #순열
visited = [False] * (N+1)
count = 0 #정점의 수
for i in range(1, N+1):
arr1.append(i)
newArray = [[] for _ in range(N)]
for i in range(N):
newArray[i].append(arr1[i])
newArray[i].append(arr2[i])
graph = [[] for _ in range(N+1)]
for i in range(N):
graph[arr1[i]].append(arr2[i])
graph[arr2[i]].append(arr1[i])
#graph의 각 요소들을 정렬
for i in range(N+1):
graph[i] = list(set(graph[i])) #중복제거
graph[i].sort()
for i in range(1, N+1):
if not visited[i]:
dfs(i)
count += 1
print(count) 
