[python/백준] 11742. 연결 요소의 개수(S2)

📌 문제 탐색하기

👉 문제바로가기

• N: 정점의 개수(1 ≤ N ≤ 1,000)
• M: 간선의 개수(0 ≤ M ≤ N×(N-1)/2)
• u, v: 간선의 양 끝점(1 ≤ u, v ≤ N, u ≠ v)

노드와 노드의 쌍이 주어진 경우 연결 요소의 개수를 구하는 문제입니다.

주어진 예제를 예시로 들어보겠습니다.

• 노드는 6개이며, 간선은 5개입니다.
• 1과 2가 연결되어 있습니다.
• 2와 5가 연결되어 있습니다.
• 5와 1이 연결되어 있습니다.
• 3과 4가 연결되어 있습니다.
• 4와 5가 연결되어 있습니다.

위 정보를 그림으로 그려보면 아래와 같습니다.

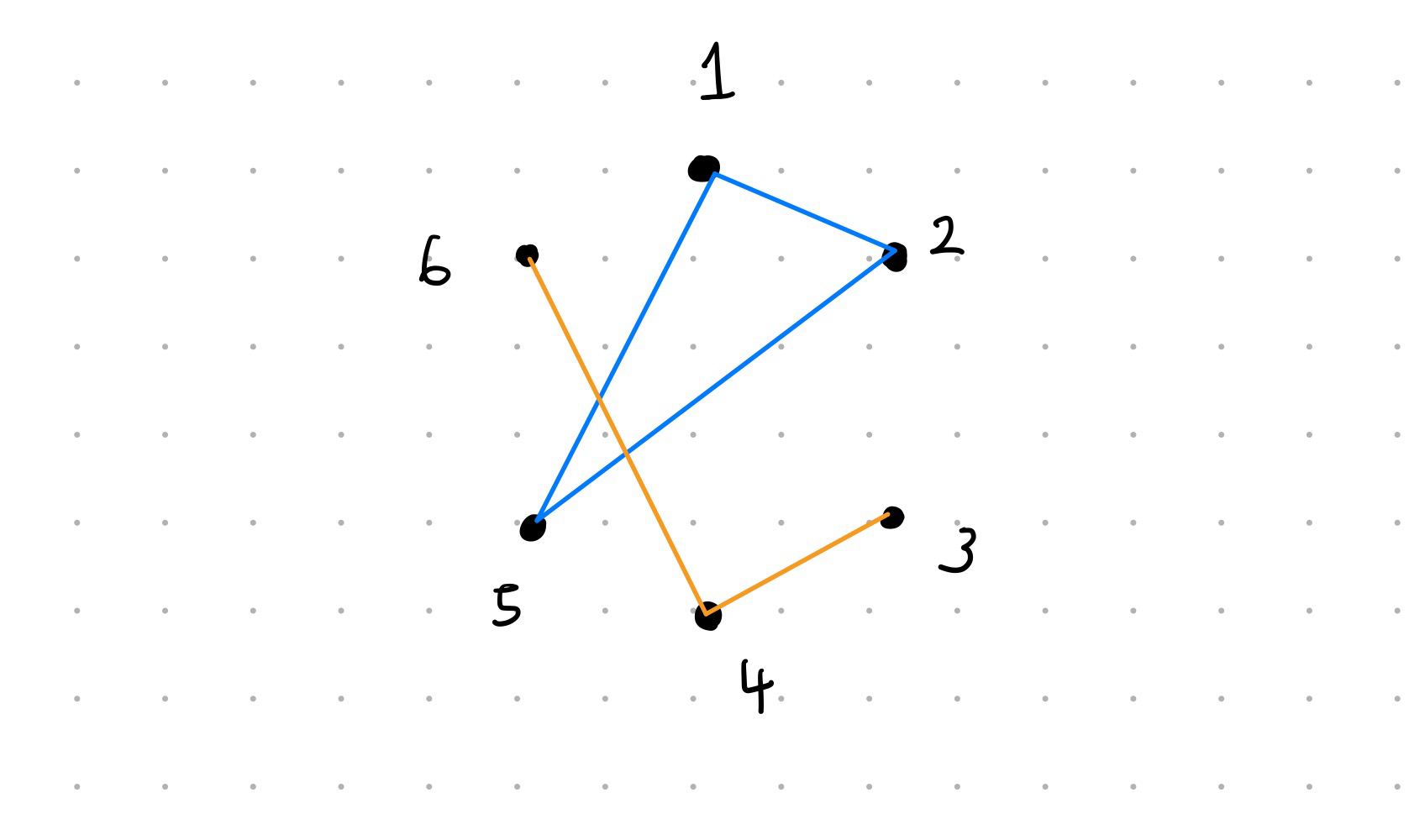
그림에서 볼 수 있듯이 1-2-5가 연결되어 하나의 요소를 이루고, 6-4-3이 연결되어 하나의 요소를 이룹니다.

이 문제를 보자마자 몇일 전 풀어보았던 순열 사이클 문제가 생각났습니다. (상당히 유사한 방법으로 풀 수 있겠네요ㅎㅎ)

요소의 개수를 구한다는 것은 한 점을 정점으로 선택하고 해당 점과 연결된 모든 노드들을 탐색해나가는 과정에서, 선택된 정점의 개수를 count한다는 의미로 해석하면 되겠네요.

결국 우리가 구해야 할 것은 정점의 개수입니다!!

1️⃣ 입력 및 변수 정의

먼저 정점의 개수(N)과 간선의 개수(M)를 공백을 사이에 두고 입력받습니다. 그래프 구축 전 그래프 리스트를 초기화하고 방문 여부를 담을 리스트도 정의합니다.

N, M = map(int, sys.stdin.readline().split())
graph = [[] for _ in range(N+1)]  #그래프 리스트 초기화
visited = [False] * (N+1)
count = 0

2️⃣ 노드정보 저장 및 그래프 기록

노드-노드 쌍을 공백을 사이에 두고 입력받은 후 인접리스트 방법으로 그래프에 저장합니다.

for _ in range(M):
    a, b = map(int, sys.stdin.readline().split())
    graph[a].append(b)
    graph[b].append(a)

3️⃣ DFS함수 정의

def dfs(v):
    visited[v] = True
    for i in graph[v]:
        if not visited[i]:
            dfs(i)

4️⃣ 연결 요소의 개수 구하기

1부터 시작해서 정점으로 잡고 연결된 모든 노드를 방문하며 dfs()를 수행합니다. 연결된 노드가 더이상 없을 경우 다른 정점을 찾아 dfs()를 다시 수행합니다. 정점을 하나 찾을 때 마다 count를 1씩 증가시킵니다.

for i in range(1, N+1):
    if not visited[i]:
        dfs(i)
        count += 1

📌 알고리즘 선택

한 점을 정점으로 선택하고 해당 점과 연결된 모든 노드들을 모두 탐색하면 되기 때문에 DFS를 활용할 수 있겠네요.

시간복잡도

• 그래프 구축: O(M)
• dfs탐색: O(N+M)

최악의 경우 DFS는 모든 노드와 간선을 정확히 한 번 방문합니다. 따라서 전체 시간복잡도는 O(N+M)입니다. N의 최댓값은 1000이고, M의 최댓값은 (1,000*999)/2이므로 약 500,000입니다. 따라서 연산은 최대 약 501,000번 수행되므로 주어진 시간 내에 충분히 가능한 연산입니다.

📌 코드 설계하기

1. N, M값과 노드-노드 쌍을 입력받습니다.
2. 노드 연결정보를 통해 그래프 리스트를 구축합니다.
3. DFS를 수행합니다.

📌 정답 코드

import sys

sys.setrecursionlimit(10000)

def dfs(v):
    visited[v] = True
    for i in graph[v]:
        if not visited[i]:
            dfs(i)

N, M = map(int, sys.stdin.readline().split())
graph = [[] for _ in range(N+1)]  #그래프 리스트 초기화
visited = [False] * (N+1)
count = 0

for _ in range(M):
    a, b = map(int, sys.stdin.readline().split())
    graph[a].append(b)
    graph[b].append(a)

for i in range(1, N+1):
    if not visited[i]:
        dfs(i)
        count += 1

print(count)