이분 탐색

둘로 나누어 찾는 값이 있을 법한 곳만 탐색하는 방법

둘로 나누어서 탐색을 진행하기 때문에 순차탐색보다 원하는 자료를 훨씬 빨리 찾을 수 있다. 순차탐색과 다른 점은 정렬되어 있는 리스트를 다룬다는 점이다.

이분 탐색의 원리

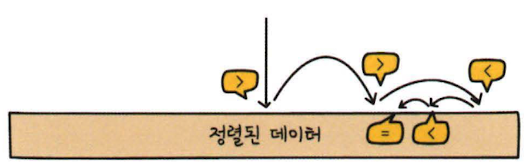
1. 중간 위치를 찾는다.
2. 찾는 값과 중간 위치 값을 비교한다.
3. 같다면 원하는 값을 찾은 것이므로 위치 번호를 결괏값으로 돌려준다.
4. 찾는 값이 중간 위치 값보다 크다면 중간 위치의 오른쪽을 대상으로 다시 탐색한다. (1번 과정부터 반복)
5. 찾는 값이 중간 위치 값보다 작다면 중간 위치의 왼쪽을 대상으로 다시 탐색 한다. (1번 과정부터 반복)
   

알고리즘

# 리스트에서 특정 숫자 위치 찾기(이분 탐색)
# 입력: 리스트 arr, 찾는 값 n
# 출력: 찾으면 그 값의 위치, 찾기 못하면 -1

def binary_search(arr, n):
    # 탐색할 범위를 저장하는 변수 start, end
    # 리스트 전체를 범위로 탐색 시작(0 ~ len(a) -1)

    start = 0
    end = len(arr) -1
    
    while start <= end:             # 탐색할 범위가 남아 있는 동안 반복
        mid = (start + end) // 2    # 탐색 범위의 중간 위치
        if n == arr[mid]:           # 발견 !
            return mid
        elif n > arr[mid]:          # 찾는 값이 더 크면 오른쪽으로 범위를 좁혀 계속 탐색
            start = mid + 1
        else:                       # 찾는 값이 더 작으면 왼쪽으로 범위를 좁혀 계속 탐색
            end = mid - 1

    return -1                       # 찾지 못했을 때

알고리즘 분석

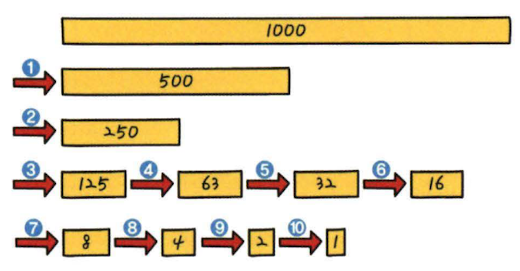
이분 탐색은 값을 비교할 때마다 찾는 값이 있을 범위를 절반씩 좁히면서 탐색하는 효율적인 탐색 알고리즘이다.
순차 탐색의 최악의 경우에 자료 천 개와 모두 비교해야 하지만, 이분 탐색은 최악의 경우에도 자료 열 개와 비교하면 탐색을 마칠 수 있다. (log 1,000 ≈ 9.966)

이분 탐색의 계산 복잡도는 O(log n) 으로, 순차 탐색의 계산 복잡도인 O(n) 보다 훨씬 더 효율적이다.

이분 탐색을 가능하게 하려면 자료를 미리 정렬해 둬야 해서 번거로울 수 있지만 필요한 값을 여러 번 찾아야 한다면 시간이 조금 걸리더라도 자료를 한 번 정렬한 다음에 이분 탐색을 계속 이용하는 방법이 훨씬 효율적이다.