LCS
최장 공통 부분 수열(LCS)는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제입니다.
LCS의 길이를 구하는 방법
LCS의 길이는 다음과 같은 점화식으로 다이나믹 프로그래밍을 사용해 구할 수 있습니다.
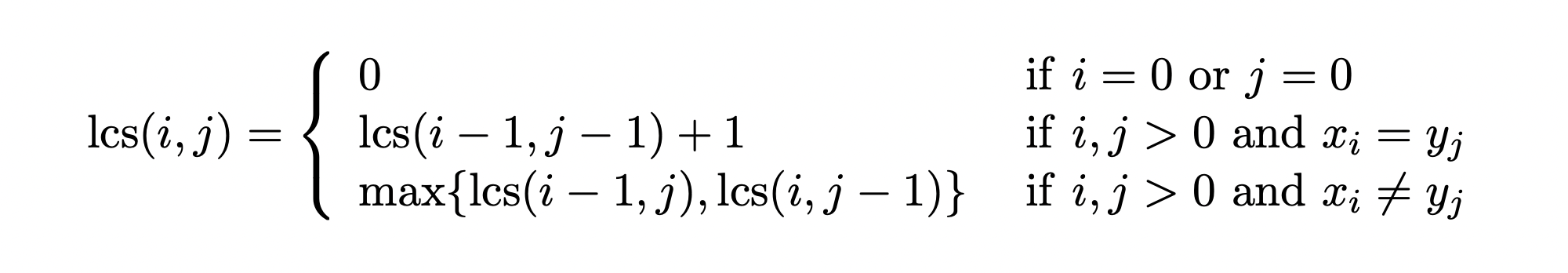
구하는 과정은 여기에서 자세히 살펴볼 수 있습니다.
이를 코드로 구현해보면 다음과 같습니다.
void LCS(std::string x, std::string y)
{
int m = x.length();
int n = y.length();
int dp[m + 1][n + 1];
std::memset(dp, 0, sizeof(dp));
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (x[i - 1] == y[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = std::max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
std::cout << dp[m][n];
}걸리는 시간은 이 됩니다.
실제 LCS를 구하는 방법
LCS의 길이뿐만 아니라 직접 LCS를 구할 수도 있습니다.
구현하는 과정은 여기에서 살펴볼 수 있습니다.
이를 코드로 구현해보면 다음과 같습니다.
void LCS(std::string x, std::string y)
{
int m = x.length();
int n = y.length();
int dp[m + 1][n + 1];
std::memset(dp, 0, sizeof(dp));
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (x[i - 1] == y[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = std::max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
std::cout << dp[m][n] << '\n';
int i = m;
int j = n;
std::string ans;
while (ans.length() != dp[m][n]) {
// up
if (dp[i - 1][j] == dp[i][j]) {
i--;
continue;
}
if (dp[i][j - 1] == dp[i][j]) {
j--;
continue;
}
ans += x[i - 1];
i--;
j--;
}
std::reverse(ans.begin(), ans.end());
std::cout << ans;
}LCS의 공간복잡도를 줄여보기
지금까지 LCS의 길이를 구하기 위해서 의 공간복잡도를 사용해 dp 배열을 채웠습니다.
하지만 구하는 과정을 살펴보면, dp 배열의 단 두 개 행만을 사용한다는 것을 알 수 있습니다.
따라서 두 개의 행만을 저장하며 진행하면 공간복잡도를 로 줄일 수 있습니다.
그런데 여기서 또 생각해보면, LCS의 길이를 구할 때 dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]만을 사용한다는 것을 알 수 있습니다.
따라서 의 공간복잡도로 구현할 수 있습니다.
void LCS(std::string& x, std::string& y)
{
int a = x.size();
int b = y.size();
// x를 더 긴 문자열로 설정한다.
if (a < b) {
std::swap(a, b);
std::swap(x, y);
}
std::vector<int> prev(b + 1);
for (int i = 1; i <= a; ++i) {
int prev_diag = 0;
for (int j = 1; j <= b; ++j) {
int temp = prev[j];
if (x[i - 1] == y[j - 1]) {
prev[j] = prev_diag + 1;
} else {
prev[j] = std::max(prev[j], prev[j - 1]);
}
prev_diag = temp;
}
}
std::cout << prev[b];
}Hirschberg
공간복잡도를 으로 줄이는 위 방법은 LCS의 길이는 구할 수 있지만 실제 LCS를 구하지는 못합니다.
왜냐하면 실제 LCS를 구하려면 전체 테이블이 필요하기 때문입니다.
이를 가능하게 하기 위해 Hirschberg 알고리즘을 사용합니다.
Hirschberg 알고리즘을 사용하면 시간과 공간으로 실제 LCS를 구할 수 있습니다.
오른쪽에서 왼쪽으로
지금까지는 왼쪽에서 오른쪽으로 살펴보며 LCS를 구했습니다.
하지만 이번에는 오른쪽에서 왼쪽으로 살펴보며 테이블을 채워보는 방법을 알아봅시다.
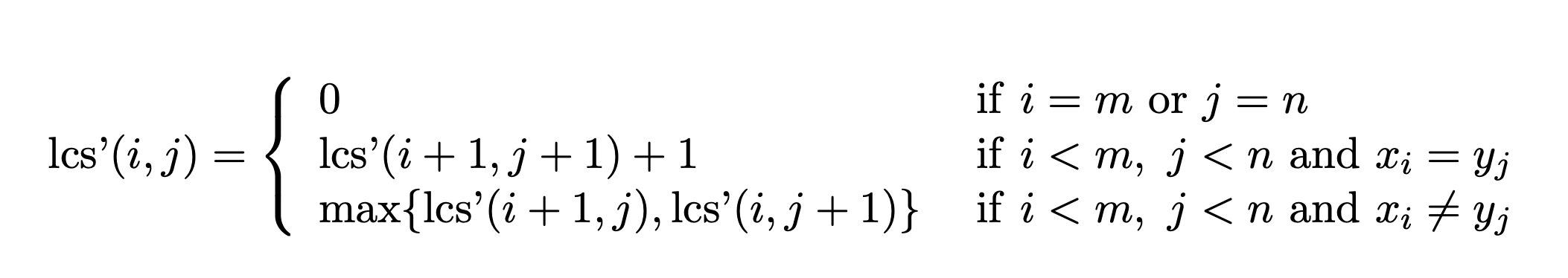
하지만 아직은 새로운 것을 구한 것은 아닙니다. 그저 다른 방향으로 테이블을 채운 것이죠.
분할 정복
Hirschberg의 아이디어는 분할 정복입니다.
문자열 X과 Y의 LCS를 S라고 해봅시다.
S의 문자들 중 일부는 X[1 .. m / 2]에 포함되고 나머지는 X[m / 2 + 1 .. m]에 포함될 것입니다.
그리고 이에 대응하는 Y를 두 부분으로 나눴을 때 Y[1 .. k]와 Y[k + 1 .. n]이라고 해봅시다.
그러면 결론적으로 S는 X[1 .. m / 2], Y[1 .. k]의 LCS와 X[m / 2 + 1 .. m], Y[k + 1 .. n]의 LCS를 합친 것이 됩니다.
이를 식으로 나타내면 다음과 같습니다.