서로소 집합과 크루스칼 알고리즘 - 백준 1197 (22.6.29)

서로소 집합

수학에서 서로소 집합이란 공통 원소가 없는 두 집합을 의미한다.

예를 들어 집합 {1,2}와 집합 {3,4}는 서로소 관계이다. 반면에 집합 {1,2}와 집합 {2,3}은 2라는 원소가 두 집합에 공통적으로 포함되어 있기 때문에 서로소 관계가 아니다.

서로소 집합 자료구조

서로소 집합 자료구조란 서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조이다. union, find연산으로 조작할 수 있다.

find 연산

#특정 원소가 속한 집합 찾기
def find(parent, x):
    #루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀호출
    if x != parent[x]:
        return find(parent, parent[x])
    return parent[x]

find 함수를 재귀적으로 호출한 뒤에 부모 테이블값을 갱신하는 경로 압축 기법 적용

def find(x):
    if x != parent[x]:
        parent[x] = find(parent[x])
    return parent[x]

union(합집합) 연산

# 두 원소가 속한 집합을 합치기
def union(parent, a, b):
    a = find(a)
    b = find(b)
    if a > b:
        parent[b] = a
    else:
        parent[a] = b

크루스칼 알고리즘

크루스칼 알고리즘(Kruskal Algorithm)을 사용하면 가장 적은 비용으로 모든 노드를 연결할 수 있다. 그리디 알고리즘으로 분류된다.

먼저 모든 간선에 대하여 정렬을 수행한 뒤에 가장 거리가 짧은 간선부터 집합에 포함시키면 된다. 이때 사이클을 발생시킬 수 있는 간선의 경우, 집합에 포함시키지 않는다.

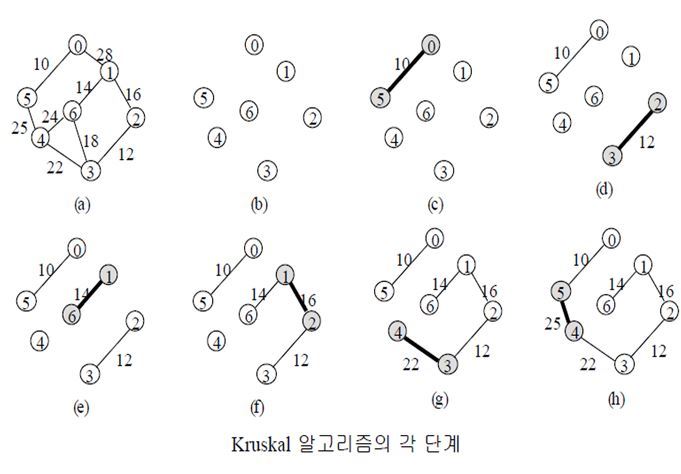
크루스칼 알고리즘은 간선의 개수가 E개일 때, $O(ElogE)$의 시간 복잡도를 가진다. 왜냐하면 크루스칼 알고리즘에서 시간이 가장 오래 걸리는 부분이 간선을 정렬하는 작업이며, E개의 데이터를 정렬했을 때의 시간 복잡도는 $O(ElogE)$이기 때문이다.

백준 1197번 문제

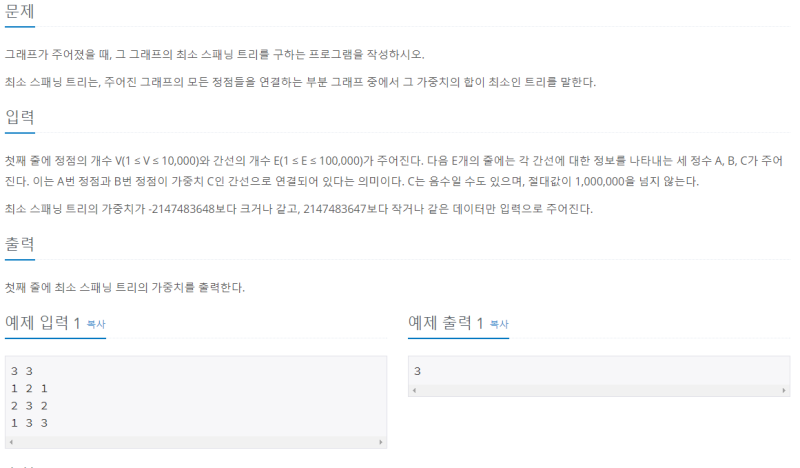
크루스칼 알고리즘을 사용하여 최소 신장 트리를 구할 수 있다.

import sys
input = lambda : sys.stdin.readline().rstrip()

V, E = map(int, input().split())
parent = list(range(V + 1)) # 부모를 자기 자신으로 초기화

#특정 원소가 속한 집합 찾기
def find(x):
    #루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀호출
    if x != parent[x]:
        parent[x] = find(parent[x])
    return parent[x]

# 두 원소가 속한 집합을 합치기
def union(a, b):
    a = find(a)
    b = find(b)
    if a > b:
        parent[b] = a
    else:
        parent[a] = b

edge = []
for _ in range(E):
    a, b, c = map(int, input().split())
    edge.append((a, b, c))
edge.sort(key=lambda x : x[2]) # 가중치 순으로 정렬

ans = 0
for a, b, c in edge:
    if find(a) != find(b): # 사이클이 발생하지 않는 경우
        union(a, b)
        ans += c
print(ans)