플로이드-워셜 알고리즘 - 백준 11404 (22.6.19)

플로이드 워셜 알고리즘이란

플로이드-워셜(Floyd-Warshall) 알고리즘은 한 번 실행하여 모든 노드 간 최단 경로를 구할 수 있는 알고리즘이다.

다익스트라 알고리즘과 비교를 하면서 설명하자면, 다익스트라 알고리즘은 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택한다.

플로이드 알고리즘 또한 단계마다 '거쳐 가는 노드'를 기준으로 알고리즘을 수행한다. 하지만 매번 최단 거리를 가지는 노드를 찾을 필요가 없다.


노드의 개수가 N개일 때 알고리즘상으로 N번의 단계를 수행하며, 단계마다 $O(N^2)$의 연산을 통해 '현재 노드를 거쳐가는' 모든 경로를 고려한다. 따라서 플로이드 워셜 알고리즘의 총시간 복잡도는 $O(N^3)$이다.

다익스트라 알고리즘에서는 출발 노드가 1개이므로 1차원 리스트를 이용한 반면, 모든 노드에 대하여 다른 모든 노드로 가는 최단 거리 정보를 담아야 하기 때문에 2차원 리스트를 사용해야 한다.


각 단계에서는 해당 노드를 거쳐 가는 경우를 고려한다. 최단 기록 테이블의 A->B비용이 해당 노드인 K노드를 거쳐 A->K->B 보다 크면, 비용을 갱신하는 것이다.

다이나믹 프로그래밍이라고 볼 수 있다. $D_{ij}$가 $i$에서 $j$까지의 최소거리라고 할 때 K번의 단계에 대한 점화식은 다음과 같다.

$D_{ab} = min(D_{ab}, D_{ak} + D_{kb}$)

백준 11404번 문제

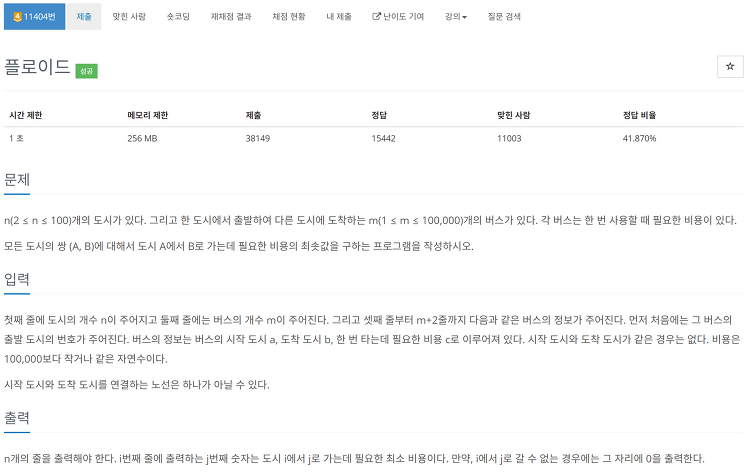
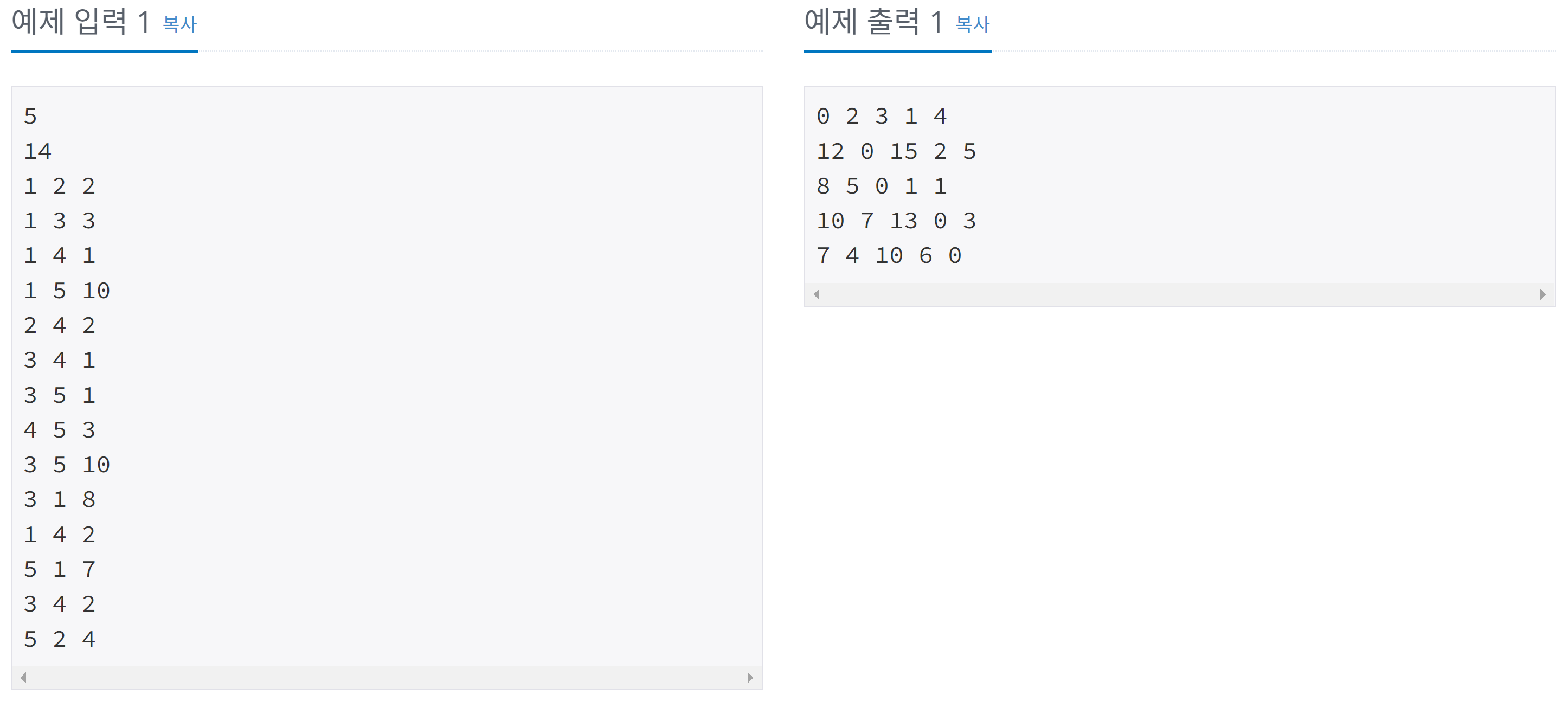
전형적인 플로이드 워셜 알고리즘 문제이다.

import sys
input = lambda : sys.stdin.readline().rstrip()
INF = 987654321

N = int(input())
M = int(input())
graph =[[INF] * (N + 1) for _ in range(N + 1)] # 무한으로 초기화
for _ in range(M):
    a, b, c = map(int, input().split())
    graph[a][b] = min(graph[a][b], c)

for k in range(1, N + 1):
    for a in range(1, N + 1):
        for b in range(1, N + 1): # 최단 기록 테이블의 A->B비용과 A->K->B 비용 중 작은 것을 기록 
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

for a in range(N + 1):
    for b in range(N + 1):
        if a == b or graph[a][b] == INF:
            graph[a][b] = 0

for i in range(1, N + 1):
    print(*graph[i][1:])