[자료구조] 그래프(Graph)

그래프(Graph) 란?

그래프는 vertex(정점)와 edge(정점과 정점을 연결하는 간선)로 구성된 한정된 자료구조를 의미한다.

그래프 종류

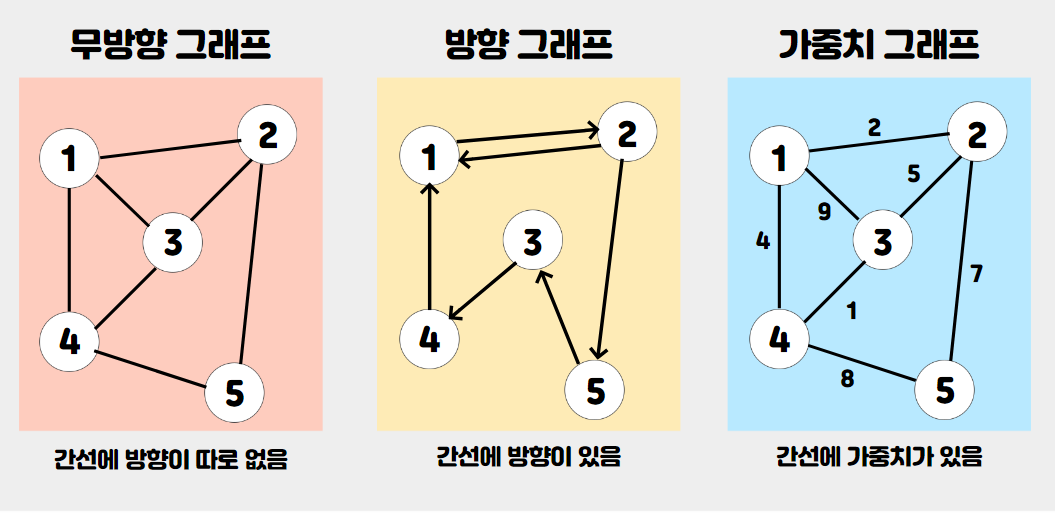
• 무방향 그래프 (간선에 방향이 따로 없음)
• 방향 그래프 (간선에 방향이 있음)
• 가중치 그래프 (간선에 가중치가 있음)

https://born2bedeveloper.tistory.com/42

그래프 구현

행렬로 구현하기

• 무방향 그래프
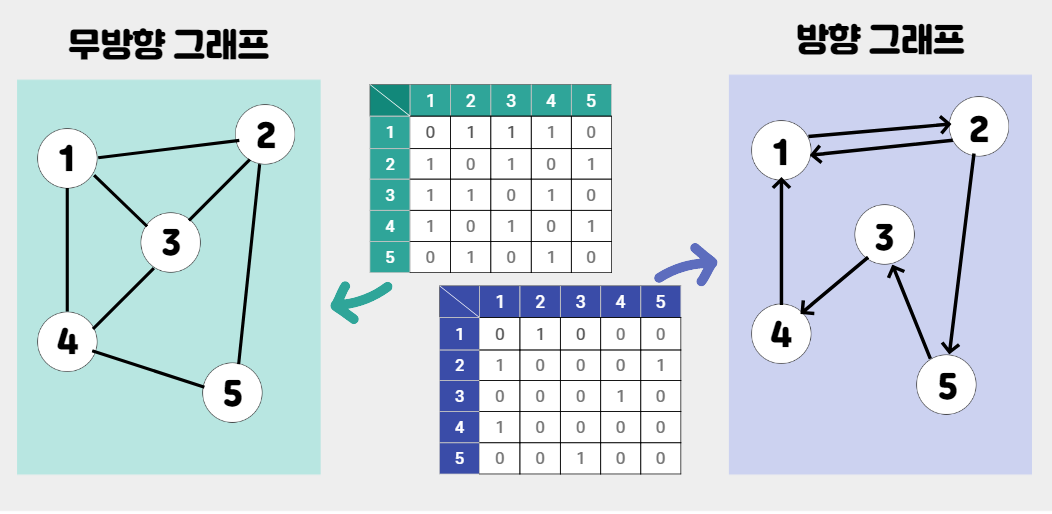
  정점 a와 정점 b를 잇는 간선이 있을 경우, 행렬(a,b)에 1을 표기한다.
  만약 가중치가 있는 그래프라면 1 대신 가중치를 넣을 수 있다.
  기본적으로 무방향 그래프의 경우는 (a,b) (b,a)에 모두 간선 값을 넣지만, 방향 그래프같은 경우는 위의 표와 같이 방향에 맞는 간선만 표기한다.

https://born2bedeveloper.tistory.com/42

• 무방향 그래프 코드 구현

public class Main {
 
    public static void print(int[][] graph) {
        for (int i = 1; i < graph.length; i++) {
            for (int j = 1; j < graph.length; j++)
                System.out.print(graph[i][j]+ " ");
            System.out.println();
        }
    }
 
    public static void putEdge(int[][] graph, int x, int y) {
        graph[x][y] = 1;
        graph[y][x] = 1;
    }
 
    public static void main(String[] args) {
        int n = 5; //그래프 정점의 개수
        int[][] graph = new int[n+1][n+1]; //index를 1부터 맞추기 위해 n+1
 
        putEdge(graph, 1, 2);
        putEdge(graph, 1, 3);
        putEdge(graph, 1, 4);
        putEdge(graph, 2, 3);
        putEdge(graph, 2, 5);
        putEdge(graph, 3, 4);
        putEdge(graph, 4, 5);
 
        print(graph);
 
    }
}

인접 리스트로 구현하기

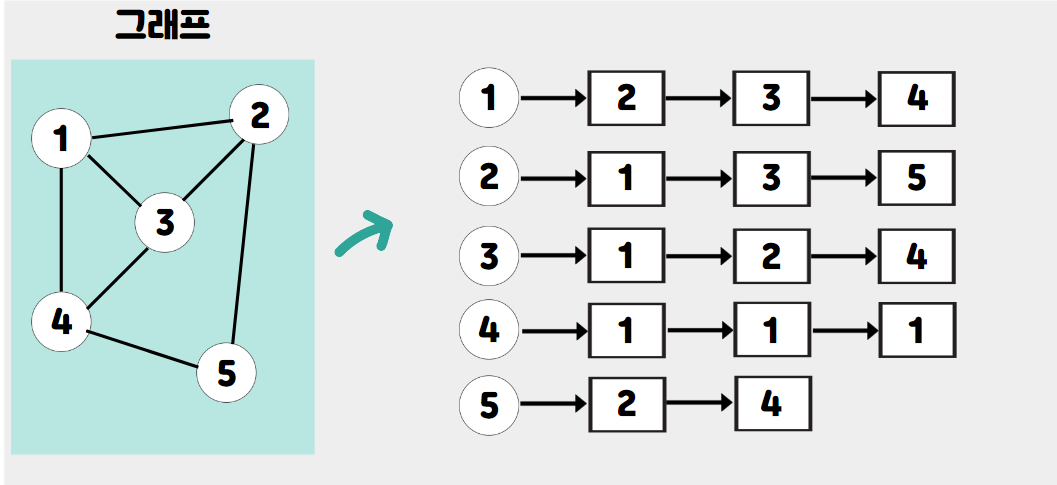
해당 노드와 연결되어있는 노드들을 리스트로 쭉 붙이는 방식이다.

https://born2bedeveloper.tistory.com/42

• ArrayList 사용하여 코드로 구현

public class Main {
 
    public static void print(ArrayList<ArrayList<Integer>> graph) {
        for (int i = 1; i < graph.size(); i++) {
            ArrayList<Integer> node = graph.get(i);
            System.out.print("node"+"["+i+"] : ");
            for (int j = 0; j < node.size(); j++)
                System.out.print(node.get(j)+ "->");
            System.out.println();
        }
    }
 
    public static void putEdge(ArrayList<ArrayList<Integer>> graph, int x, int y) {
        graph.get(x).add(y);
        graph.get(y).add(x);
    }
 
    public static void main(String[] args) {
        int n = 5; //그래프 정점의 개수
        ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
 
        for (int i = 0; i <= n; i++)
            graph.add(new ArrayList<>()); //각 노드 별 리스트를 만들어준다.
        putEdge(graph, 1, 2);
        putEdge(graph, 1, 3);
        putEdge(graph, 1, 4);
        putEdge(graph, 2, 3);
        putEdge(graph, 2, 5);
        putEdge(graph, 3, 4);
        putEdge(graph, 4, 5);
 
        print(graph);
 
    }
}

	인접 행렬	인접 리스트
시간 복잡도	O(N^2) 정점 N*N만큼 필요	O(N) N : 간선의 개수
두 정점의 연결 여부	graph[x][y] 의 값으로 한번에 확인	graph\ 의 원소에서 y가 나올때까지 탐색
인접 노드 파악 여부	N * N만큼 반복문을 돌아 확인	각 리스트에 담겨있는 원소를 확인

👉 간선이 많은 그래프의 경우, 인접 행렬을 통해 빠르게 연결 여부를 확인할 수 있음.
👉 반면 간선이 적은 그래프의 경우는, 인접 리스트를 통해 인접 노드를 빠르게 확인할 수 있음.

Reference

• 어? 되네? 어? 안되네? (tistory)