[자료구조] 우선순위 큐(Priority Queue)와 힙(Heap)

HONGKYUMIN (ANTHONY)·2022년 8월 14일

우선순위 큐(Priority Queue)자료구조 힙(Heap)

❗ 자바에서는 현재 우선순위큐(Priority Queue)를 이용하여 최대 힙, 최소 힙을 간단하게 사용할 수 있도록 제공해주고 있다.

우선순위 큐(Priority Queue)란?

우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조이다.
우선순위 큐는 데이터를 우선순위에 따라 처리하고 싶을 때 사용한다.
ex)물건 데이터를 자료구조에 넣었다가 가치가 높은 물건부터 꺼내서 확인해야 하는 경우
우선순위 큐를 구현하는 방법
1. 단순히 리스트를 이용하여 구현가능
2. 힙(heap)을 이용하여 구현 가능
단순히 N개의 데이터를 힙에 넣었다가 모두 꺼내는 작업은 정렬과 동일하다.(힙 정렬 O(NlogN))

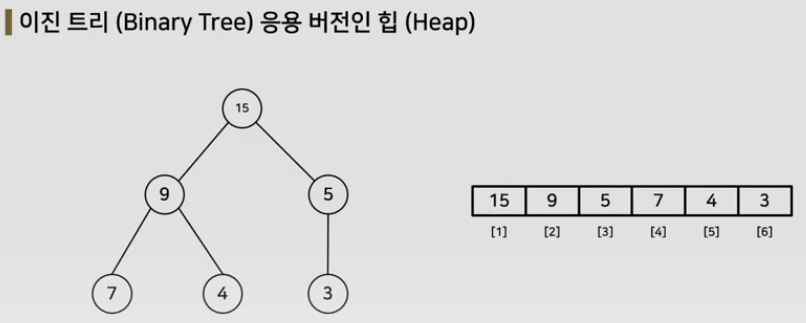
힙(Heap)이란?

완전 이진 트리 자료구조의 일종이다.
힙에서는 항상 루트 노드(root node)를 제거한다.
최소 힙(min heap)
- 루트 노드가 가장 작은 값을 가진다.
- 따라서 값이 작은 데이터가 우선적으로 제거된다.
최대 힙(max heap)
- 루트 노드가 가장 큰 값을 가진다.
- 따라서 값이 큰 데이터가 우선적으로 제거된다.
일반적으로 그룹을 정렬(Sort)하거나 입력된 데이터 안에서 최소/최대 값을 찾을 때 사용한다.
데이터 삽입과 삭제가 빠르며, 각각의 수행시간 : O(log N)

힙의 1차원 배열
❗ 배열로 구현했을 때, 오름차순 내림차순으로 정렬되는 것은 아니다.

힙의 구현

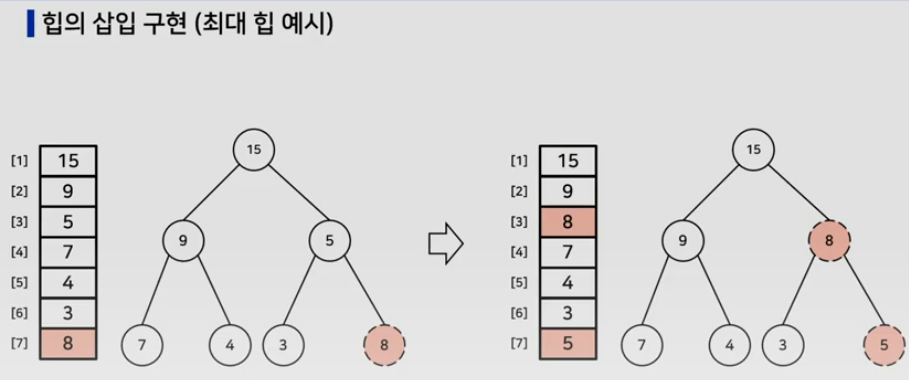
힙의 삽입 연산

트리의 가장 마지막 위치에 노드를 삽입
추가된 노드와 그 부모 노드가 힙 조건을 만족하는지 확인 -> 힙 조건은 최대힙/최소힙에 따라 다르다
만족하지 않는다면 부모와 자식의 키 값을 바꾼다
조건에 만족하거나 추가된 노드가 루트에 도달할 때까지 2~3번을 반복한다

완전 이진 트리의 리프 노드부터 루트 노드까지 연산을 한다.

노드가 N개일 때 수행시간 O(log N)
힙의 삽입 연산

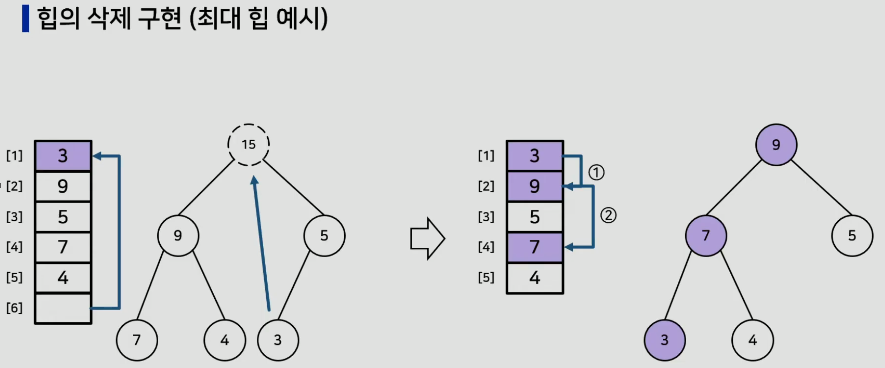
힙의 삭제 연산

힙의 삭제연산은 항상 루트 노드를 삭제
트리의 가장 마지막 노드를 루트 자리로 삽입
바꾼 위치의 노드가 힙 조건을 만족하는지 확인 -> 힙조건은 최대힙/최소힙에 따라 다르다
만족하지 않는다면 왼쪽 자식과 오른쪽 자식 중 적합한 노드와 키 값을 바꿈
조건을 만족하거나 리프 노드에 도달할 때까지 3~4번을 반복

완전 이진 트리의 리프 노드부터 루트 노드까지 연산을 한다.

노드가 N개일 때 수행시간 O(log N)
힙의 삭제 연산

배열에서의 힙 요소 위치 찾기

idx : 해당 요소의 배열 순번

idx-1 / 2 : 부모 위치
2 * idx + 1 : 왼쪽 자식 위치
2 * idx + 2 : 오른쪽 자식 위치

힙(Heap)의 용도

위상정렬
최대값 뽑아내기 등

코드 구현

//최소 힙
PriorityQueue<Integer> minHeap = new PriorityQueue<>();

//최대 힙
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());

메소드는 Queue와 동일.