트리
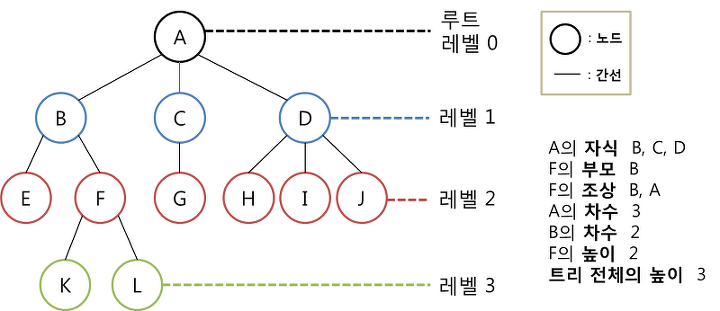
용어
- 루트 : 트리의 가장 윗부분에 위치한 노드이다.
- 리프 : 트리의 가장 아랫부분에 위치한 노드이다. 물리적으로 가장 아래부분에 위치한다는 의미가 아닌, 더 이상 뻗어나갈 수 없는 마지막에 노드가 위치한다는 말이다.
- 안쪽 노드 : 루트를 포함하여 리프를 제외한 노드를 말한다.
- 자식 : 어떤 노드로부터 가지로 연결된 아랫쪽 노드를 말한다.
- 부모 : 어떤 노드에서 가지로 연결된 위쪽 노드를 말한다
- 형제 : 같은 부모를 가지는 노드를 말한다.
- 조상 : 어떤 노드에서 가지로 연결된 위쪽 노드 모두를 말한다.
- 자손 : 어떤 노드에서 가지로 연결된 아래쪽 노드 모두를 말한다.
- 레벨 : 루트로부터 얼마나 떨어져 있는지에 대한 값이다. 루트의 레벨은 0이고 가지가 하나씩 아래로 뻗어나갈 때마다 레벨이 1씩 증가한다.
- 차수 : 노드가 갖는 자식의 수를 말한다. 모든 노드의 차수가 n 이하인 트리를 n진 트리라고 한다.
- 높이 : 루트로부터 가장 멀리 떨어진 리프까지의 거리를 말한다.
- 서브 트리 : 트리 안에서 다시 어떤 노드를 루트로 정하고 그 자손으로 이루어진 트리를 서브 트리라고 한다.
- 널 트리 : 노드, 가지가 없는 트리를 말한다.
- 순서 트리와 무순서 트리 : 형제노드의 순서를 따지면 순서트리, 따지지 않으면 무순서 트리라고 한다.
순서 트리의 탐색
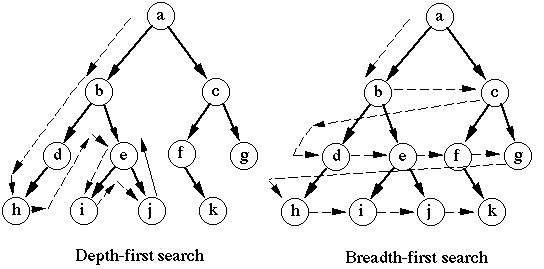
너비 우선 탐색
- 낮은 레벨에서 시작해 왼쪽에서 오른쪽 방향으로 검색하고 다음 레벨로 내려간다.
깊이 우선 탐색
- 리프까지 내려가면서 검색하는 것을 우선순위로 하는 탐색방법이다.
- 세가지 방법이 있다.
- 전위 순회(preorder)
- 노드 방문 -> 왼쪽 자식 -> 오른쪽 자식
- a - b - d - h - e - i - j - c - f - k - g
- 중위 순회(inorder)
- 왼쪽 자식 -> 노드 방문 -> 오른쪽 자식
- h - d - b - i - e - j - a - k - f - c - g
- 후위 순회(postorder)
- 왼쪽 자식 -> 오른족 자식 -> 노드 방문
- h - d - i - j - e - b - k - f - g - c - a
이진 트리
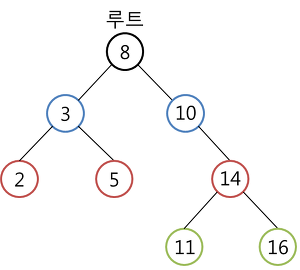
- 노드가 왼쪽 자식과 오른쪽 자식을 갖는 트리를 이진트리라고 한다.
완전 이진 트리
- 마지막 레벨을 제외한 레벨은 노드가 가득 채워져 있다.
- 마지막 레벨은 왼쪽부터 오른쪽 방향으로 노드가 채워져 있다.
이진 검색 트리
- 어떤 노드 N을 기준으로 왼쪽 서브 트리 노드의 모든 키 값은 노드 N의 키 값보다 작다.
- 오른쪽 서브 트리 노드의 키 값은 노드 N의 키 값보다 크다.
- 같은 키 값을 갖는 노드는 없다.

