정렬 알고리즘 sorting algorithm (Python)

yuseon Lim·2021년 7월 6일

algorithm python

algorithm

목록 보기

1/4

📌 버블 정렬 (Bubble sort)

두 인접한 원소를 검사하여 정렬하는 방법
시간복잡도가 $O(N^{2})$ 으로 좋지 않음
그러나 구현이 단순

예시

다음 배열을 버블 정렬로 오름차순 정렬 해 보겠다
처음 3, 5는 이미 오름차순으로 정렬 되어 있다
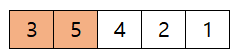
다음 5, 4는 swap 한다
다음 5, 2는 swap 한다
다음 5, 1도 swap 한다

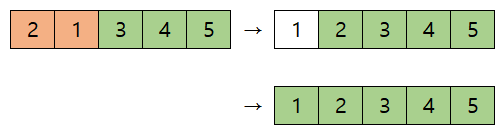
여기까지 하면, 가장 큰 5는 오름차순에 맞게 맨 뒤로 이동했다. 다음 차례에는 5를 제외한 나머지 원소들에 대해 정렬하면 된다. 이 과정을 계속 반복한다.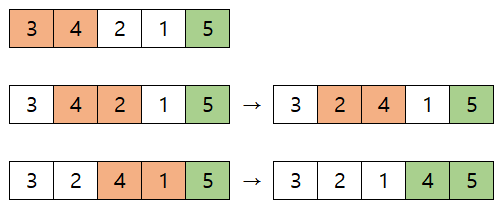

소스코드

# 재귀
def bubble_sort_recur(arr: list, last: int):
    if last > 0:
        for i in range(0, last):
            if arr[i] > arr[i + 1]:
                arr[i], arr[i + 1] = arr[i + 1], arr[i]
        bubble_sort_recur(arr, last - 1)

# 반복
def bubble_sort_iter(arr: list):
    last = len(arr) - 1
    while (last > 0):
        for i in range(0, last):
            if arr[i] > arr[i + 1]:
                arr[i], arr[i + 1] = arr[i + 1], arr[i]
        last -= 1

            
arr = [3, 5, 4, 2, 1]
print(arr) # [3, 5, 4, 2, 1]
bubble_sort_recur(arr, len(arr) - 1)
print(arr) # [1, 2, 3, 4, 5]

arr = [3, 5, 4, 2, 1]
print(arr) # [3, 5, 4, 2, 1]
bubble_sort_iter(arr)
print(arr) # [1, 2, 3, 4, 5]

📌 선택 정렬 (Selection sort)

제자리 정렬 알고리즘의 하나
다음과 같은 순서로 이루어짐
1. 주어진 리스트 중 최솟값 찾는다.
1. 그 값을 맨 앞에 위치한 값과 swap
2. 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 swap
시간복잡도가 $O(N^{2})$ 이다.

예시

3,5,4,2,1 을 정렬하는 과정은 다음과 같다.
'

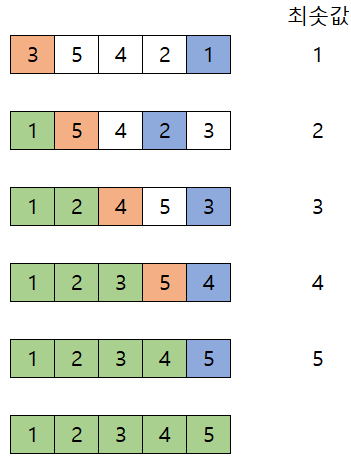소스코드

# 재귀
def selection_sort_recur(arr: list, start: int):
    if start < len(arr) - 1:
        min_index = start
        # 이 과정은 리스트를 slice 하여
        # 파이썬의 min()메소드를 사용해도 됨
        for i in range(start + 1, len(arr)):
            if arr[min_index] > arr[i]:
                min_index = i
        arr[start], arr[min_index] = arr[min_index], arr[start]
        selection_sort_recur(arr, start + 1)

# 반복
def selection_sort_iter(arr: list, start: int):
    while start < len(arr) - 1:
        min_index = start
        for i in range(start + 1, len(arr)):
            if arr[min_index] > arr[i]:
                min_index = i
        arr[start], arr[min_index] = arr[min_index], arr[start]
        start += 1


arr = [3, 5, 4, 2, 1]
print(arr) # [3, 5, 4, 2, 1]
selection_sort_recur(arr, 0)
print(arr) # [1, 2, 3, 4, 5]

arr = [3, 5, 4, 2, 1]
print(arr) # [3, 5, 4, 2, 1]
selection_sort_iter(arr, 0)
print(arr) # [1, 2, 3, 4, 5]

📌 삽입 정렬 (Insertion sort)

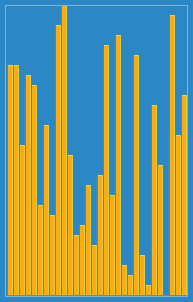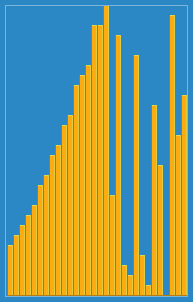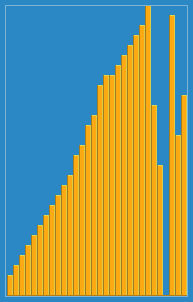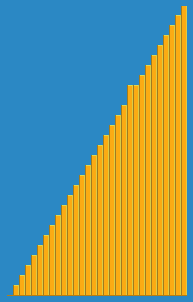
자료 배열의 모든 요소를 앞에서부터 차례대로
이미 정렬된 배열 부분과 비교
자신의 위치를 찾아 삽입
시간복잡도는 $O(N^{2})$

예시

3, 5, 4, 2, 1 을 정렬하는 예제이다.

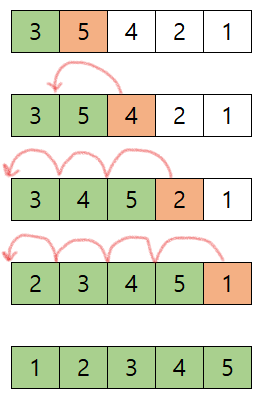
소스코드

# 재귀
def insertion_sort_recur(arr: list, cur: int):
    if cur < len(arr):
        for i in range(cur, -1, -1):
            if arr[i] > arr[cur]:
                arr[i], arr[cur] = arr[cur], arr[i]
            else:
                insertion_sort_recur(arr, cur + 1)
    else:
        return

# 반복
def insertion_sort_iter(arr: list):
    for cur in range(1, len(arr)):
        for j in range(cur, 0, -1):
            if arr[j] > arr[cur]:
                arr[cur], arr[j] = arr[j] , arr[cur]
        
        
arr = [3, 5, 4, 2, 1]
print(arr) # [3, 5, 4, 2, 1]
insertion_sort_recur(arr, 1)
print(arr) # [1, 2, 3, 4, 5]

arr = [3, 5, 4, 2, 1]
print(arr) # [3, 5, 4, 2, 1]
insertion_sort_iter(arr)
print(arr) # [1, 2, 3, 4, 5]

📌 합병 정렬 (Merge sort)

비교 기반 알고리즘
안정 정렬에 속하며 분할 정복 알고리즘의 하나
그 유명한 폰 노이만이 개발했다고 한다
퀵 정렬과 유사하나, 최악의 경우에도 시간복잡도가 $O(NlogN)$ 이 보장된다.
- divde 할 수록 반씩 줄어드니 $logN$ 이고,
- 이것을 정렬을 하기 위해서 결국 n번 반복하니 $O(NlogN)$ 이다.
그러나 정렬을 위한 별도의 저장공간이 필요해 공간적으로는 퀵 소트보다 좋지 않다.

예시

3, 9, 4, 7, 5, 0, 1, 6, 8, 2 을 정렬하는 예시이다.

divide 한다 이때 가장 작은 단위로 쪼개면 하나씩 나눠지지만 그것은 정렬된 상태이기때문에 생략 생략된 단계에서 두개씩은 모두 정렬된 상태로 끝난다. 그 결과가 아래 그림
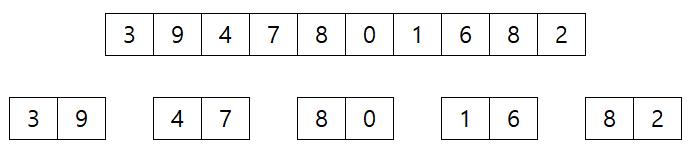
정렬 한다
Merge 한다. 3,9 / 4,7 을 merge 하는 과정은 이렇다.
(start는 0, mid는 1 end는 3 일 때)3, 4중 3이 작으므로 arr의 index 0에 3 복사하고, part1 1 증가, index 1 증가, 1
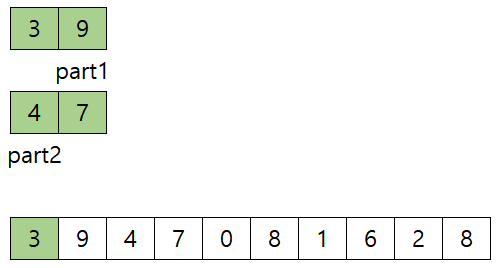
9와 4중 4가 작으므로 arr의 index 1에 4 복사하고, part2 1 증가, index 1 증가, 2![]
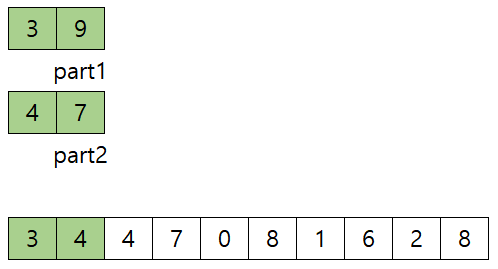
9와 7중 7이 작으므로 arr의 index 2에 7을 복사하고, part2 1 증가, index 1 증가, 3
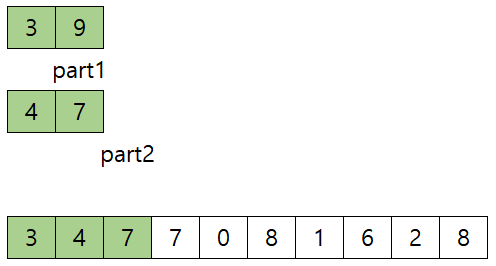
이제 part1이 1, part2 가 4로, end값인 3보다 크기 때문에
아래 코드를 수행하게 된다.

for i in range(0, mid - part1 + 1):
        arr[index + i] = tmp[part1 + i]

그럼 이렇게 된다
이 과정을 계속 반복한다.

소스코드

def merge_sort(arr: list[int], tmp: list[int], start: int, end: int) :
    if start < end:
        mid: int = (start + end) // 2
        merge_sort(arr, tmp, start, mid) # 계속해서 쪼갬
        merge_sort(arr, tmp, mid + 1, end) # 쪼갬
        merge(arr, tmp, start, mid, end) # 합병

def merge(arr: list[int], tmp: list[int], start: int, mid: int, end: int):
    for i in range(start, end + 1):
        tmp[i] = arr[i] # 임시 배열에 복사

    part1 = start
    part2 = mid + 1
    index = start

    while part1 <= mid and part2 <= end:
        if tmp[part1] <= tmp[part2]:
            arr[index] = tmp[part1]
            part1 += 1
        else:
            arr[index] = tmp[part2]
            part2 += 1
        index += 1
    
    # 뒤쪽 배열에 데이터 남음
    for i in range(0, mid - part1 + 1):
        arr[index + i] = tmp[part1 + i]


arr = [3, 9, 4, 7, 5, 0, 1, 6, 8, 2]
tmp = [int] * len(arr)
print(arr) # [3, 9, 4, 7, 5, 0, 1, 6, 8, 2]
merge_sort(arr, tmp, 0, len(arr) - 1)
print(arr) # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

📌 퀵 정렬 (Quick sort)

비교 정렬에 속한다.
퀵 정렬은 최악의 경우에 $O(N^{2})$ 가 되고 평균적으로는 $O(NlogN)$ 이다.
- 최악의 경우는 pivot값이 계속 양 끝이 되는 경우 이다.

예시

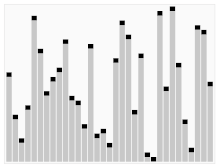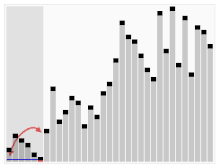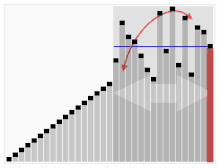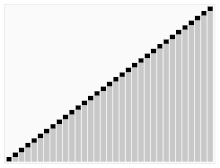
아래 그림과 같은 배열을 정렬한다. pivot값은보통 좌측 끝, 우측 끝, 가운데로 정하는데, 이 예시에서는 가운뎃값을 pivot으로 설정했다.
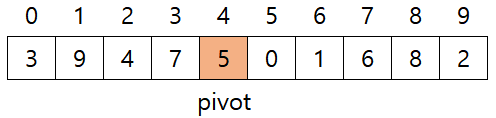
3은 5보다 작으니 무시, 9는 5보다 크니 멈춘다. 2는 5보다 작으니 멈춘다.
swap
start, end 포인트를 각 각 하나씩 증가, 감소 시킨 뒤 다시 똑같은것을 반복한다. 4가 5보다 작으니 무시, 7이 5보다 크니 멈춘다. 8, 6이 5보다 크니 무시, 1이 5보다 작으니 멈춘다. 그리고 swap 한다.
아직 start와 end가 만나지 않았다. start를 증가, end를 감소시킨다. 이제 start가 pivot의 자리까지 왔다. pivot과 같으니 멈춘다. 0은 5보다 작으니 멈춘다. swap 한다.
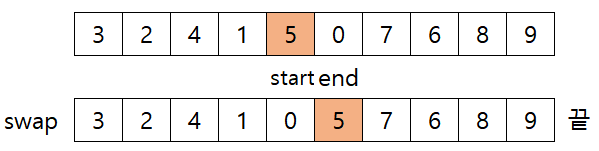
이 과정을 pivot전과, pivot을 포함한 후 배열을 재귀 호출 한다.
계속 반복하면 정렬이 된다.

소스코드

def quick_sort(arr: list, start: int, end: int):
    # start와 end사이에서 파티션을 나누고
    # 나눈 파티션의 오른쪽 방 첫 번째 값을 받아옴
    part2 = partition(arr, start, end)

    # start와 part2가 한개 이상 차이 날 때만.
    # 한개 이상 차이가 나지 않는다? = 정렬 할 필요가 없음
    if 1 < part2 - start: 
        # 왼쪽 파티션.
        # 끝점이 오른쪽 파티션의 시작점 바로 왼쪽
        quick_sort(arr, start, part2 - 1)
    # 오른쪽 파티션의 배열방이 한개 이상일 때만 호출
    # 오른쪽 파티션의 시작점이 마지막 배열방 보다 작은 경우에만
    # 오른쪽 파티션을 정렬
    if part2 < end:
        quick_sort(arr, part2, end)

def partition(arr: list, start: int, end: int):
    pivot = arr[(start + end) // 2] # pivot을 중간에있는값으로
    while start <= end:
        # 왼쪽부터 차례대로 검사하는데,
        # arr[start] 가 pivot보다 작으면 무시하고 넘어감
        # 크거나 같으면 멈춤
        while arr[start] < pivot: start += 1
        # 오른쪽은, arr[end] 값이 pivot보다 크면 무시하고 넘어감
        # 작거나 같으면 멈춤
        while arr[end] > pivot: end -= 1
        # 시작점과 끝점이 만나지는 않았는지 검사
        # 안만났으면 swap
        if start <= end:
            arr[start], arr[end] = arr[end], arr[start]
            start += 1
            end -= 1
        # 이 과정을 start와 end가 만나서 지나칠때까지 반복
    return start # 새로 나눌 오른쪽 파티션의 첫번째 배열방 인덱스 반환


arr = [3, 9, 4, 7, 5, 0, 1, 6, 8, 2]
print(arr)
quick_sort(arr, 0, len(arr) - 1)
print(arr)

📌 힙 정렬 (Heap sort)

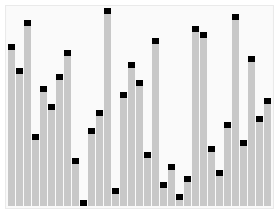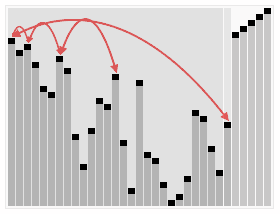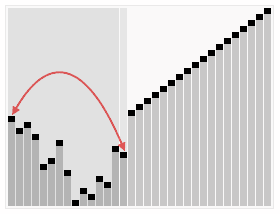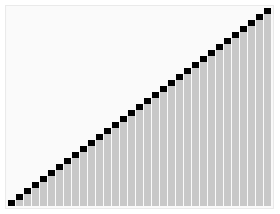
최대 힙 트리나 최소 힙 트리를 구성해 정렬
내림차순 -> 최대 힙
오름차순 -> 최소 힙
순서는 이렇다.
1. n개의 노드에 대한 완전 이진 트리를 구성한다. 이때 루트 노드부터 부모 노드, 왼쪽 자식 오른쪽 자식 노드 순으로 구성한다.
  🐋 완전 이진 트리란?
  - 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있다.
  - 마지막 레벨의 모든 노드는 가능한 가장 왼쪽에 있다.
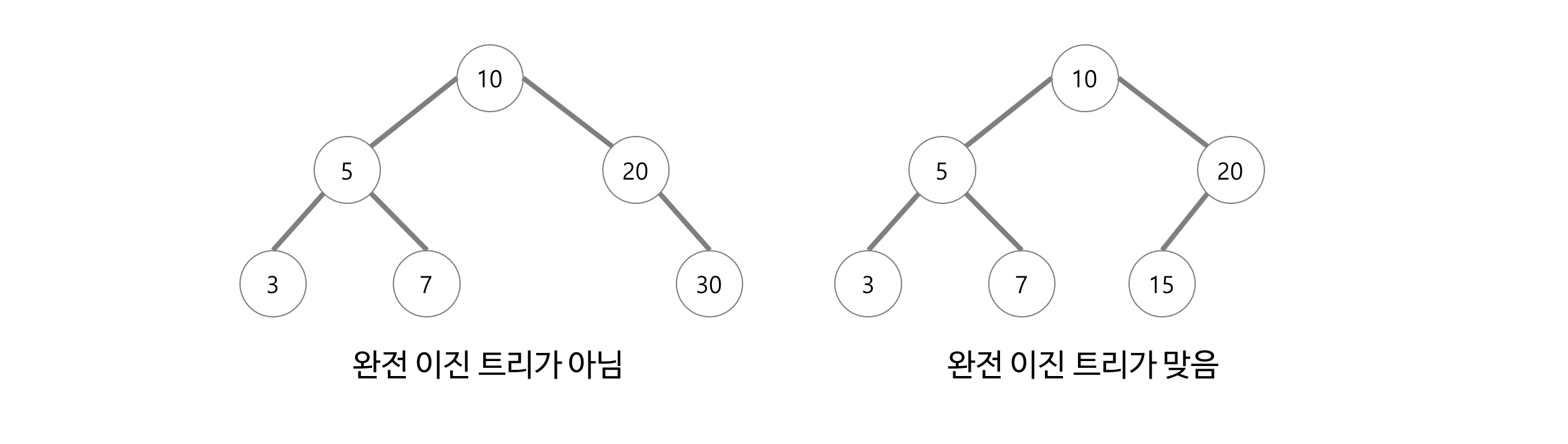
2. 최대 힙을 구성한다. (최대 힙이란 부모노드가 자식 노드보다 큰 트리) 단말 노드를 자식노드로 가진 부모노드로부터 구성하며 아래부터 루트까지 올라오며 순차적으로 만들어 갈 수 있다.
3. 가장 큰 수(루트에 위치)를 가장 작은 수와 교환한다.
4. 2와 3을 반복한다.
이진 트리의 깊이만큼 이루어 지므로 최대 힙을 구성하는데에 $O(logn)$ 의 수행시간이 걸리고
구성된 최대 힙으로 힙 정렬을 수행하는데 n개의 데이터 삭제 및 재구성 시간이 걸리므로 일반적으로 힙 정렬은 $O(NlogN)$ 의 시간복잡도를 가진다.

소스코드 (아직 미 구현)

참고> Python의 heapq 모듈을 이용한 힙 정렬

✨ 성능 비교

Sorting	Average	Worst	Memory	Stable
버블 정렬	$O(N^{2})$	$O(N^{2})$	$O(1)$	O
선택 정렬	$O(N^{2})$	$O(N^{2})$	$O(1)$	X
삽입 정렬	$O(N^{2})$	$O(N^{2})$	$O(1)$	O
합병 정렬	$O(NlogN)$	$O(NlogN)$	$O(N)$	O
퀵 정렬	$O(NlogN)$	$O(N^{2})$	$O(1)$	X
힙 정렬	$O(NlogN)$	$O(NlogN)$	$O(1)$	X

👀 Stable 하다?

정렬 후에도 같은 키들의 상대적인 순서가 정렬 이전과 동일하게 유지되는 정렬 방법.

🔎 백준 문제 풀이

문제	풀이링크
백준 11652 - 카드	🔗
백준 10989 - 수 정렬하기3	🔗
백준 11728 - 배열 합치기	🔗
백준 5052 - 전화번호 목록	🔗
백준 1202 - 보석 도둑	🔗

참고자료

yuseon Lim

🔥https://devyuseon.github.io/ 로 이사중 입니다!!!!!🔥

다음 포스트

정렬 알고리즘 sorting algorithm (Python)

algorithm

📌 버블 정렬 (Bubble sort)

예시

소스코드

📌 선택 정렬 (Selection sort)

예시

소스코드

📌 삽입 정렬 (Insertion sort)

예시

소스코드

📌 합병 정렬 (Merge sort)

예시

소스코드

📌 퀵 정렬 (Quick sort)

예시

소스코드

📌 힙 정렬 (Heap sort)

소스코드 (아직 미 구현)

참고> Python의 heapq 모듈을 이용한 힙 정렬

✨ 성능 비교

👀 Stable 하다?

🔎 백준 문제 풀이

참고자료

그리디 알고리즘 Greedy Algorithm (Python)

0개의 댓글