타원 곡선 공개키 암호 (ECC, Elliptic Curve Cryptography)
본 글은 한기대 박승철 교수님의 타원 곡선 암호 강의를 듣고 정리한 내용입니다.
현재까지 공개키 암호는 주로 RSA나 DH를 많이 사용해왔다. 최근에 들어서는 ECC(타원곡선 암호)를 많이 사용한다. ECC는 디지털 서명, 키 교환을 위한 공개키 암호로 주로 사용된다.
1. ECC 개요
타원 곡선 이산 대수 문제(ECDLP, Elliptic Curve Discrete Logarithm Problem)
- 타원 곡선 상의 알려진 점(P)을 더하여 새로운 점을 계산하는 회수를 나타내는 값(k)을 개인키로 하고,
- P를 k번 더해 생성되는 새로운 점에 해당하는 값(kP)을 공개키로 정의할 때, 공개키(kP)로부터 개인키(k)를 계산하는 문제
- 현재까지 빠른 계산을 도울 수 있는 방법이 거의 알려지지 않음
- 비밀로 유지되는 개인키를 알아내기 위해서는 오로지 전사 공격(brute force attack, 일일이 대입)에 의존해야 함
- 일부 빠른 계산 기법들의 도움을 받을 수 있는 소인수 분해나 지수 함수 이산 대수 연산(RSA에 활용)에 비해 같은 크기의 키를 사용할 때 훨씬 많은 수의 연산 수행 필요
보안 강도
| RSA | ECC |
|---|---|
| 1024 | 160 |
| 2048 | 224 |
| 3072 | 256 |
| 7680 | 384 |
| 15368 | 512 |
(단위 : 비트)
ECC가 RSA보다 훨씬 효율적임
응용 분야
- 디지털 서명
- 1회용 대칭키(세션키) 생성을 위한
Diffie-Hellman알고리즘
2. 타원 곡선 (Elliptic Curve)
기본 방정식
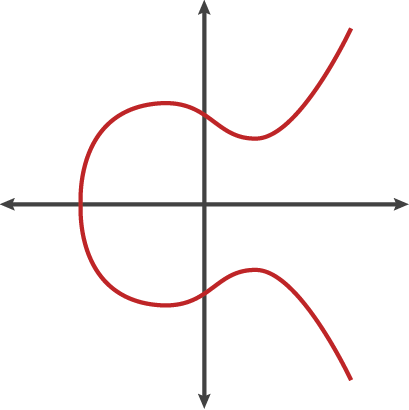
y^2 = x^3 + ax + b- y축에 2차, x축에 3차인 특수 방정식
비특이 타원 곡선 (nonsingular elliptic curve)
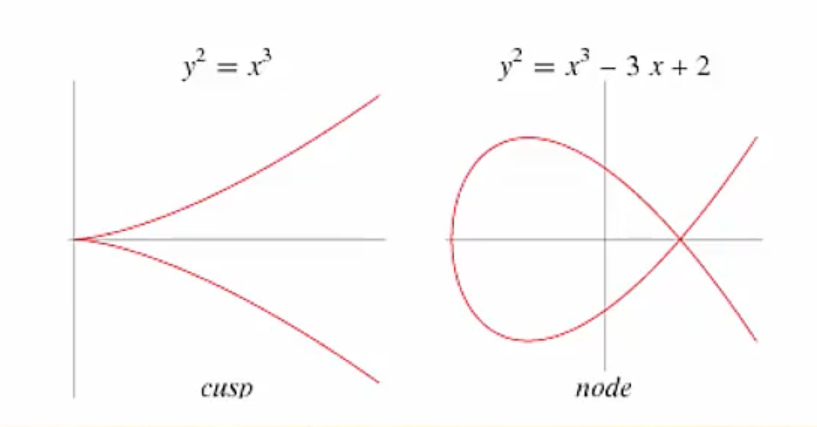
4a^3 + 27b^2 ≠ 0- 첨점(sharp point), 교차점(intersection point)이 존재하지 않는 타원 곡선
비특이 타원 곡선의 특징
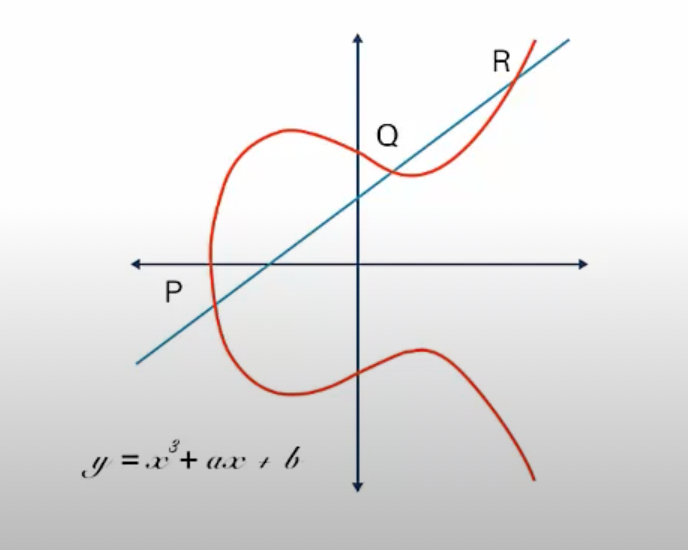
- x축 상에서 y의 값이 정확하게 대칭
- 두 점 P와 Q를 연결하는 직선은 반드시 다른 한 점(R)을 연결
- P와 Q가 동일할 때도 성립 : 접선(tangent)
타원 곡선 점(point)의 정의
- 점
P = (x, y), x는 x축의 값, y는 y축의 값 - 점
0 = (x, 0), y축의 값이 0인 점 - 점
-P = (x, -y), P의 x축 상의 대칭점(비특이 타원 곡선에서 반드시 존재)
3. 타원 곡선(Elliptic Curve) 점 덧셈 연산
정의
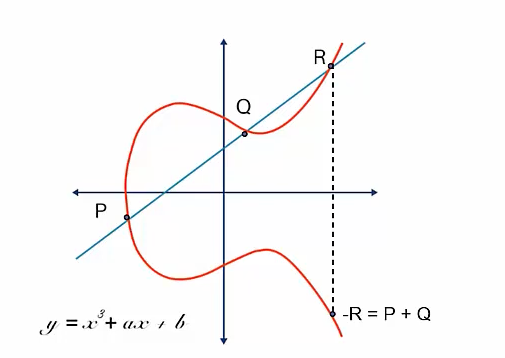
- 직선으로 연결되는 점 P, Q, R에 대해
P + Q + R = 0P + Q = -R(R의 대칭점)R + (-R) = R - R = 0
동일 점의 덧셈
P + P = 2P, P의 접선과 만나는 점의 대칭점

4. 타원 곡선(Elliptic Curve) 점 곱셈 연산
동일점 덧셈과 스칼라 곱셈(scalar multiplication) 연산
P + P + ... + P = kP(점 P의 k 스칼라 곱), k는 덧셈 횟수- 예)
8G = G + G + G + G + G + G + G + G
타원 곡선 점 곱셈
- 점의 스칼라 곱셈
5. 타원 곡선(Elliptic Curve) 점 연산 성질
결합법칙, 교환법칙, 분배법칙
3G = (G + G) + G = G + (G + G), 덧셈 결합법칙3G = 2G + G = G + 2G, 덧셈 교환법칙(2 + 2)G = 2G + 2G, 덧셈과 스칼라 곱셈 분배법칙6G = 3(2G) = 2(3G), 스칼라 곱셈 교환법칙24G = 2(2(4G)) = 4(2(3G)), 스칼라 곱셈 결합법칙
항등원, 역원
- 덧셈 항등원 : 0
- P의 덧셈 역원 : -P
- 곱셈 항등원 : 1
- 곱셈 역원 : P^-1
6. 타원 곡선(Elliptic Curve) 점 배가 연산
배가 연산(doubling operation)
2G = G + G, G doubling4G = (2 + 2)G = 2G + 2G, 2G doubling8G = (4 + 4) = 4G + 4G, 4G doubling- (2^n)G 덧셈 횟수 =
n(log(2)2^n)
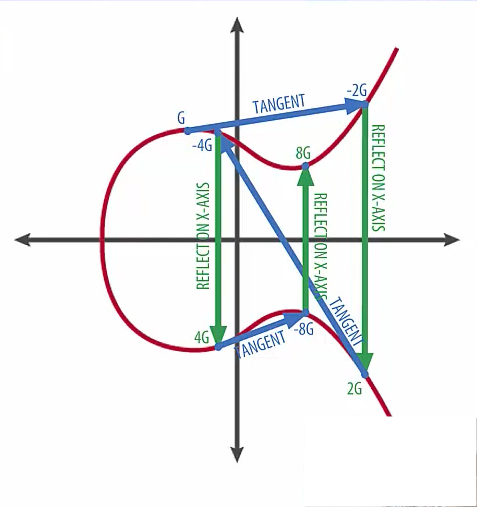
7. 타원 곡선(Elliptic Curve) 점 덧셈
빠른 덧셈 연산 : 배가와 덧셈(double-add) 알고리즘
- k(max) = n비트 이진수의 최대값 =
2^(n-1) + 2^(n-2) + ... + 2^0 - k(max)G = (2^(n-1) + 2^(n-1) + ... 2^0)G =
2^(n-1)G + 2^(n-2)G + ... + G - k(max)G 연산 횟수 = 배가 연산 (n-1)회 + 덧셈 연산 (n-1)회 =
2(n-1)회
k가 256비트 값인 경우
- kG의 최대 연산 횟수 = 255 + 255 = 510회
결론
- 비특이 타원 곡선에서 알려진 점 G에 대한 kG는 쉽게 계산 가능
8. 타원 곡선 이산 대수 연산
타원 곡선 이산 대수 문제
- K = xG에서 K와 G가 주어질 때 x를 구하는 문제
타원 곡선 이산 대수 문제의 해법
- 점 K로부터 점 G를 빼는 연산을 반복 수행
- 알려진 빠른 계산 방법이 없음
- 전통적인 지수 연산의 이산 대수 문제에 비해 훨씬 어려움
x가 n비트 값인 경우
- 최대 2^n회의 뺄셈 연산 수행
- x의 값이 커지면 매우 어려운 문제
9. 타원 곡선 암호
모듈로 p 타원 곡선 방정식
y^2 mod p = (x^3 + ax + b)mod p, p는 소수
모듈로 p 타원 곡선
- 동일한 덧셈과 스칼라 곱셈 연산에 대해 GF(2^n)
- 유한성, 폐쇄성, 결합성, 교환성, 분산성, 항등원, 역원
secp256k1 표준
- a = 0, b = 7, p = 2^256 - 2^32 - 2^9 - 2^7 - 2^6 - 2^4 - 1
개인키
- 정수 k
공개키
- kG
G
- (256비트의 값, 256비트의 값)
10. 타원 곡선 디지털 서명
k = 개인키, r = 비밀의 큰 수, kG = 공개키, m = 메시지
- hash(m, rG)kG + rG = (hash(m, rG)k + r)G
R = rG, s = hash(m, rG)k + r, K = kG
- hash(m,R)K + R = sG
메시지 m의 서명
- R과 s
서명 확인
- 수신 메시지 : m'
- Hash(m', R)K + R = sG가 성립하면 서명 확인 성공
서명 위조의 어려움
- R' = rG, 타원 곡선 이산 대수의 어려움으로 r 추론 불가
- s' = hash(m, rG)k + r, k와 r 추론 불가
서명 공개와 개인키 보호
- k = (s - r) / hash(m, R), r 추론 불가
11. 타원 곡선 Diffie-Hellman(ECDH)
사용자 A, 공개키를 B에게 전송
- 개인키 : kA
- 공개키 : K^(+)A = kAG
사용자 B, 공개키를 A에게 전송
- 개인키 : kB
- 공개키 : K^(+)B = kBG
사용자 A의 대칭키
- kA K^(+)B
사용자 B의 대칭키
- kB K^(+)A
증명
- kA·K^(+)B = kA·(kB·G) = kB·(kA·G) = kB·K^(+)A