Mastering Ethereum 4

개발새발·2021년 10월 24일

Mastering Ethereum

목록 보기

4/7

Chapter 4. 암호학

본 글은 『Mastering Ethereum』을 읽고 정리한 내용입니다.

이더리움의 기반 기술 중 하나는 컴퓨터 보안에 광범위하게 사용되는 수학의 한 분야인 암호학(cryptography)이다. 암호학은 그리스어로 비밀 작성을 의미하지만, 암호학 연구는 암호화(encryption)라고 하는 단순한 비밀 작성 이상의 것을 포함한다. 예를 들어 암호학은 그 비밀을 밝히지 않고 비밀의 지식을 증명하거나(예: 디지털 서명을 사용하여), 데이터의 진위성을 증명하는 데(예: 해시라고도 알려진 디지털 지문을 활용하여) 사용할 수 있다. 이런 유형의 암호화 증명은 이더리움 플랫폼(실제로 모든 블록체인 시스템)의 작동을 위한 중요한 수학 도구이며, 이더리움 애플리케이션에도 광범위하게 사용한다.

출판 시점 기준으로 이더리움 프로토콜의 어떤 부분도 암호화되어 있지 않다. 즉, 이더리움 플랫폼과 노드 간(트랜잭션 데이터 포함)의 모든 통신은 암호화되어 있지 않고, (따라서) 누구나 그 내용을 읽을 수 있다. 이렇게 해서 모든 사람이 상태 업데이트의 정확성을 확인할 수 있고, 합의에 도달할 수 있다. 향후에는 영 지식 증명(zero knowledge proof)과 동형 암호화(homomorphic encryption) 같은 고급 암호화 도구를 사용하여 여전히 합의를 가능하게 하면서도 암호화된 계산을 블록체인에 기록할 수 있을 것이다. 하지만 고급 암호화 도구를 제공할 준비는 마쳤으나 아직 배포되지는 않았다.

이 장에서는 이더리움에서 사용하는 암호 방식, 즉 개인키와 주소의 형태로 자금의 소유권을 제어하는 데 사용되는 공개키 암호화(Public Key Cryptography, PKC)를 소개한다.

1. 키와 주소

이더리움은 외부 소유 계정(Externally Owned Account, EOA)과 컨트랙트(contract)라는 두 가지 유형을 계정을 갖고 있다. 디지털 개인키(private key), 이더리움 주소(Ethereum address), 디지털 서명(digital signature)을 통해 외부 소유 계정의 이더 소유권을 확립한다. 개인키는 모든 사용자와 이더리움 간 상호작용의 핵심이다. 사실, 계정 주소는 개인키에서 직접 파생되고, 개인키는 계정(account)이라고도 불리는 단일 이더리움 주소를 고유하게 결정한다.

이더리움 시스템은 개인키를 이더리움에 전송하거나 저장하는 방식으로 직접 사용하지 않는다. 즉, 개인키는 비공개로 유지되어야 하고, 네트워크로 전달된 메시지에 나타나지 않으며, 체인에 저장되어서도 안 된다. 계정 주소와 디지털 서명만 이더리움 시스템에 전송되고 저장된다. 개인키는 안전하고 확실하게 보관해야 한다.

개인키를 사용하여 생성된 디지털 서명을 통해 자금의 접근과 통제가 이루어진다. 이더리움 트랜잭션은 유효한 디지털 서명이 블록체인에 있어야 한다. 개인키의 사본을 가진 사람은 누구나 해당 계정과 해당 계정이 가진 이더를 제어할 수 있다. 사용자가 자신의 개인키를 안전하게 유지한다면, 이더리움 트랜잭션의 디지털 서명은 개인키의 소유권을 증명하기 때문에 자금의 실제 소유자임도 증명한다.

이더리움에서 사용하는 것과 같은 공개키 암호화 기반 시스템에서 키는 개인(비밀)키와 공개키로 구성된 쌍으로 제공한다. 공개키는 은행 계좌 번호와, 개인키는 PIN(개인 식별 번호)과 유사하다고 생각해 보자. 후자는 계정에 대한 제어권을 제공하고, 전자를 가지고 계정을 식별할 수 있다. 개인키 자체는 이더리움 사용자에게 드러나는 경우가 거의 없다. 대부분 암호화된 형태로 특수 파일에 저장하고, 이더리움 지갑 소프트웨어로 관리한다.

이더리움 트랜잭션의 지급 부분에서 지정된 수신자는 이더리움 주소로 표시하며, 이 주소는 은행 송금의 수익자 계좌 세부 정보와 동일한 방식으로 사용한다. 이후에 자세히 볼 수 있듯이 외부 소유 계정의 이더리움 주소는 공개키-개인키 쌍의 공개키 부분에서 생성된다. 그러나 모든 이더리움 주소가 공개키-개인키 쌍을 나타내는 것은 아니다. 개인키로 뒷받침되지 않는 컨트랙트를 표시할 수도 있다.

2. 공개키 암호화와 암호화폐

공개키 암호화(비대칭 암호화라고도 함)는 오늘날 정보 보안의 핵심 요소다. 1970년대 마틴 헬먼(Martin Hellman), 휫필드 디피(Whitfield Diffie), 랄프 머클(Ralph Merkle)이 처음 공개한 이 기법은 암호학 분야에서 대중의 관심을 불러일으킨 기념비적인 돌파구였다. 70년대 이전에, 정부는 강력한 암호학 지식을 비밀로 유지했다.

공개키 암호화는 고유한 키를 사용하여 정보를 보호한다. 이 키는 특수한 속성(계산하기는 쉽지만 그 역(inverse)을 계산하기는 어렵다)을 가진 수학 함수를 바탕으로 한다. 이런 함수를 바탕으로한 암호화는 디지털 비밀과 위조 불가능한 디지털 서명을 만들 수 있으며, 이것은 수학 법칙에 의해 보장받는다.

예를 들어, 2개의 큰 소수를 곱하는 것은 아주 간단하다. 그러나 2개의 큰 소수의 곱을 감안할 때 소인수(소인수 분해(prime factorization)라고 하는 문제)를 찾는 문제는 매우 어렵다. 8,018,009라는 숫자가 두 소수의 결과라고 제시했을 때 그 두 소수를 찾는 것이 8,018,009를 만들기 위해 그 소수를 곱하는 것보다 훨씬 더 어렵다.

이런 수학 함수 중 일부는 비밀 정보를 알고 있을 때 쉽게 거꾸로 계산할 수 있다. 앞의 예에서 소인수 중 하나가 2,003이라고 하면, 간단히 나머지 소인수를 쉽게 찾을 수 있다(8,018,009 ÷ 2,003 = 4,003). 이런 함수는 역산하기 위한 단축키로 사용할 수 있는 비밀 정보가 없으면 거꾸로 계산하기 어렵기 때문에 트랩 도어 함수(trapdoor function)라고도 한다.

암호화에 유용한 수학 함수의 좀 더 발전된 범주는 타원 곡선의 산술 연산을 바탕으로 한다. 타원 곡선 산술에서 소수로 나눈 나머지를 곱하는 것은 간단하지만, 나눗셈(역함수)은 사실상 불가능하다. 이것을 이산 로그 문제(discrete logarithm problem)라고 하며, 현재는 알려진 트랩 도어는 없다. 타원 곡선 암호화(elliptic curve cyptography)는 최신 컴퓨터 시스템에서 광범위하게 활용되며, 이더리움(및 기타 암호화폐)에서 개인키와 디지털 서명을 사용하는 기초가 된다.

※ 페르마의 마지막 정리를 증명하는 과정에서 쓰였던 타원곡선이론은 현재 실생활에서 암호체계로써 많이 쓰이고 있다. 마국의 국가 안보국 NSA도 타원곡선암호 방식을 채택하고 있다. 타원곡선암호의 대표적인 장점은 공개키 암호방식에서 공개키 보다 짧은 키로써 비슷한 수준의 안전성을 제공한다는 것이다. 때문에 전송량이라던가 계산량이 제한된 무선환경들에서 그 장점이 부각된다. 교통카드, 신용카드, 의료보험증 등이 타원곡선암호체계를 이용하고 있고, 비트코인 또한 타원곡선암호 방식으로부터 만들어진 시스템이다.

암호학 WIKI

트랩 도어 함수 WIKI

소인수 분해

이산 로그

타원 곡선 암호화

이더리움에서는 공개키 암호화(비대칭 암호화라고도 함)를 사용하여 이 장에서 설명한 공개키-개인키 쌍을 만든다. 공개키는 개인키에서 파생되므로 '쌍'으로 간주한다. 그와 함께, 그 쌍은 공개적으로 접근할 수 있는 계정 핸들(주소)과 계정의 이더에 대한 접근 권한, 그리고 스마트 컨트랙트를 사용할 때 계정이 필요로 하는 모든 인증에 대한 사적 제어권을 제공함으로써 이더리움 계정을 나타낸다. 개인키는 계정에서 자금을 지출하기 위해 트랜잭션에 서명해야 하는 디지털 서명(digital signature)을 만드는 데 필요한 고유한 정보의 접근을 제어한다. 디지털 서명은 소유자 또는 컨트랙트 사용자를 인증하는 데도 사용한다.

대부분의 지갑 구현에서 개인키와 공개키는 편의상 키 쌍(key pair)으로 함께 저장한다. 그러나 공개키는 개인키로부터 간단히 계산될 수 있으므로 개인키만 저장하는 것도 가능하다.

디지털 서명을 만들어 모든 메시지에 서명할 수 있다. 이더리움 트랜잭션에서는 트랜잭션 자체의 세부사항이 메시지로 사용된다. 암호 수학(이번 예는 타원 곡선 암호화)은 메시지(즉, 트랜잭션 세부 정보)를 개인키와 결합하여 개인키를 알아야만 만들 수 있는 코드 생성 방법을 제공한다. 이 코드를 디지털 서명이라고 한다. 이더리움 트랜잭션은 기본적으로 특정 이더리움 주소로 특정 계정에 접근하는 요청이다. 자금을 이동하거나 스마트 컨트랙트와 상호작용하기 위해 트랜잭션을 이더리움 네트워크로 보내면, 문제의 이더리움 주소에 해당하는 개인키로 생성된 디지털 서명도 함께 보내야 한다. 타원 곡선 수학이란 디지털 서명, 트랜잭션 세부 정보, 접근하려는 이더리움 주소가 일치하는지 확인하여 '누구나' 트랜잭션이 유효한지 확인할 수 있음을 의미한다. 이러한 확인 과정에는 개인키가 전혀 포함되지 않는다. 개인키는 개인 영역에 남아 있다. 그러나 검증 프로세스에서는 의심의 여지 없이 그 트랜잭션이 공개키에 대응되는 개인키를 가진 사람에 의해 만들어졌음을 확증할 수 있다. 이것이 공개키 암호화의 '마법'이다.

이더리움 프로토콜에는 암호화가 없기 때문에, 이더리움 네트워크 동작의 일부로 보내는 모든 메시지는 모든 사람이 (불가피하게) 읽을 수 있다. 따라서 개인키는 트랜잭션 인증을 위한 디지털 서명을 만드는 데에만 사용한다.

3. 개인키

개인키는 단순히 무작위로 선택한 숫자다. 개인키의 소유권과 제어는 해당 주소를 승인하는 컨트랙트에 대한 접근뿐만 아니라 해당 이더리움 주소와 관련된 모든 자금에 대한 사용자 제어의 근원이다. 개인키는 트랜잭션에 쓰이는 자금의 소유권을 증명함으로써 이더를 소비하는데 필요한 서명을 만드는 데 사용된다. 개인키는 항상 비밀로 유지해야 한다. 왜냐하면 개인키를 제3자에게 공개하는 행위는 개인키로 확보한 컨트랙트와 이더에 대한 제어 권한을 제3자에게 부여하는 것이나 마찬가지이기 때문이다. 개인키는 반드시 백업하여 우발적인 손실로부터 보호해야 한다. 한번 잃어버리면 되찾을 수 없으며, 해당 키로 확보한 자금도 영원히 잃어버리게 된다.

이더리움 개인키는 숫자다. 비공개키를 무작위로 선택하는 방법 중 하나는 동전, 연필, 종이를 사용하는 것이다. 동전을 256번 던져서 이더리움 지갑에서 사용할 수 있는 2진수로 된 임의의 개인키를 얻을 수 있다. 공개키와 주소는 이 개인키로부터 생성될 수 있다.

3-1. 난수로 개인키 생성

키를 생성하는 가장 중요한 첫 번째 단계는 엔트로피, 즉 무작위성을 확보하는 것이다. 이더리움 개인키를 생성하는 것은 기본적으로 1에서 2^256 사이의 숫자를 선택하는 것이라고 볼 수 있다. 해당 번호를 선택하는 것이 예측 가능하거나 결정적이라면 이 번호 선택 방법은 중요해진다. 이더리움 소프트웨어는 기본 운영체제의 난수 생성기를 사용하여 256개의 임의 비트를 생성한다. 일반적으로 OS 난수 생성기는 사람이 무작위의 소스가 되어 초기화되므로 몇 초 동안 마우스를 움직이거나 키보드에서 임의의 키를 누르라는 요청을 받을 수 있다. 컴퓨터의 마이크로폰 채널에서 나오는 우주 방사선 노이즈가 대안이 될 수 있다.

좀 더 정확히 말하자면, 개인키는 2^256보다 약간 작은 0이 아닌 매우 큰 숫자(거대한 78자리 숫자, 대략 1.158 x 10^77)까지 가능하다. 정확한 숫자는 첫 번째 38자리를 2^256으로 공유하며, 이더리움에서 사용된 타원 곡선 순서로 정의한다. 비공개 키를 생성하기 위해 256비트 숫자를 무작위로 추출하여 유효한 범위 내에 있는지 확인한다. 프로그래밍 측면에서 이것은 일반적으로 더 큰 임의의 비트 문자열(암호학적으로 안전한 임의성 소스에서 수집됨)을 Keccak-256 또는 SHA-256 같은 256비트 해시 알고리즘에 공급함으로써 이루어 진다. 두 가지 알고리즘 모두 편리하게 256비트 수를 생성한다. 결과가 유효한 범위 내에 있으면 적절한 개인키가 된다. 그렇지 않으면 다른 임의의 숫자로 다시 시도하기만 하면 된다.

2^256(이더리움 개인키 공간 크기)은 대단히 큰 숫자다. 10진수로 약 10^77, 즉 77자리 숫자다. 비교를 해보자면, 우리가 보는 우주는 10^80개의 원자를 포함하는 것으로 추정된다. 따라서 우주에 있는 모든 원자에 이더리움 계정을 제공하기에 충분할 만큼의 개인키가 있다. 하나의 개인키를 무작위로 선택했을 때, 누군가가 그것을 추측하거나 스스로 같은 값을 선택할 수 있는 가능한 방법은 현재 없다.

개인키 생성 프로세스는 오프라인 프로세스다. 그것은 이더리움 네트워크와의 통신이나 다른 사람과의 통신을 필요로 하지 않는다. 따라서 아무도 선택할 수 없는 숫자를 선택하려면 그것은 정말로 무작위적이어야 한다. 만약 여러분이 직접 그 번호를 선택한다면, 다른 사람이 그것을 시도해서 같은 번호를 찾을 수 있는 확률이 너무 높다. 나쁜 난수 생성기(대부분의 프로그래밍 언어에 있는 의사 난수 rand 함수와 같은)를 사용하는 것은 복제하기가 훨씬 더 쉽기 때문에 더 나쁘다. 온라인 계정의 암호와 마찬가지로 개인키도 추측할 수 없어야 한다. 다행히도 개인키를 기억할 필요가 없으므로 가능한 한 최선의 접근 방식을 취할 수 있다. 즉, 진정한 무작위성이다.

임의의 숫자를 만들거나 프로그래밍 언어에서 제공하는 '간단한' 난수 생성기를 사용하는 코드는 작성하지 마라. 충분한 엔트로피 원천의 시드(seed)와 함께 암호로 안전한 의사 난수 생성기(예: CSPRNG)를 사용하는 것이 중요하다. 암호로 보호되어 있는지 확인하기 위해 사용하고자 하는 난수 생성기 라이브러리의 문서를 학습하라. CSPRNG 라이브러리의 올바른 구현은 키 보안에 중요하다.

다음은 임의로 생성한 16진수 형식의 개인키다(256비트는 64비트 16진수로 표시, 각 4비트).

f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315

4. 공개키

이더리움 공개키는 타원 곡선에 있는 점(point)으로 타원 곡선 방정식을 만족하는 x와 y 좌표의 집합을 의미한다.

더 간단한 용어로, 이더리움 공개키는 함께 결합된 2개의 숫자다. 이 숫자는 개인키로부터 단방향으로만 계산할 수 있다. 즉, 개인키가 있는 경우 공개키를 계산하기는 쉽지만, 공개키에서 개인키를 계산할 수는 없다.

공개키는 사실상 비가역적인 타원 곡선 곱셈을 사용하여 개인키로부터 계산된다. K = k * G, 여기서 k는 개인키, G는 생성자 점(generator point)이라고 불리는 상수점, K는 결과로 나오는 공개키, *는 특수 타원 곡선 곱하기 연산자다. 타원 곡선을 일반적인 곰셈과 같지 않다. 일반적인 곱셈과 기능적 속성을 공유하지만 그것뿐이다. 예를 들어, '이산 로그 찾기'(K를 알고 있는 경우 k를 계산한다)로 알려진 역 연산(정상 수에 대한 나눗셈)은 가능한 모든 k값을 시도하는 것만큼 어렵다(우주가 허용하는 것보다 더 많은 시간이 걸리는 무차별 대입 탐색).

간단히 말하면, 타원 곡선에 대한 산술 연산은 '정규'정수 연산과 다르다. 점(G)에 정수(k)를 곱하여 다른 점(K)을 생성할 수 있다. 그러나 나눗셈(division)같은 연산이 존재하지 않으므로 공개키 K를 G점으로 간단히 '나누어서' 개인키 k를 계산할 수 없다. 이것이 단방향 수학 함수다.

타원 곡선 곱셈은 암호학자가 '단방향'함수라고 부르는 함수 유형이다. 한 방향(곱하기)으로는 수행하기 쉽고 반대 방향(나누기)으로는 수행하기가 쉽지 않다. 개인키의 소유자는 아무도 함수를 되돌려서 공개키에서 개인키를 계산할 수 없다는 것을 알고 공개키를 쉽게 생성하여 세상과 공유할 수 있다. 이 수학적 트릭은 이더리움 자금의 소유권과 계약 관리를 입증하는 위조 불가능하고 안전한 디지털 서명의 기초가 된다.

4-1. 타원 곡선 암호화 설명

타원 곡선 암호화는 타원 곡선의 점에 더하기와 곱셈으로 표현되는 이산 대수 문제를 바탕으로 한 비대칭 또는 공개키 암호화 유형이다.

[그림 4-1]은 이더리움에서 사용하는 것과 비슷한 타원 곡선의 한 예다.

이더리움은 비트코인처럼 secp256k1이라는 정확한 타원 곡선을 사용한다. 따라서 비트코인의 타원 곡선 라이브러리 및 도구를 재사용할 수 있다.

[그림 4-1] 타원 곡선의 시각화

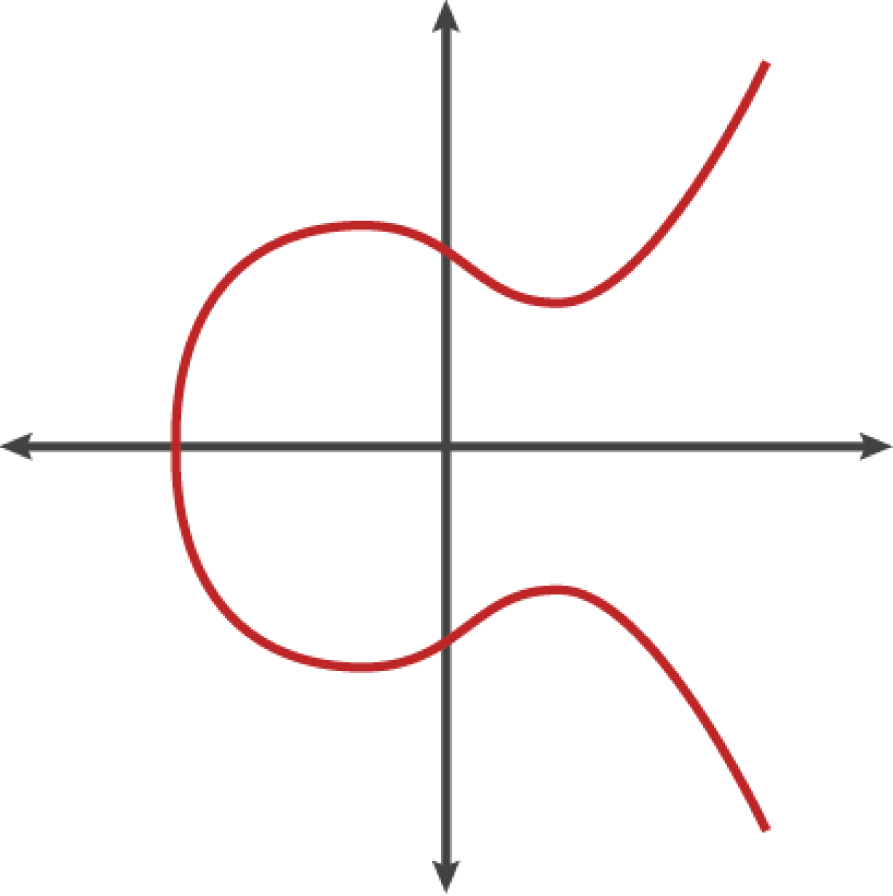
이더리움은 미국 표준기술연구소(National Institute of Standards and Technology, NIST)에서 제정한 secp256k1이라는 표준에 정의한 대로 특정 타원 곡선과 수학 상수 집합을 사용한다.

secp256k1 곡선은 타원 곡선을 생성하는 다음 함수로 정의한다.

y^2 = (x^3 + 7)over(𝔽 p)

또는

y^2 mod p = (x^3 + 7) mod p

mod p(소수 p로 나눈 나머지)는 이 곡선이 𝔽 p라고 쓰인 소수 차수 p의 유한체상에 있음을 나타낸다. 여기서 p = 2^256 – 2^32 – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1로, 매우 큰 소수다.

이 곡선은 실수 대신에 소수 위수의 유한체상에 정의했기 때문에 2차원으로 흩어져 있는 점들의 패턴처럼 보인다. 그래서 시각화하기 어렵다. 그러나 수학은 실수에 대한 타원 곡선 수학과 동일하다. 예를 들어, [그림 4-2]에서 보여주는 좌표 위의 점 패턴은 훨씬 작은 유한체인 소수 위수 17의 타원 곡선과 동일하다. secp256k1 이더리움 타원 곡선은 헤아릴 수 없을 만큼 큰 좌표에서 훨씬 더 복잡한 점 패턴으로 생각할 수 있다.

[그림 4-2] 타원 곡선 암호화 : p = 17일 때 F(p)에서 타원 곡선을 시각화

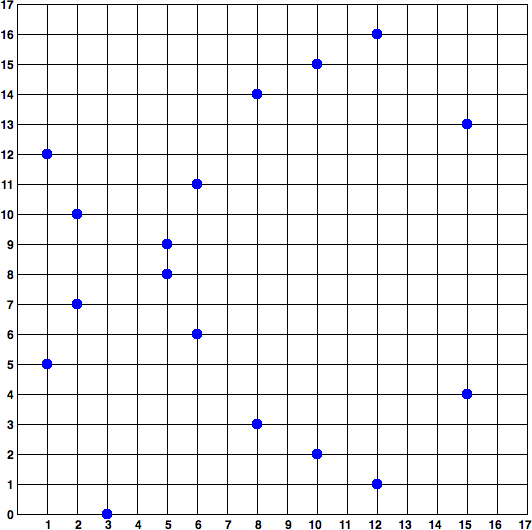
예를 들어, 다음은 secp256k1 곡선상의 점인 (x, y)를 갖는 점 Q이다.

Q =
(49790390825249384486033144355916864607616083520101638681403973749255924539515,
59574132161899900045862086493921015780032175291755807399284007721050341297360)

[예제 4-1]은 파이썬을 사용하여 직접 확인하는 방법이다. 변수 x와 y는 앞의 예와 같이 점 Q의 좌표다. 변수 p는 타원 곡선의 소수(모든 모듈로 연산에 사용되는 소수)다. 파이썬의 마지막 줄은 타원 곡선 방정식이다(파이썬의 % 연산자는 모듈러 연산자다). x와 y가 실제로 타원 곡선상의 한 점의 좌표라면, 그들은 방정식을 만족하고 결과는 0이다(0L은 값이 0이 긴 정수임). 커맨드라인에 python을 입력하고 목록에서 각 줄을 (>>> 프롬프트 다음에) 복사하여 직접 해보자.

[예제 4-1] 파이썬을 사용하여 이 점이 타원 곡선에 있음을 확인함

Python 3.4.0 (default, Mar 30 2014, 19:23:13)
[GCC 4.2.1 Compatible Apple LLVM 5.1 (clang-503.0.38)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> p = 115792089237316195423570985008687907853269984665640564039457584007908834 \
671663
>>> x = 49790390825249384486033144355916864607616083520101638681403973749255924539515
>>> y = 59574132161899900045862086493921015780032175291755807399284007721050341297360
>>> (x ** 3 + 7 - y**2) % p
0L

4-2. 타원 곡선 산술 연산

많은 타원 곡선 수학은 우리가 학교에서 배운 정수 산술과 매우 흡사하다. 특히 우리는 더하기 연산자를 정의할 수 있다. 이 연산자는 숫자 선을 따라 점프하는 대신 곡선의 다른 점으로 점프한다. 일단 우리가 덧셈 연산자를 가지면, 점의 정수의 곱셈을 정의할 수 있다. 이것은 반복되는 덧셈과 같다.

타원 곡선에 두 점 P1과 P2가 주어지면 세 번째 점 P3 = P1 + P2가 타원 곡선 위에 있도록 곡선 덧셈을 정의한다.

기하학적으로 이 세 번째 점 P3은 P1과 P2 사이의 선을 그려 계산한다. 이 선은 정확하게 하나의 추가 장소(놀랍게도)에서 타원 곡선과 교차한다. 이 점을 P3' = (x, y)라고 부르자. 이어서 x축에 반사하여 P3 = (x, -y)를 구한다.

P1과 P2가 같은 점이라면 P1과 P2 사이의 선은 이 점 P1에서 곡선에 대한 접선으로 확장되어야 한다. 이 접선은 정확히 하나의 새로운 점에서 곡선과 교차한다. 미적분 기법을 사용하여 접선의 기울기를 결정할 수 있다. 흥미롭게도 이 기술은 2차원 정수 좌표상에 있는 곡선 위의 점들에도 적용할 수 있다.

타원 곡선 수학에서는 무한대 점이라는 점도 있다. 이 점은 대략 숫자 0의 역할에 해당한다. 컴퓨터에서 x = y = 0으로 표시되는 예도 있다(타원 곡선 방정식을 만족하지는 않지만 쉽게 확인할 수 있다). 무한대 점의 필요성을 설명하는 몇 가지 특별한 예가 있다.

어떤 경우에는 (예를 들어, P1과 P2의 x값이 동일하고 y값은 다르다면) 선이 정확히 수직일 것이고, 이때 P3 = 무한대 점이 된다.

P1이 무한대 점이라면 P1 + P2 = P2이다. 이와 비슷하게, P2가 무한대 점이면 P1 + P2 = P1이다.

무한대 점이 '정상적인' 산술에서 0이 되는 것을 볼 수 있다.

+는 결합성이 있는 것으로 밝혀졌는데, 이것은 (A + B) + C = A + (B + C)를 의미한다. 즉, 모호함 없이 A + B + C(괄호 없이)를 쓸 수 있다.

앞에서 덧셈을 정의했으므로 덧셈을 확장하는 표준 방식으로 곱셈을 정의할 수 있다. 타원 곡선 상의 점 P에 대해 k가 정수이면 k * P = P + P + P + ... + P(k번 반복)이다. 이 경우에 k는 때때로(아마도 혼란스럽게) 지수(exponent)라고도 한다.

4-3. 공개키 생성

무작위로 생성한 숫자 k형태의 개인키로 시작하여 생성자 점(generator point) G라고 하는 곡선의 미리 결정된 점에 개인키를 곱하여 곡선 상의 다른 점, 즉 대응하는 공개키 K를 생성한다.

K = k * G

생성자 점은 secp256k1 표준의 일부로 지정되어 있다. secp256k1의 모든 구현에서 동일하며, 해당 곡선에서 파생된 모든 키는 동일한 점 G를 사용한다. 생성자 점은 모든 이더리움 사용자에 대해 항상 동일하기 때문에, G와 개인키 k를 곱한 결과는 항상 공개키 K로 동일하다. k와 K 사이의 관계는 고정되어 있지만, k에서 K까지 한 방향으로만 계산할 수 있다. 이런 이유로 이더리움 주소(K에서 파생됨)를 모든 사람과 공유할 수 있으며 사용자의 개인키(k)는 공개하지 않는다.

앞에서 설명했듯이, k * G의 곱셈은 반복되는 덧셈, 즉 G + G + G + ... + G(k번 반복)와 동일하다. 요약하면, 개인키 k로부터 공개키 K를 생성하기 위해 생성자 점 G를 그 자체에 k번 추가한다.

개인키는 공개키로 변환할 수 있지만 공개키는 개인키로 다시 변환할 수 없다. 이는 수학이 한 방향으로만 작동하기 때문이다.

4-4. 특정 개인키의 공개키를 찾아내는 예제

K = f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315 * G

암호화 라이브러리는 타원 곡선 곱셈을 사용하여 K를 계산하는 데 도움이 된다. 결과 공개키 K는 다음과 같은 점으로 정의한다.

K = (x, y)

여기서

x = 6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b
y = 83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0

이더리움에서는 16진수 문자(65바이트) 130개의 시리얼라이제이션(serialization)으로 표시되는 공개키를 볼 수 있다. 이것은 업계 표준인 능률 암호화 표준(Standards for Efficient Cryptography 1, SEC 1)에서 문서화된 산업 컨소시엄 능률 암호 그룹 표준(Standards for Efficient Cryptography Group, SEGC)이 제안한 표준 시리얼라이제이션 형식에서 채택했다. 이 표준은 아래 표에 나열된 타원 곡선의 점을 식별하는 데 사용할 수 있는 네 가지 가능한 접두어를 정의한다.

시리얼라이즈된 EC 공개키 접두어

접두어	의미	길이(접두어 바이트 수)
0x00	무한대를 가리킴	1
0x04	압축되지 않은 지점	65
0x02	짝수 y의 암축된 점	33
0x03	홀수 y의 압축된 점	33

이더리움은 압축되지 않은 공개키만을 사용한다. 따라서 관련된 유일한 접두어는 (16진수)04이다. 시리얼라이제이션은 공개키의 x와 y좌표를 연결한다.

04 + x좌표(32바이트/64(16진수)) + y좌표(32바이트/64(16진수))

따라서 이전에 계산한 공개키는 다음과 같이 시리얼라이즈된다.

046e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0 \
c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0

4-5. 타원 곡선 라이브러리

암호화폐와 관련된 프로젝트에 사용되는 secp256k1 타원 곡선을 구현한 것이 몇 가지 있다.

OpenSSL

OpenSSL 라이브러리는 secp256k1의 전체 구현을 포함하여 포괄적인 암호학적 기반 요소(primitive)를 제공한다. 예를 들어, 공개키를 생성하려면 EC_POINT_mul 함수를 사용할 수 있다.

libsecp256k1

비트코인 코어(Bitcoin Core)의 libsecp256k1은 타원 곡선 및 기타 암호화 기초 요소를 C 언어로 구현한 것이다. 비트코인 코어 소프트웨어에서 OpenSSL을 대체하기 위해 완전히 새로 작성했으며, 성능과 보안 면에서 모두 뛰어난 것으로 여겨진다.

5. 암호화 해시 함수

암호화 해시 함수(hash function)는 이더리움 전반에 걸쳐 사용된다. 사실, 해시 함수는 거의 모든 암호학적 시스템에서 광범위하게 사용되고 있다. 이것은 암호학자 브루스 슈나이어(Bruce Schneier)도 동의한 사실인데, 그는 이렇게 말했다. "암호화 알고리즘보다 단방향 해시 함수들이 현대 암호학을 더 잘 이끄는 견인차다."

이 절에서는 해시 함수에 대해 논의하고, 기본 속성을 탐색하며, 이러한 속성을 어떻게 현대 암호학 분야에서 매우 유용하게 사용하는지 살펴본다. 이더리움 공개키 주소로 변환하는 작업에서 해시 함수가 일부분을 차지하기 때문에 여기에서 해시 함수를 다룬다. 또한 데이터 확인에 도움이 되는 디지털 지문(digital fingerprints)을 만드는 데 사용할 수 있다.

간단히 말하면, 해시 함수(hash function)는 '임의 크기의 데이터를 고정된 크기의 데이터로 매핑하는 데 사용할 수 있는 모든 함수'다. 해시 함수에 대한 입력을 사전 이미지(pre-image), 메시지(message) 또는 입력 데이터(input data)라고 한다. 그리고 그 결과를 해시(hash)라고 한다. 암호화 해시 함수(cryptographic hash function)는 이더리움 같은 플랫폼을 보호하는 데 유용한 특정 속성을 갖는 특별한 하위 범주다.

암호 해시 함수는 임의 크기의 데이터를 고정 크기의 비트 열로 매핑하는 단방향(one-way) 해시 함수다. '단방향' 특성은 결괏값 해시만 알고 있을 때 입력 데이터를 다시 작성하는 것이 계산적으로 불가능함을 의미한다. 가능한 입력을 결정하는 유일한 방법은 각 후보에 일치하는 결과가 있는지 확인하면서 무차별 대입 검색을 수행하는 것이다. 검색 공간이 사실상 무한하다는 점을 고려할 때 작업이 실제로 불가능하다는 것을 쉽게 이해할 수 있다. 일치하는 해시를 만드는 일부 입력 데이터를 찾는다고 하더라도 원본 입력 데이터가 아닐 수 있다. 해시 함수는 '다대일' 함수다. 동일한 결과에 해시 처리한 두 입력 데이터 집합을 찾는 것을 해시 충돌(hash collision) 찾기라고 한다. 간단히 말해서, 해시 함수가 좋을수록 해시 충돌이 덜 발생한다. 이더리움에서는 사실상 해시 충돌이 불가능하다.

암호화 해시 함수의 주소 속성을 자세히 살펴보자.

결정론(determinism)

주어진 입력 메시지는 항상 동일한 해시 결과를 생성한다.

검증성(verifiability)

메시지의 해시 계산은 효율적이다(선형 복잡성).

비상관성(noncorrelation)

메시지에 대한 작은 변화(예: 1비트 변경)는 해시 출력을 너무 광범위하게 변경해야 해서 원본 메시지의 해시과 상관 관계가 없다.

비가역성(irreversibility)

해시로부터 메시지를 계산하는 것은 불가능하다. 모든 가능한 메시지에 대한 무차별 검색(brute-force search)과 같다.

충돌 방지(collision protection)

같은 해시 결과를 생성하는 2개의 서로 다른 메시지를 계산하는 것은 불가능하다.

해시 충돌에 대한 저항은 특히 이더리움에서 디지털 서명 위조를 피하기 위해 중요하다.

이러한 속성을 조합하면 암호화 해시 기능이 다음과 같은 다양한 보안 애플리케이션에 유용하다.

데이터 핑거프린팅
메시지 무결성(오류 감지)
작업증명
인증(암호 해싱 및 스트래칭)
의사 난수 생성기
메시지 커밋(커밋-공개 메커니즘)
고유 식별자

5-1. 이더리움 암호화 해시 함수 : Keccak-256

이더리움은 많은 곳에서 Keccak-256 암호화 해시 함수를 사용한다. Keccak-256은 2007년 국립 과학 기술 연구소(National Institute of Science and Technology)에서 개최한 SHA-3 암호화 해시 함수 경쟁 대회(SHA-3 Cryptographic Hash Function Competition)의 후보로 설계되었다. Keccak은 우승한 알고리즘으로, 2015년 FIPS(Federal Information Processing Standard) 202로 표준화되었다.

그러나 이더리움을 개발하는 기간 동안 미국 표준기술연구소(NIST)의 표준화는 아직 완료되지 않았다. NIST의 주장에 따르면, 표준 프로세스를 완료한 후 Keccak의 일부 파라미터를 조정하여 효율성을 향상했다고 한다. 하지만 이것은 미국 국가안보국(National Security Agency)의 부적절한 영향을 받아 Dual_EC_DRBG 난수 생성기 표준을 의도적으로 약화시켜 표준 난수 생성기에 백도어를 효과적으로 배치했다는 문서를 내부 고발자인 에드워드 스노든(Edward Snowden)이 공개했다. 이 논쟁의 결과는 제안한 변경에 대한 반발로 인해 SHA-3의 표준화에 상당한 지연을 초래했다. 당시 이더리움 재단은 NIST에서 수정한 SHA-3 표준이 아닌, 이 알고리즘의 발명가들이 제안한 대로 원래 Keccak 알고리즘을 구현하기로 결정했다.

이더리움 문서와 코드에서 언급된 'SHA-3'을 볼 수도 있지만, 실제로 모든 예는 아니더라도 많은 것이 FIPS-202 SHA-3 표준이 아닌 Keccak-256을 참고한다. 구현 차이는 패딩 파라미터와 관련하여 미미하지만, Keccak-256이 동일한 입력에 대해 FIPS-202 SHA-3과는 다른 해시 결과를 생성한다는 점에서 중요하다.

5-2. 어떤 해시 함수를 사용하고 있는가?

두 소프트웨어 모두 SHA-3이라면, 사용 중인 소프트웨어 라이브러리가 FIPS-202 SHA-3 또는 Keccak-256을 구현하는지 어떻게 알 수 있는가?

쉽게 알 수 있는 방법은 주어진 입력에 대해 예상되는 결과인 테스트 벡터(test vector)를 사용하는 것이다. 해시 함수가 가장 일반적으로 사용되는 테스트는 빈 입력(empty input)이다. 빈 문자열을 입력으로 해시 함수를 실행하면 다음과 같은 결과가 나온다.

Keccak256("") =
  c5d2460186f7233c927e7db2dcc703c0e500b653ca82273b7bfad8045d85a470

SHA3("") =
  a7ffc6f8bf1ed76651c14756a061d662f580ff4de43b49fa82d80a4b80f8434a

함수가 무엇인지에 관계없이 이 간단한 테스트를 실행하여 원래 Keccak-256인지 또는 최종 NIST 표준 FIPS-202 SHA-3인지 여부를 테스트할 수 있다. 이더리움은 코드에서 종종 SHA-3이라고 불리기는 하지만 Keccak-256을 사용한다.

이더리움(Keccak-256)과 최종 표준(FIP-202 SHA-3)에서 사용한 해시 함수의 차이로 인해 혼란이 있기 때문에 모든 코드, 연산코드(opcode) 및 라이브러리 sha3 인스턴스를 모두 keccak256으로 개명하기 위한 노력이 진행중이다. ERC59

다음으로 이더리움에서 Keccak-256의 첫 번째 애플리케이션을 살펴보자. 이 애플리케이션은 공개키로 이더리움 주소를 생성하는 것이다.

6. 이더리움 주소

이더리움 주소는 Keccak-256 단방향 해시 함수를 사용하는 공개키 또는 컨트랙트에서 파생한 고유 식별자(unique identifier)다.

이전 예제에서는 개인키로 시작해서 타원 곡선 곱셈을 사용하여 공개키를 만들었다.

개인키 : k

k = f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315

공개키 K (x 및 y 좌표가 연결되고 16진수로 표시됨)

K = 6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e...

주소를 계산할 때 공개키가 접두어(16진수) 04로 포맷되지 않았다는 사실은 주목할 만한 가치가 있다.

Keccak-256을 사용하여 이 공개키의 해시를 계산한다.

Keccak256(K) = 2a5bc342ed616b5ba5732269001d3f1ef827552ae1114027bd3ecf1f086ba0f9

그런 다음, 이더리움 주소인 마지막 20바이트(최하위 바이트)만 유지한다.

001d3f1ef827552ae1114027bd3ecf1f086ba0f9

종종 이더리움 주소가 접두어 0x로 표시되어 다음과 같이 16진수로 인코딩된 것을 볼 것이다.

0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9

6-1. 이더리움 주소 형식

이더리움 주소는 16진수이며, 공개키 Keccak-256 해시의 마지막 20바이트에서 파생한 식별자다.

모든 클라이언트의 사용자 인터페이스에 내장된 체크섬을 포함하여 잘못 입력된 주소를 보호하도록 인코딩된 비트코인 주소와 달리 이더리움 주소는 체크섬이 없는 원시 16진수로 표시한다.

그 결정의 근거는 이더리움 주소가 결국 시스템의 상위 계층에서 추상화(예: 이름 서비스)에 숨겨지고 필요하다면 상위 계층에 체크섬을 추가해야 한다는 것이다.

현실적으로 이러한 상위 계층은 너무 느리게 개발되었으며, 이러한 설계 선택은 잘못 입력한 주소 및 입력 유효성 오류로 인한 자금 손실 등 생태계 초기에 여러 가지 문제를 발생시켰다. 또한 이더리움 이름 서비스가 처음 예상보다 느리게 개발되었기 때문에 지갑 개발자는 대체 인코딩을 매우 천천히 채택했다. 다음으로 인코딩 옵션 몇 가지를 살펴보자.

6-2. 클라이언트 주소 상호교환 프로토콜

클라이언트 주소 상호교환 프로토콜(Inter exchange Client Address Protocol, ICAP)은 국제 은행 계좌 번호(International Bank Account Number, IBAN) 인코딩과 부분적으로 호환되는 이더리움 주소 인코딩으로, 이더리움 주소에 대해 다목적의 체크섬이 가능하고 상호운용 가능한 인코딩을 제공한다. ICAP 주소는 이더리움 이름 레지스트리에 등록한 이더리움 주소 또는 일반 이름을 인코딩할 수 있다. 이더리움 위키에 ICAP에 대해 더 많은 정보가 있다.

IBAN은 은행 계좌 번호를 식별하기 위한 국제 표준으로 주로 은행 송금에 사용하며, 유럽 단일 유로 지급 지역(Single Euro Payments Area, SEPA) 및 그 이상 지역에서 광범위하게 채택된다. IBAN은 중앙 집중적이고 엄격하게 규제되는 서비스다. ICAP는 탈중앙화형이지만 이더리움 주소에 대한 호환 가능하다.

IBAN은 국가 코드, 체크섬 및 은행 계좌 식별자(국가별)를 포함하는 최대 34개의 영숫자(대소문자를 구분하지 않음)로 구성된 문자열로 구성한다.

ICAP는 이더리움을 나타내는 비표준 국가 코드 XE를 도입한 후에 두 문자 체크섬과 계정 식별자의 세 가지 가능한 변형을 도입하여 동일한 구조를 사용한다.

직접(Direct)

이더리움 주소의 최하위 비트 155개를 나타내는 최대 30자의 영숫자로 구성된 빅엔디안(big-endian) base36 정수다. 이 인코딩은 일반 이더리움 주소의 전체 160비트보다 적기 때문에 하나 이상의 0바이트로 시작하는 이더리움 주소에서만 동작한다. 장점은 필드 길이와 체크섬 측면에서 IBAN과 호환된다는 것이다.

예: XE60HAMICDXSV5QXVJA7TJW47Q9CHWKJD (33자 길이)

기본(Basic)

직접 인코딩과 동일하지만 길이는 31자다. 이렇게 하면 이더리움 주소를 인코딩할 수 있지만 IBAN 필드 유효성 검사와 호환되지 않는다.

예: XE18CHDJBPLTBCJ03FE9O2NS0BPOJVQCU2P (35자 길이)

간접(Indirect)

이름 레지스트리 공급자를 통해 이더리움 주소로 확인되는 식별자를 인코딩한다. 자산 식별자(asset identifier, 예: ETH), 이름 서비스(예: XREG) 및 사람이 읽을 수 있는 9자의 이름(예: KITTYCATS)으로 구성된 16개의 영숫자를 사용한다.

예: XE##ETHXREGKITTYCATS (20자 길이)

여기서 ##는 2개의 계산된 체크섬 문자로 대체해야 한다.

helpeth 커맨드 라인 도구를 사용하여 ICAP 주소를 만들 수 있다. 예제로 개인키를 만들어 보자(0x로 접두어를 붙이고, 파라미터를 helpeth로 전달함).

$ helpeth keyDetails \
  -p 0xf8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315

Address: 0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9
ICAP: XE60 HAMI CDXS V5QX VJA7 TJW4 7Q9C HWKJ D
Public key: 0x6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b...

helpeth 명령은 ICAP 주소뿐만 아니라 16지수 이더리움 주소를 만든다. 예제 키의 ICAP 주소는 다음과 같다.

XE60HAMICDXSV5QXVJA7TJW47Q9CHWKJD

예제 이더리움 주소는 0바이트로 시작하기 때문에 IBAN 형식으로 유효한 직접(Direct) ICAP 인코딩 방법을 사용하여 인코딩할 수 있다. 이것은 길이가 33자라는 점에서 알아차릴 수 있다.

주소가 0으로 시작하지 않으면 기본(Basic) 인코딩으로 인코딩한다. 길이는 35자이고 IBAN은 유효하지 않다.

0바이트로 시작하는 이더리움 주소의 확률은 256분의 1이다. 이런 것을 생성하려면 IBAN과 호환 가능한 '직접(Direct)' 인코딩된 ICAP 주소로 작동하는 것을 찾기 전에 256개의 다른 임의의 개인키로 평균 256번을 시도해야 한다.

현재 ICAP는 불행히도 몇 가지 지갑에만 지원한다.

6-3. 대문자로 16진수 인코딩된 체크섬(EIP-55)

ICAP와 네임 서비스의 느린 배포 때문에 이더리움 개선 제안(Ethereum Improvement Proposal 55, EIP-55)에서 표준을 제안했다. EIP-55는 16진수 주소의 대소문자를 수정하여 이더리움 주소에 대해 이전 버전과 호환되는 체크섬을 제공한다. 이더리움 주소는 대소문자를 구분하지 않으며, 모든 지갑은 해석의 차이 없이 대문자 또는 소문자로 표현된 이더리움 주소를 수용해야 한다는 것이다.

주소의 알파벳 대소문자를 수정함으로써 입력의 무결셩을 보호하기 위해 사용할 수 있는 체크섬을 전달할 수 있다. EIP-55 체크섬을 지원하지 않는 지갑은 주소에 대문자가 혼용된다는 사실을 무시하지만, 이를 지원하는 사용자는 주소를 확인하고 99.986%의 정확도로 오류를 감지할 수 있다.

혼합 대문자 인코딩은 미묘하기 때문에 처음에는 인식하지 못할 수도 있다. 예제 주소는 다음과 같다.

0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9

EIP-55 혼합 대문자 체크섬을 사용하면 다음과 같이 된다.

0x001d3F1ef827552Ae1114027BD3ECF1f086bA0F9

16진수 인코딩 알파벳의 일부 알파벳(A~F) 문자는 대문자인 반면, 그 밖의 문자는 소문자다.

EIP-55는 구현하기 쉽다. 소문자 16진수 주소의 Keccak-256 해시를 사용하는데, 이 해시는 주소의 디지털 지문 역할을 하며 편리한 체크섬을 제공한다. 입력(주소)이 조금만 변경되면 결과 해시(체크섬)가 크게 변경되어 오류를 효과적으로 감지할 수 있다. 그러면 주소의 해시가 주소 자체의 대문자로 인코딩된다. 단계별로 나누어보자.

0x 접두어 없이 소문자 주소를 해시 처리한다.

Keccak256("001d3f1ef827552ae1114027bd3ecf1f086ba0f9") =
23a69c1653e4ebbb619b0b2cb8a9bad49892a8b9695d9a19d8f673ca991deae1

해시의 해당 16진수가 0x8 이상인 경우 각 알파벳 문자를 대문자로 만들어라. 주소와 해시를 정렬하면 표시하기가 더 쉽다.

Address: 001d3f1ef827552ae1114027bd3ecf1f086ba0f9
Hash   : 23a69c1653e4ebbb619b0b2cb8a9bad49892a8b9...

우리 주소에는 네 번째 위치에 알파벳 문자 d가 들어 있다. 해시의 네 번째 문자는 6보다 작다. 따라서 d는 소문자로 남겨둔다. 우리 주소의 다음 알파벳 문자는 여섯 번째 위치에 있는 f이다. 16진수 해시의 여섯 번째 문자는 c보다 크고 8이다. 따라서 주소에서 F를 대문자로 변환하는 식이다. 보다시피, 해시의 처음 20바이트(40자의 16진수)만 체크섬으로 사용한다. 주소에 20바이트(40자의 16진수)가 적절하게 대문자로 되어 있기 때문이다.

결과로 나온 혼합 대문자를 직접 확인하고, 대문자로 된 문자와 주소 해시에 해당하는 문자를 알 수 있는지 확인해 보자.

Address: 001d3F1ef827552Ae1114027BD3ECF1f086bA0F9
Hash   : 23a69c1653e4ebbb619b0b2cb8a9bad49892a8b9...

EIP-55로 인코딩된 주소의 오류 감지

이제 EIP-55 주소가 오류를 찾는 데 어떻게 도움이 되는지 살펴보자. EIP-55로 인코딩된 이더리움 주소를 인쇄했다고 가정해 보자.

0x001d3F1ef827552Ae1114027BD3ECF1f086bA0F9

이제 그 주소를 읽는 데 있어 기본적인 실수를 해보자. 마지막 문자 이전의 문자는 대문자 F이다. 이 예시에서는 그 문자를 대문자 E로 잘못 읽었다고 가정하고 다음 (잘못된) 주소를 지갑에 입력한다.

0x001d3F1ef827552Ae1114027BD3ECF1f086bA0E9

다행히도 지갑은 EIP-55를 준수한다. 대소문자가 혼용됐음을 확인하고 주소의 유효성을 검사한다. 소문자로 변환하고 체크섬 해시를 계산한다.

Keccak256("001d3f1ef827552ae1114027bd3ecf1f086ba0e9") =
5429b5d9460122fb4b11af9cb88b7bb76d8928862e0a57d46dd18dd8e08a6927

보다시피, 주소가 한 문자씩 변경되더라도(사실 e와 f가 1비트씩 떨어져 있기 때문에 실제로는 한 비트만 사용됨) 주소의 해시가 급격하게 변경되었다. 이것은 체크섬에 유용하게 쓸 수 있는 해시 함수의 속성이다.

이제 두 가지를 정리하고 대문자를 확인해 보자.

001d3F1ef827552Ae1114027BD3ECF1f086bA0E9
5429b5d9460122fb4b11af9cb88b7bb76d892886...

모두 잘못됐다. 알파벳 문자 중 일부가 대문자로 잘못 표시되었다. 대소문자는 '올바른' 체크섬의 인코딩임을 기억하자.

입력한 주소의 대문자 사용은 계산된 체크섬과 일치하지 않으므로 주소가 변경되어 오류가 발생했다.

7. 결론

이 장에서는 공개키 암호화를 간략하게 살펴보고, 이더리움에서 공개키 및 개인키 사용과 해시 함수 같은 암호화 도구를 사용하여 이더리움 주소를 만들고 검정하는 데 중점을 두었다. 또한 디지털 서명과 개인키를 공개하지 않고 개인키의 소유권을 입증할 수 있는 방법에 대해서도 살펴봤다.

개발새발

블록체인 개발 어때요

이전 포스트

Mastering Ethereum 3

다음 포스트

Mastering Ethereum 4