백준 2225 / 합분해

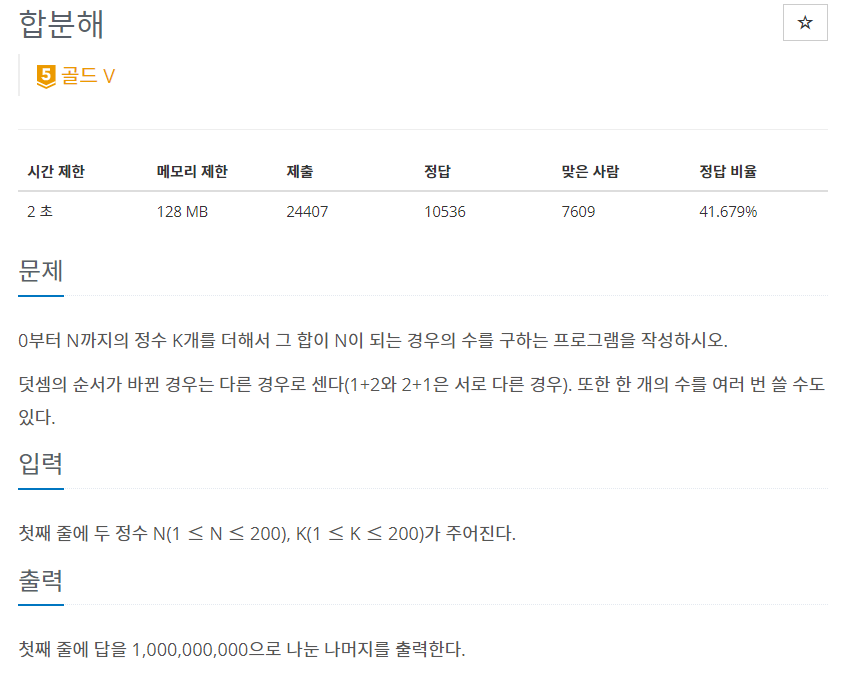
문제

풀이

설명

1,2,3 더하기와 비슷한 문제이다.
0부터 N까지의 정수 K개를 더해서 그 합이 N이 되는 경우의 수를 구한다.

D[k][N]=0부터 N까지의 정수 K개를 더해서 그 합이 N이 되는 경우의 수

? + ? + ? + ? + … + ? + L = N
위의 식이 나타내는 값: D[K][N]
? + ? + ? + ? + … + ? = N-L
위의 식이 나타내는 값: D[K-1][N-L]
• D[K][N] = ΣD[K-1][N-L] (0 ≤ L ≤ N)

코드

 public static long mod = 1000000000L;
    public static void main(String args[]) {
    
        Scanner sc = new Scanner(System.in);
        
        int n = sc.nextInt();
        int k = sc.nextInt();
        long[][] d = new long[k+1][n+1];
        d[0][0] = 1;
        
        for (int i=1; i<=k; i++) {
            for (int j=0; j<=n; j++) {
                for (int l=0; l<=j; l++) {
                    d[i][j] += d[i-1][j-l];
                    d[i][j] %= mod;
                }
            }
        }
        System.out.println(d[k][n]);
    }

코드설명

참고 :
출처 : https://www.acmicpc.net/problem/2225