[Cryptography 3.] Elliptic Curve에 대하여

DoHoon Kim·2022년 5월 4일

Cryptography

목록 보기

4/6

이때까지 public key system의 2가지 예시인 RSA system과 ElGamal system에 대해 살펴보았습니다.

RSA system과 ElGamal system에는 여러 단점들이 존재했고, 특히 컴퓨터의 연산 능력이 점차 발전함에 따라 암호 체계를 방어하기 위해 더 긴 암호문을 생성해야만 했습니다. 이는 암호화 자체에서 부하가 걸리게끔 만들었고, 결국은 새로운 암호 체계의 필요성이 부각됐습니다. 기존의 암호 시스템들과 암호화에 드는 비용이 비슷하면서, 더 높은 보안 강도를 제공하는 암호 시스템이 필요해졌고, 이로 인해 등장한 것이 타원곡선암호(Elliptic curve cryptography)입니다.

이번 포스트에서는 타원곡선에 대해 먼저 소개하겠습니다.

타원곡선에 대하여

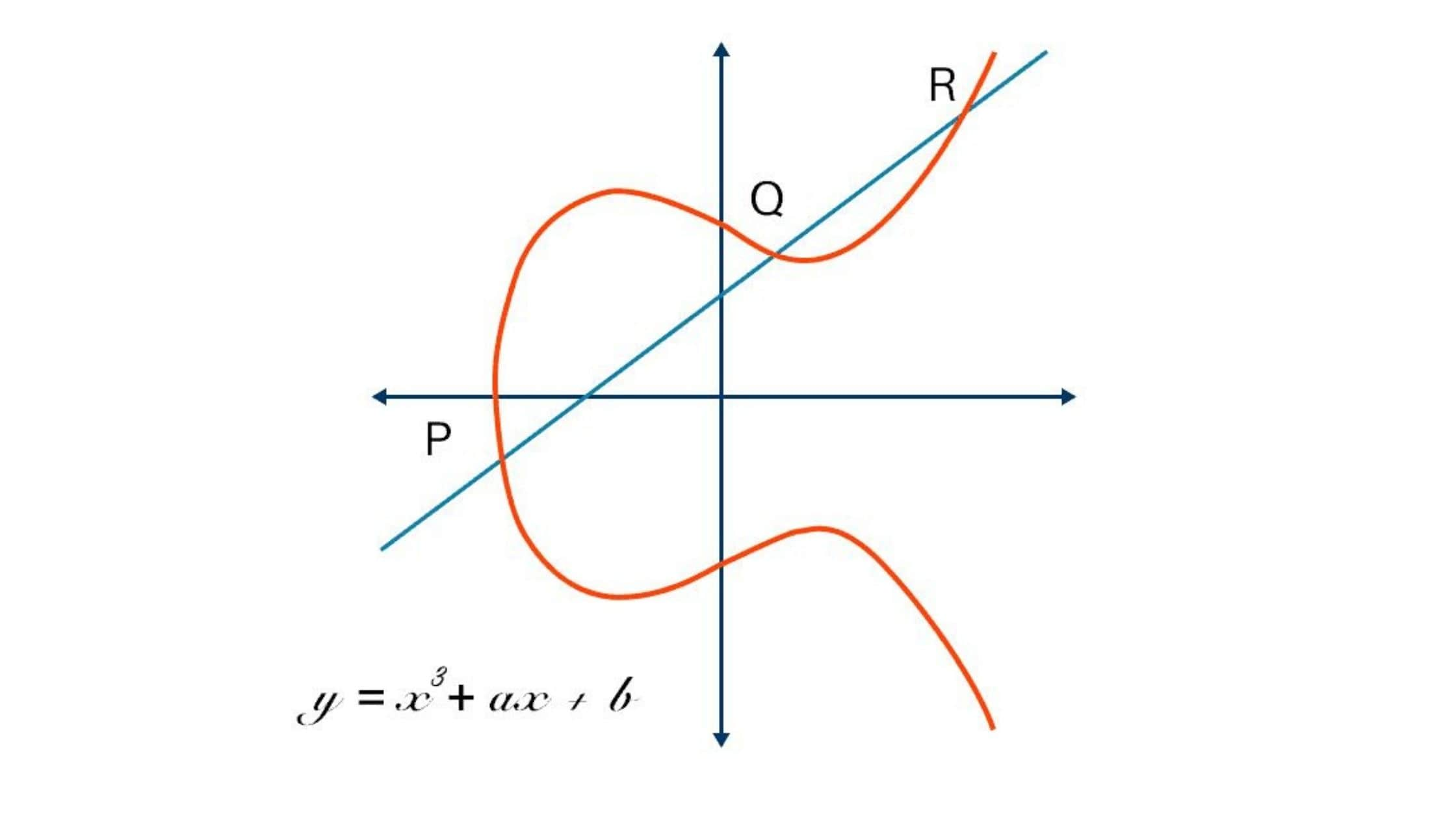
타원곡선암호에 대해 살펴보기에 앞서, 타원곡선에 대해 알아보겠습니다. 타원곡선은 다음 방정식을 만족하는 점들의 집합입니다.

y^{2} \;= \;x^{3} \;+ax \;+ \;b \\ 4a^{3} \;+ \;27b^{2} \;\not= \;0

이는 Weierstrass normal form 으로 불립니다. $4a^{3} \;+ \;27b^{2} \;\not= \;0$ 은 타원곡선 상에 singular point가 존재하지 않기 위한 필요충분조건입니다.
위 식에서 알 수 있듯이, 타원곡선은 x-축에 대해 대칭임을 알 수 있습니다.

실수체에서 정의된 타원곡선

위의 정의를 확장해서 무한원점(point at infinity)라는 가상의 점을 추가하겠습니다. 실수체 상에서 타원곡선은 다음과 같이 정의됩니다.

\{(x, \;y) \in (\real)^{2} \;| \;y^{2} \equiv \;x^{3} \;+ax \;+b \pmod {p}, \\ \qquad\qquad\qquad\qquad\quad\; 4a^{3} \;+ \;27b^{2} \not\equiv \;0 \pmod {p} \} \;\cup \; \{0\}

이렇게 타원곡선을 정의하게 되면, 타원곡선 상의 점들은 점들의 덧셈에 대해 닫혀있는 abelian group 을 형성하게 됩니다. 그럼 타원곡선 상에서 점들의 덧셈은 어떻게 정의되는 것일까요?

타원곡선 상의 점들의 덧셈

타원곡선 상의 점들의 덧셈은 다음과 같은 규칙이 성립합니다.

Given \;three \;aligned, \;non \;zero \;points \;P, \;Q \;and \;R, \\ \;P \;+Q \;+R \;= \;0

좀 더 자세하게 알아보겠습니다.

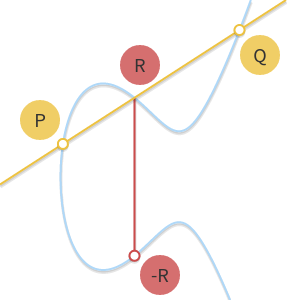
타원곡선 상에서 점들의 덧셈 $P \;+ \;Q$ 의 결과는 $P, \;Q$ 를 연결하는 직선과 타원곡선의 교점 $R$ 을 x-축에 대해 대칭한 점입니다.

만약 $P, \;Q$ 가 x-축에 대해 대칭이면 덧셈 결과는 어떻게 될까요? $P, \;Q$ 를 연결하는 직선은 x-축에 대해 수직이기 때문에, 타원곡선과 $P, \;Q$ 외의 점에서 만나지 않습니다. 이런 경우 $P \;+ \;Q \;= \;0$ 으로 정의합니다. $P, \;Q$ 가 x-축에 대해 대칭인 경우 두 점의 덧셈 결과는 무한원점이 됩니다.

만약 $P$ 와 $Q$ 가 같다면 어떻게 될까요? 이 때 $P, \;Q$ 를 타원곡선 상에서 무한히 가까운 점이라고 생각한다면, $P, \;Q$ 를 연결하는 직선은 타원곡선 상의 점 $P$ 에 접하는 직선이라고 생각할 수 있습니다. 따라서 점들의 덧셈 결과는 타원곡선의 점 $P$ 에 접하는 접선과의 교점이 됩니다.

타원곡선 상에서 정의되는 군(group)

타원곡선 상의 점들은 위에서 정의한 점들의 덧셈에 대해 군(group)을 형성하게 됩니다. 추가적으로, 타원곡선 상에서 점들의 덧셈은 교환법칙(commutative law)를 만족하기 때문에 abelian group을 형성합니다.

군(group) $(G, \;+)$ 는 다음과 같이 정의됩니다.

$G$ 는 연산 $+$ 에 대해 닫혀 있다.

연산 $+$ 는 associative하다.

$G$ 에 연산 $+$ 에 대한 unique한 항등원이 존재한다.

$G$ 의 모든 원소에 대해 unique한 역원이 존재한다.

타원곡선에서 점들의 덧셈에 대한 항등원은 무한원점(point of infinity)이고, non-zero point에 대한 역원은 x-축에 대해 대칭한 점입니다.

유한체에서 정의된 타원곡선

이번에는 유한체에서 정의된 타원곡선에 대해 살펴 보겠습니다. 유한체란 원소의 개수가 유한한 체를 말합니다.

유한체의 가장 간단한 예시로는 소수 $p$ 에 대해, $\mod {p}$ 에 대한 정수들의 집합으로 생각할 수 있습니다. $\{0, \;1, \;2, ..., \;p \;- \;1\}$ 과 $\mod {p}$ 에 대해 정의된 덧셈, 곱셈이 이루는 체를 $F_{p}$ 로 명시하겠습니다.

유한체 $F_{p}$ 상에서 타원곡선은 다음과 같이 정의됩니다.

\{(x, \;y) \in (F_{p})^{2} \;| \;y^{2} \equiv \;x^{3} \;+ax \;+b \pmod {p}, \\ \qquad\qquad\qquad\qquad\quad\;\; 4a^{3} \;+ \;27b^{2} \not\equiv \;0 \pmod {p} \} \;\cup \; \{0\}

타원곡선 상에서 점들의 덧셈

유한체 상에서 정의된 타원곡선 위의 점들의 덧셈은 실수체에서 정의된 타원곡선 상의 점들의 덧셈과 정의가 거의 동일합니다. 다만, 실제 좌표값을 계산할 때 $\mod {p}$ 에 대해 계산해야 합니다.

타원곡선 상에서 정의된 군(group)

실수체 상에서 정의된 타원곡선 위의 점들이 abelian group을 이루듯이, 유한체 상에서 정의된 타원곡선 상의 점들은 abelian group을 이루게 됩니다. 타원곡선 상의 점들이 이루는 group의 원소의 개수를 order로 정의하겠습니다.

타원곡선 상의 generator, sub group

유한체 상에서 정의된 타원곡선은 재미있는 성질이 있습니다. 유한체 상에서 임의의 점을 골라, 해당 점을 여러 번 더합니다. 이를 scalar multiplication이라고 합니다.

nP = \underbrace{P + P + ... + P}_{\text{n times}}

타원곡선 상의 점을 scalar multiplication을 해 나가다 보면, 특정 주기로 같은 원소가 반복됨을 알 수 있습니다. 예시를 들어보겠습니다.

다음과 같이 타원곡선 $y^{2} = x^{3} + 2x + 3 \pmod {97}$ 과, 타원곡선 상의 점 $P = (3, 6)$ 가 있다고 할 때, $P$ 에 scalar multiplication을 해 보겠습니다.

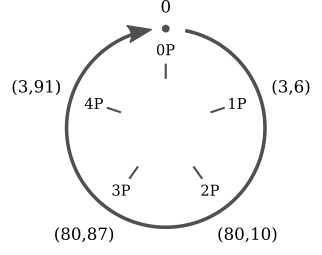
$P$ 를 5번 더하면 무한원점이 됨을 알 수 있습니다. 유한체 상에서 정의된 타원곡선 상의 어떤 점을 골라도 scalar multiplication을 했을 때 유한한 범위 내에서 덧셈의 결과가 반복됨을 알 수 있습니다.
그리고 타원곡선 상의 점에 대해 scalar multiplication을 한 결과들의 집합은 다시 군(group)을 이루게 됩니다. 이는 타원곡선 상의 점들이 이루고 있는 군의 부분군(subgroup)이 됩니다.

점 $P$ 를 generator, 혹은 base point 로 명명합니다. 위의 예시에서는 점 $P$ 가 order 5의 cyclic sub group을 generate함을 알 수 있습니다.

Subgroup의 order가 가지는 성질에 대해 좀 더 살펴보겠습니다.
Subgroup의 order를 $n$ 이라고 하고, 타원곡선 상의 점들이 형성하는 group의 order를 $N$ 이라고 했을 때, Lagrange's Theorem 에 의해 $n$ 은 항상 $N$ 의 약수가 됩니다.

For \;a \;group \;G \;with \;order \;N, \;and \;subgroup \;of \;G \;with \;order \;n \\ \exists \;h \;s.t. \\ N = nh

이 때, $h$ 를 subgroup에 대한 cofactor 라고 명명합니다.

타원곡선 상의 점이 generate하는 subgroup의 order는 어떻게 알 수 있을까요? Subgroup의 order는 항상 $N$ 의 약수이므로, $N$ 의 약수들 중 $nP = 0$ 가 성립하는 가장 작은 $n$ 을 구하면 됩니다.

Order가 $n \;= \;N \;/ \;h$ 인 subgroup을 generate하는 점을 알아내는 것도 어렵지 않습니다. 이 때 $n$ 은 소수라고 가정하겠습니다.
타원곡선 상의 임의의 점 $P$ 에 대해, 항상 $NP = 0$ 을 만족하고, $NP = (nh)P$ 이기 때문에, 점 $hP$ 를 $n$ 만큼 scalar multiplication한 값이 0이 됨을 알 수 있습니다.
Subgroup의 order는 곧, generator에 scalar multiplication을 했을 때 0이 되게 하는 가장 작은 양수값이므로, 점 $hP$ 가 order가 $n$ 인 subgroup을 generate한다는 것을 알 수 있습니다. (단, $hP \not= 0$ )

타원곡선 상에서 정의된 discrete logarithm 문제

타원곡선 상의 discrete logarithm 문제는 바로 order가 $n$ 인 subgroup 상에서 정의됩니다.
Subgroup의 generator $P$ 와, 점 $Q$ 가 주어졌을 때,

Q = kP

를 만족하는 $k$ 를 구하는 것입니다. 이는 앞서 살펴본 ElGamal system의 기초가 된 유한체 상에서 정의된 discrete logarithm 문제와 매우 유사합니다. 하지만 타원곡선 상의 discrete logarithm 문제가, 다른 일반적인 암호 시스템에서 사용되는 discrete logarithm 문제보다 더 어렵다는 것이 알려져 있습니다.

다음 포스트에서는 타원곡선 상의 discrete logarithm 문제를 기반으로 고안된 ECDH, ECDSA에 대해 알아보겠습니다.