<Hard> Edit Distance (LeetCode : C#)

https://leetcode.com/problems/edit-distance/

📕 문제 설명

두 문자열 주어질 때 한 단어를 다른 단어로 변환하는데 필요한 최소한의 연산 수 반환하기

• 연산 종류

1. 삽입
2. 삭제
3. 교체

• Input
  두 단어 word1, word2
• Output
  변환하는데 필요한 최소 연산 수

예제

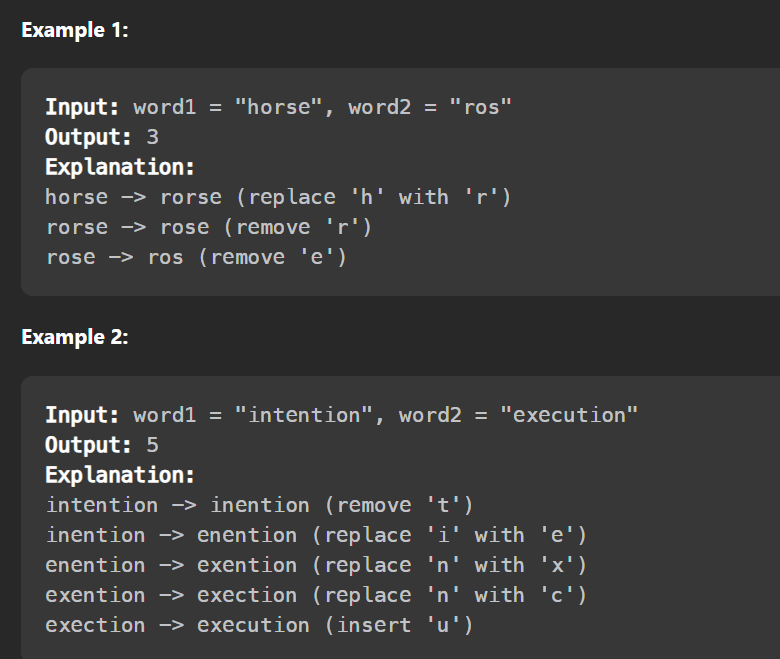
풀이

DP로 유명한 문젠데 점화식 이해하는게 좀 어려웠던 것 같다.

DP[i][j]: i를 사용해 j를 만드는데 필요한 최소 연산 수

1) DP[i-1][j-1] + 0 또는 (같은 경우) + 1 (다른 경우) (replace or not) : i랑 j 다르면 교체해야함
2) DP[i-1][j] + 1 (remove) : j 하나 삭제해야함
3) DP[i][j-1] + 1 (insert) : j가 하나 더들어 와야함

public class Solution {
    public int MinDistance(string word1, string word2) {
        if (word1 == string.Empty) return word2.Length;
        else if (word2 == string.Empty) return word1.Length;
            
        int [,] res = new int[word1.Length + 1, word2.Length + 1];
        res[0, 0] = 0;
        for (int i = 1; i <= word1.Length; i++) // Delete
        {
            res[i, 0] = i;
        }
        
        for (int i = 1; i <= word2.Length; i++) // Insert
        {
            res[0, i] = i;
        }
            
        
        for (int i = 1; i <= word1.Length; i++)
        {
            for (int j = 1; j <= word2.Length; j++)
            {
                res[i, j] = word1[i - 1] == word2[j - 1] ? 
                res[i - 1, j - 1] : Math.Min(res[i - 1, j -1], Math.Min(res[i - 1, j], res[i, j - 1])) + 1;
            }
        }

                
        return res[word1.Length, word2.Length];
    }
}

결과