<Hard> Maximal Rectangle (LeetCode : C#)

https://leetcode.com/problems/maximal-rectangle/

📕 문제 설명

0과 1로 채워진 행렬이 주어질 때 1만을 포함하는 영역 중 가장 큰 영역 반환

• Input
  0과 1로 채워진 행렬
• Output
  1로된 영역 중 가장 큰 영역

예제

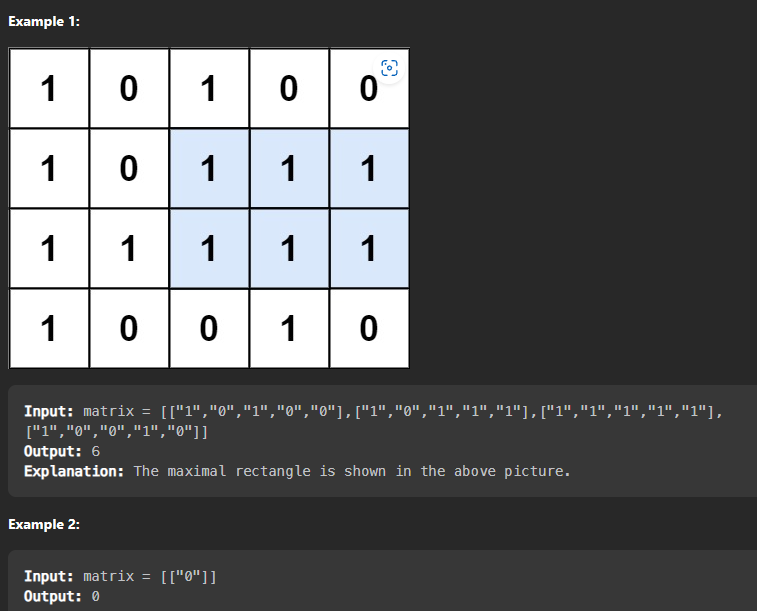
풀이

먼저 떠오른건 brute force 방식으로 보는건데 시간 복잡도가 너무 안 좋을 것 같아서 다른 방식으로 풀게 되었다.

앞에 84번 문제 연장선으로 생각하고 풀 수 있다. 현재 2차원인데 1의 개수를 높이로 생각해서 각 행 기준 연속된 1을 높이로 해서 배열에 값을 저장하여 1차원으로 줄인다. 이후 84번 문제 그대로 사용하면 된다.

ex)
예제로 주어진 것을 다음과 같은 형태로 변경하고 행마다 histogram 높이 구하는 것을 적용해주면 된다.
[4, 0, 3, 0, 0]

[3, 0, 2, 3, 2]

[2, 1, 1, 2, 1]

[1, 0, 0, 1, 0]

public class Solution {
    public int MaximalRectangle(char[][] matrix) {
        int[] heights = new int[matrix[0].Length];

        for (int i = 0; i < matrix[0].Length; i++)
        {
            int height = 0;
            for (int j = 0; j < matrix.Length ; j++)
            {
                if (matrix[j][i] == '1') height++;
            }

            heights[i] = height;
        }

        return LargestRectangleArea(heights);
        
    }

    public int LargestRectangleArea(int[] heights) {
        int n = heights.Length, max = 0;
        var stack = new Stack<int>();
        for(int i = 0; i <= n; i++)
        {
            var height = i < n ? heights[i] : 0;
            // 현재거 기준보다 앞에 큰거 있는 경우 
            while(stack.Count != 0 && heights[stack.Peek()] > height) 
            {
                var currHeight = heights[stack.Pop()];
                var prevIndex = stack.Count == 0 ? -1 : stack.Peek();
                max = Math.Max(max, currHeight * (i - 1 - prevIndex));
            }
            stack.Push(i);
        }
        
        return max;
    }
}

결과