<Hard> Self Crossing (LeetCode : C#)

https://leetcode.com/problems/self-crossing/

📕 문제 설명

distance 정보가 주어진다. 2차원 평면에서 (0, 0)에서 출발할 때 distance에서 한 번 움직일 때 마다 방향을 동서남북으로 변환한다. 경로가 재방문 되는지 여부 반환하기

• Input
  distance 정보
• Output
  self-crossing 여부

예제

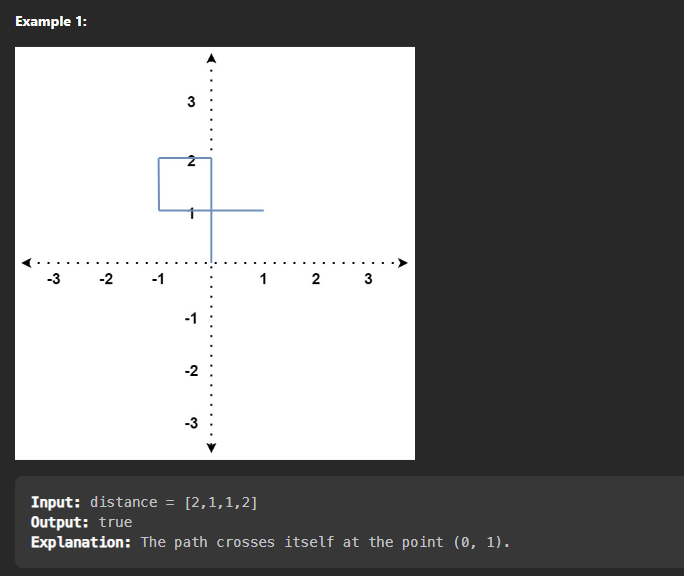
풀이

수학적 규칙으로 풀리는 문제다.
=> 참고 https://www.youtube.com/watch?v=ajFikcnQV1I&t=550s

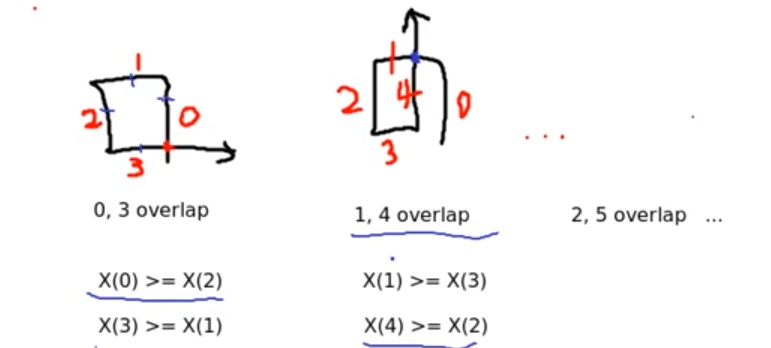
1번 규칙

편의상 4개의 점을 a, b, c, d라고 하면

다음 조건을 만족하는 경우 a와 d가 만나게 된다.
1. a의 x좌표 >= c의 x좌표
2. d의 x좌표 >= b의 x좌표

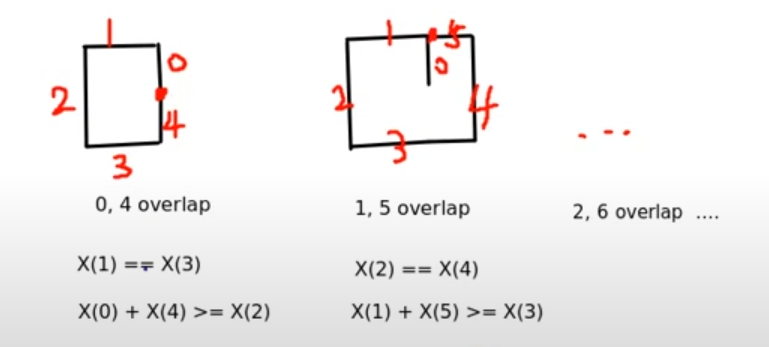
2번 규칙

편의상 5개의 점을 a, b, c, d, e라고 하면

다음 조건을 만족하는 경우 a와 e가 만나게 된다.
1. b와 d의 좌표가 같고
2. a의 x좌표 + e의 x좌표 >= c의 x 좌표

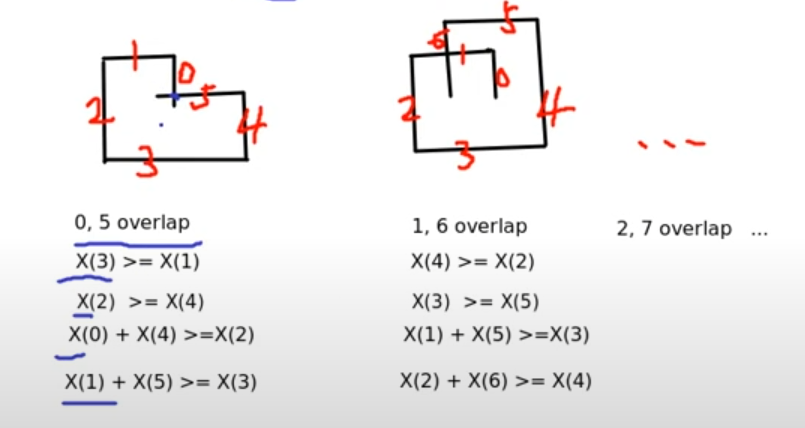
3번 규칙

편의상 6개의 점을 a, b, c, d, e, f라고 하면

다음 조건을 만족하는 경우 a와 f가 만나게 된다.
1. d의 x좌표 >= b의 x좌표
2. c의 x좌표 >= e의 x좌표
3. a의 x좌표 + e의 x좌표 >= c의 x좌표
4. b의 x좌표 + f의 x좌표 >= d의 x좌표

public class Solution {
    public bool IsSelfCrossing(int[] distance) {
        if (distance.Length <= 3) return false;
        
        for (int i = 3; i < distance.Length; ++i) 
        {
            if (distance[i - 2] <= distance[i] && distance[i - 1] <= distance[i - 3]) return true;
            if (i >= 4 && distance[i - 1] == distance[i - 3] && distance[i - 2] <= distance[i] + distance[i - 4]) return true;
                
            if (i >= 5 && distance[i - 4] <= distance[i - 2] && distance[i - 2] <= distance[i] + distance[i - 4] && distance[i - 1] <= distance[i - 3] &&
                distance[i - 3] <= distance[i - 1] + distance[i - 5])
                return true;
        }

        return false;

        
        
    }
}

결과