<Lv.3> 미로 탈출 명령어 (프로그래머스 : C#)

https://school.programmers.co.kr/learn/courses/30/lessons/150365

📕 문제 설명

미로의 (x,y)에서 출발해 (r,c)로 이동하여 탈출해야 한다.

미로 탈출 조건
1. 격자 바깥 나가기 x
2. 출발지점 ~ 도착지점까지 이동거리 = k (같은 격자 2번 이상 방문 ok)
3. 미로에서 탈출한 경로 문자열 중 사전 순으로 가장 빠른 경로로 탈출해야함

이동 경로

l: 왼쪽
r: 오른쪽
u: 위쪽
d: 아래쪽

• Input
  격자의 크기, 출발 위치, 탈출 지점, 탈출까지 이동해야하는 거리
• Output
  미로 탈출 경로 (미로 탈출 불가능시 impossible 반환)

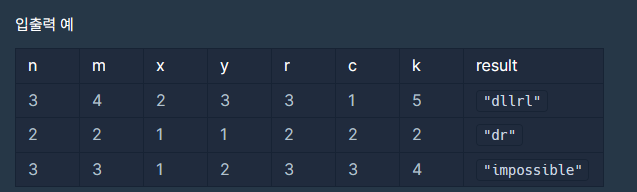
예제

풀이

DFS + 백트래킹으로 이동 거리 k가 될 수 있는지 확인 (사전순 방향을 먼저 봐서 k를 만나면 바로 answer)

using System;
using System.Text;

public class Solution {
    public int[] dx = {1, 0, 0, -1};
    public int[] dy = {0, -1, 1, 0};
    public char[] dir = {'d', 'l', 'r', 'u'};
    public int m;
    public int n;
    public StringBuilder sb;
    public int targetX;
    public int targetY;
    public string answer;
    
    public string solution(int n, int m, int x, int y, int r, int c, int k) {
        this.m = m;
        this.n = n;
        targetX = r;
        targetY = c;        
        sb = new StringBuilder();
        answer = "";
        
        int length = GetDist(x, y, r, c);
        // k, 도착지점까지 거리 짝, 홀 일치 하지 않으면 impossible
        // 이동 가능한 거리가 도착지점보다 짧으면 impossible
        if((k - length) % 2 == 1 || k < length) return "impossible";
        
        DFS(x, y, 0, k);
        return answer == "" ? "impossible" : answer;
    }
    
    // 현재 위치 (x, y) ~ 도착지점까지 거리
    private int GetDist(int x, int y, int r, int c)
    {
        return (int)Math.Abs(x-r) + (int)Math.Abs(y-c);
    }
    
    public void DFS(int x, int y, int movedDist, int k)
    {
        if(answer != "") return;
        // 이동해야할 거리가 k보다 더 긴 경우
        if(movedDist + GetDist(x, y, targetX, targetY) > k) return;
        if(k == movedDist) // 이동 거리가 k가 되면 answer
        {
            answer = sb.ToString();
            return;
        }
        
        for(int i = 0; i < 4; i++)
        {
            int newX = x + dx[i];
            int newY = y + dy[i];
            if (newX <= 0 || newY <= 0 || newX > n || newY > m) continue;
            
            // DFS + back tracking
            sb.Append(dir[i]);
            DFS(newX, newY, movedDist + 1, k);
            sb.Remove(movedDist, 1);
        }
    }
}

결과