<Lv.3> 억억단을 외우자 (프로그래머스 : C#)

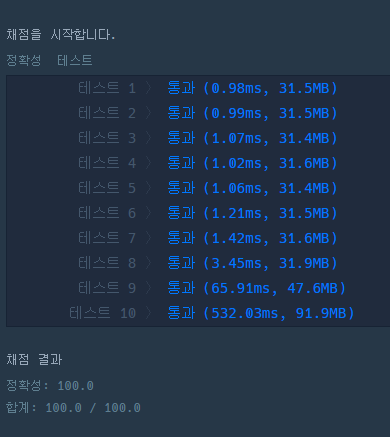
https://school.programmers.co.kr/learn/courses/30/lessons/138475

📕 문제 설명

적당한 수 e를 먼저 알려주고, e 이하의 임의의 수 s가 여러개 주어진다. 각 s에 대해 s보다 크거나 같고 e보다 작거나 같은 수 중에서 억억단에서 가장 많이 등장한 수를 답해야 한다. (여러개라면 그 중 가장 작은 수)

억억단은 1억x1억 크기의 행렬, matrix[i][j] = i x j

• Input
  e와 s의 목록
• Output
  각 퀴즈의 답 목록

예제

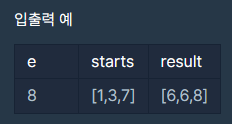
풀이

결국 억억단에 등장한 횟수는 해당 숫자의 약수의 개수로 볼 수 있다. (약수의 곱으로 만들어지며, matching되는 수는 어차피 약수에도 각자 1번씩 등장하므로 자연스레 개수가 세짐)
ex) 16 = 1, 2, 4, 8, 16
(1x16, 2x8, 4x4, 8x2, 16x1) => 5개

e에서부터 거꾸로 보면서 dp[i]를 갱신한다.
dp[i] = i ~ e까지 중 억억단에 등장한 횟수가 가장 많은 수

+) 약수 개수를 얼마나 빨리 구할 수 있냐에 따라 10번 테케 시간 초과 여부가 갈린다..!

using System;
using System.Linq;

public class Solution {
    public int[] solution(int e, int[] starts) {
        int[] answer = new int[starts.Length];
        
        int[] divisorCount = new int[e+1];
        
        for(int i = 2 ; i <=e ; i++)
        {
            for(int j = 1 ; j <=(e/i) ; j++)
            {
                divisorCount[i*j]++;
            }
        }
        int minStart = starts.Min();
        
        int[,] dp = new int[e+1, 2];
        dp[e,0] = divisorCount[e];
        dp[e,1] = e;
        // dp[i] = i~e 중 가장 개수 많은 것
        for (int i = e - 1; i >= minStart; i--)
        {
            // i가 여태까지 억억단 중복 개수 중 가장 많다면 갱신 or 개수 같고 숫자 더 작으면 갱신
            if (divisorCount[i] >= dp[i+1, 0])
            {
                dp[i, 0] = divisorCount[i];
                dp[i, 1] = i;
            }
            else
            {
                dp[i, 0] = dp[i+1, 0];
                dp[i, 1] = dp[i+1, 1];
            }
        }
        
        for (int i = 0; i < starts.Length; i++)
        {
            int start = starts[i]; // 이 범위 부터 e 범위 까지 중 가장 큰 것의 index 필요
            answer[i] = dp[starts[i], 1];
        }
        
        return answer;
    }
}

결과