<Lv.4> 쌍둥이 빌딩 숲 (프로그래머스 : C#)

https://school.programmers.co.kr/learn/courses/30/lessons/140105

📕 문제 설명

높이가 1~n까지 각각 2채씩 총 2n채의 빌딩이 존재한다. 이때, 같은 높이를 가지는 빌딩 사이에는 그보다 높은 빌딩이 존재하지 않는다.

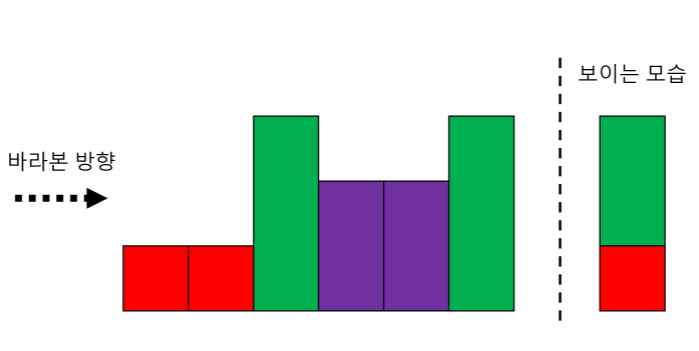
한쪽 측면에서 빌딩 숲을 바라보면 count채의 빌딩이 구분되어 보인다. 다른 빌딩에 의해 전체가 가려지지 않는다면 서로 다른 높이의 빌딩을 볼 수 있다. 빌딩들이 배치될 수 있는 방법의 수 반환하기

• Input
  n, count
• Output
  빌딩들이 배치될 수 있는 방법의 수

예제

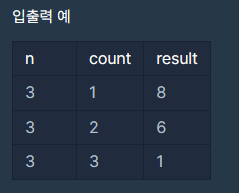
풀이

dp[i, j] = 쌍둥이 건물 i쌍에 count j를 가지는 경우

어느 위치에 작은 건물들을 끼워 넣을 것인지를 기준으로 점화식을 세운다.
(높은 빌딩 사이 더 높은 빌딩이 위치할 수 없으므로, 이전 dp 상태에서 아무 곳에나 끼워 넣을 수 있는 작은 건물을 기준으로 생각하는 것이 편함)

dp[i,j]는 다음의 두 영향을 받는다.

1) (i-1, j)인 곳에서 가장 낮은 건물을 중간에 끼워 넣는 경우 (맨 앞에 놓지 X)
=> dp[i-1, j] x (i-1) x 2 (이전 빌딩의 총 개수 = 2 x (쌍둥이 빌딩 쌍의 개수 - 1))

2) (i-1, j-1)인 곳에서 가장 낮은 건물을 맨 앞에 놓는 경우
=> 1(맨 앞에 놓는 경우의 수) x dp[i-1, j-1]
=> 제일 낮은 건물 앞에 두면 count가 1 증가한다. i-1 => 건물 쌍 추가하게 되면 i가 되고, j-1도 count추가되면서 j가 되므로 해당 점화식이 세워진다.

+) answer이랑 dp를 long으로 정의하지 않으면 테케 통과가 되지 않는다.

using System;

public class Solution {
    public int solution(int n, int count) {
        long answer = 0;
        long[,] dp = new long[n+1,n+1]; // dp[n, count]
        dp[1,1] = 1;
        
        for(int i= 2; i <= n; i++)
        {          
            for(int j = 1; j <= i; j++)
            {              
                dp[i,j] = (dp[i-1,j] * (i-1) * 2 + dp[i-1,j-1]) % 1000000007;
            }
        }
        
        answer = dp[n, count];
        
        return (int)answer;
    }
}

결과