<Medium> Sum of Subarray Minimums (LeetCode : C#)

https://leetcode.com/problems/sum-of-subarray-minimums/

📕 문제 설명

정수 배열이 주어질 때 모든 하위 배열들의 최솟값들의 합 반환하기
(modulo 10^9 + 7 적용해서 반환)

• Input
  정수 배열
• Output
  모든 하위 배열들의 최솟값들의 합

예제

시도 1.

현재의 최솟값은 이전의 최솟값들 중 최소를 가져오는 식으로 구성된다.
[3, 1, 2, 4]

1) [3, 1]
2) [1, 2]
3) [2, 4]

1)은 3과 1 중 최소, 2)는 1과 2중 최소, 3)은 2와 4중 최소를 가져오게 되고 뒤에 더 긴 길이로 볼때도 이 과정은 동일하게 적용된다.

결국 index적으로 보면 이전 결과들에 대해 i, i+1 중 최소를 가져오면 되는 식이다. (그래서 2차원 dp로 진행))

dp[i, j] = i개수로 볼 때 j번째에 해당되는 묶음의 최솟값

public class Solution {
    public int SumSubarrayMins(int[] arr) {
        long answer = 0;
        int n = arr.Length;
        int[,] dp = new int[n, n];

        for (int i = 0; i < n; i++)
        {
            dp[0,i] = arr[i];
            answer += dp[0,i];
        }

        for (int i = 1; i < n; i++)
        {
            for (int j = 0; j < n - i; j++)
            {
                dp[i, j] = Math.Min(dp[i - 1, j], dp[i - 1, j + 1]);
                answer += dp[i, j];
            }
        }

        return (int) (answer % 1000000007);  
    }
}

풀이

monotonic stack 이용한 풀이

• monotonic stack: 모든 원소들이 오름차순 또는 내림차순을 유지하도록 하여 바로 다음 큰값이나, 바로 다음 작은 값을 구해야할 때 사용할 수 있는 stack

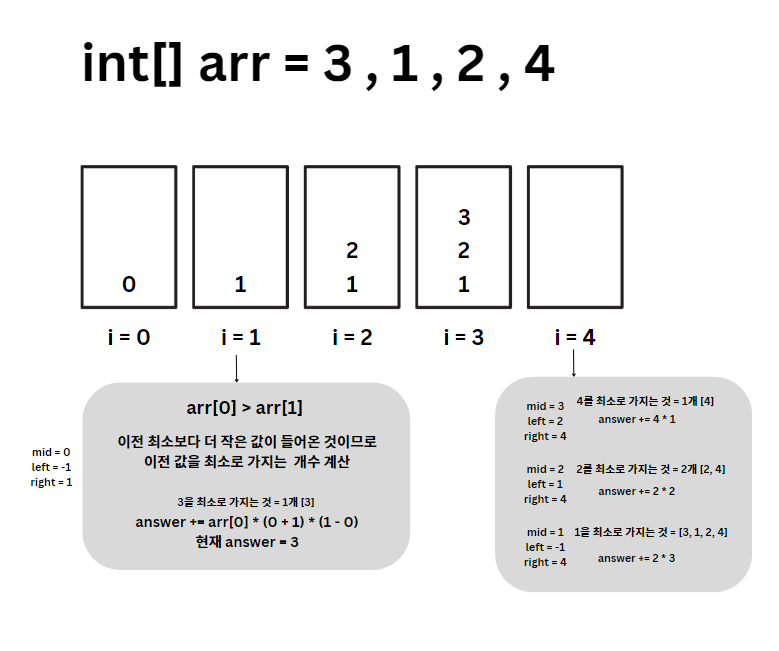
[3, 1, 2, 4]
예제 기준 3을 최소로 가지는 구간은 [3], 1을 최소로 가지는 구간은 [3, 1, 2, 4], 2를 최소로 가지는 구간은 [2, 4], 4를 최소로 가지는 구간은 [4]이다.

[left, n index (mid), right]면 n이 최솟값이 되는 하위 배열의 수는 (n의 index - 왼쪽 boundary) * (오른쪽 boundary - n의 index) 이다.
=> 왼쪽과 오른쪽으로 쪼갠 후 조합을 구해나가기 때문에 곱하기로 계산한다.

따라서, monotonic stack을 기반으로 현재 값을 최소로 가지는 왼쪽과 오른쪽 boundary를 구한다. 여기서 stack은 모든 원소들이 오름차순 그리고 n을 최솟값으로 가지는 수 만큼 곱해서 answer에 더해나가면 전체 하위 배열들에 대한 최소의 합을 구할 수 있다.

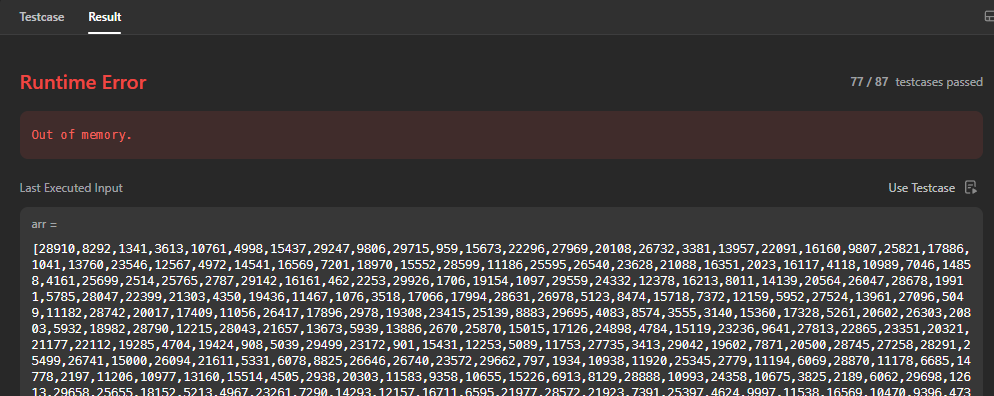
public class Solution {
    public int SumSubarrayMins(int[] arr) {
        if (arr == null || arr.Length == 0) return 0;

        long answer = 0;
        Stack<int> stack = new Stack<int>();

        for(int i = 0; i <= arr.Length; i++)
        {
        	// 들어온 애가 더 최소이므로 지금의 최소는 개수 세서 answer에 더하기
            while(stack.Count > 0 && arr[stack.Peek()] > (i == arr.Length ? -1 : arr[i])) 
            {
                int mid = stack.Pop();
                int left = stack.Count == 0 ? -1 : stack.Peek();
                int right = i;

                answer += (long)(arr[mid]) * (mid - left) * (right - mid);
            }
            stack.Push(i);
        }
        return (int)(answer % 1000000007);
    }
}

결과