🔑 해싱이란?
키에 산술적인 연산을 적용하여 항목이 저장되어 있는 테이블의 주소를 계산하여 항목에 접근한다.
이렇게 키에 대한 연산에 의해 직접 접근이 가능한 구조를 해시 테이블이라 부르며, 해시 테이블을 이용한 탐색을 해싱이라 한다.
현상
- 충돌
서로 다른 키를 갖는 항목들이 같은 해시주소를 가지는 현상이다.- 오버플로우
충돌이 발생하고, 해시 주소에 더이상 빈 버킷이 남아 있지 않으면 발생한다. 오버플로우가 발생하면 해시테이블에 항목을 더 이상 저장하는 것이 불가능해진다.
해싱방법
선형조사법
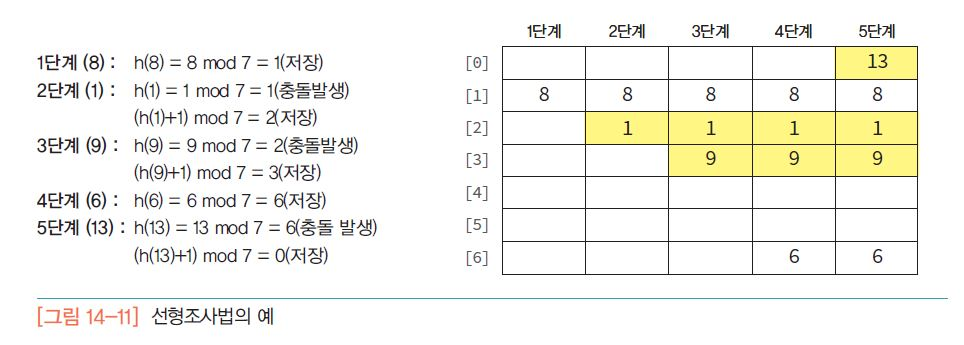
만약 충돌이 ht[k]에서 발생했다면 ht[k+1]이 비어 있는지를 살펴본다.
만약 비어있지 않다면 ht[k+2]를 살펴본다. 이런 식으로 비어있는 공간이 나올 때까지 계속하여 조사하는 방법이다.
만약 테이블의 끝에 도달하게 되면 다시 테이블의 처음으로 간다.
만약 조사를 시작했던 곳으로 되돌아오게 되면 테이블이 가득 찬 것으로 판단한다.
문제점
클러스터링문제: 저장된 숫자들이 모여있을때 탐색횟수가 늘어나게되는 문제
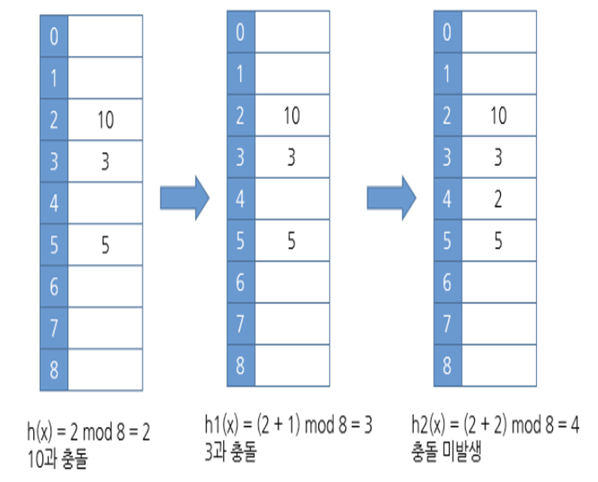
이차조사법
이차조사법에서는 만약 충돌이 ht[k]에서 발생했다면 ht[k+1]이 비어 있는지를 살펴본다. 만약 비어있지 않다면 ht[k+4]를 살펴본다.
이런 식으로 비어있는 공간이 나올 때까지 k+n제곱으로 계속하여 조사하는 방법이다.
만약 테이블의 끝에 도달하게 되면 다시 테이블의 처음으로 간다.
만약 조사를 시작했던 곳으로 되돌아오게 되면 테이블이 가득 찬 것으로 판단한다.
문제점
클러스터링문제: 2차 클러스터링 문제 -> 집중되어지는 slot을 중심으로 클러스터링이 발생될 확률이 여전히 높다
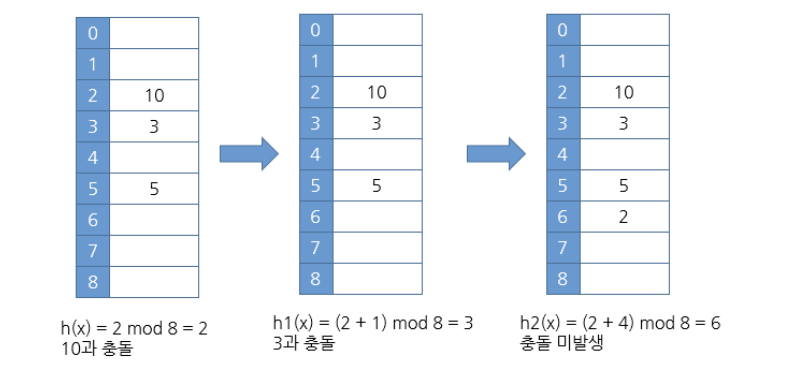
이중해싱법
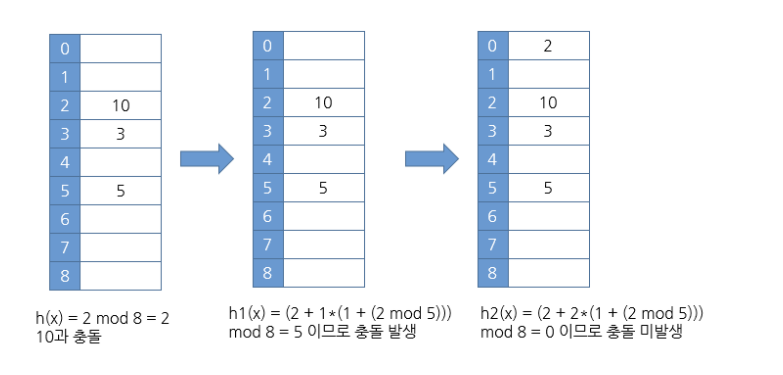
이중해싱법에서는 만약 충돌이 ht(k)에서 발생했다면 (h(k)+1*h'(k))이 비어 있는지를 살펴본다.
만약 비어있지 않다면 (h(k)+2*h'(k))를 살펴본다.
이런 식으로 비어있는 공간이 나올 때까지 계속하여 조사하는 방법이다.
만약 테이블의 끝에 도달하게 되면 다시 테이블의 처음으로 간다.
만약 조사를 시작했던 곳으로 되돌아오게 되면 테이블이 가득 찬 것으로 판단한다.
체인법
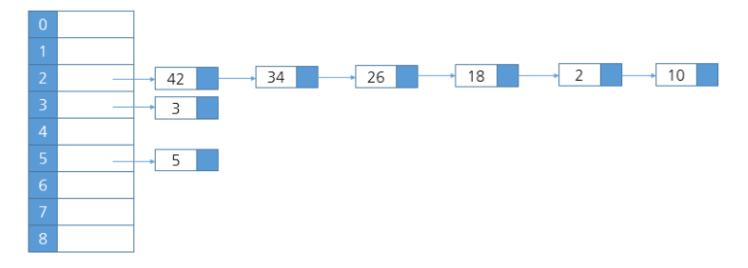
충돌을 해결하는 두 번째 방법은 해시 테이블의 구조를 변경하여 각 버킷이 하나 이상의 값을 저장할 수 있도록 하는 것이다.
즉, 각 버킷에 고정된 슬롯을 할당하는 것이 아니라 각 버킷에 삽입과 삭제가 용이한 연결 리스트를 할당한다.
물론 버킷 내에서는 원하는 항목을 찾을 때는 연결 리스트를 순차 탐색한다.
문제점
링크 공간의 필드가 필요하다