from previous blog..
코딩을 덮어씌운 수학문제이다.
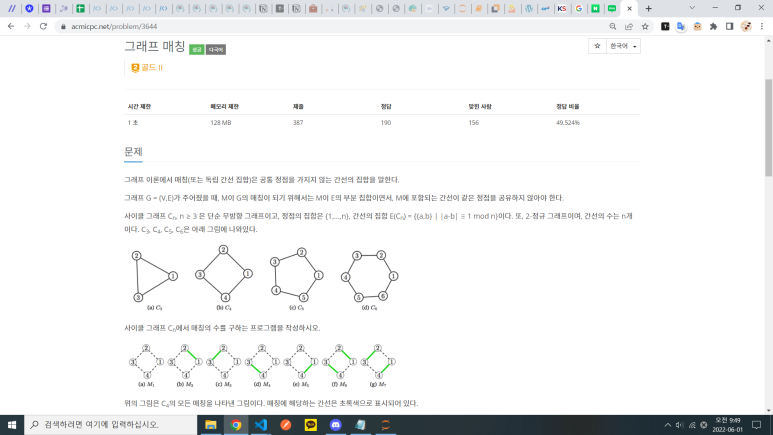
이 문제를 풀기 위해 우리는 임의의 Cn을 생각해볼 필요가 있다. 이 때 Cn 의 matching의 갯수를 Mn , 그리고 Cn위의 임의의 한 간선 e를 생각해보자. 우선 결론부터 말하자면, e를 포함하지 않고, e와 인접한 두 간선을 동시에 포함하지 않은 모든 matching의 갯수 = Mn-1이 되고, 나머지의 갯수는 Mn-2이 된다.
(그림 참고) 이를 쉽게 이해하기 위해 간단히 n=5라는 예시를 들어본다.
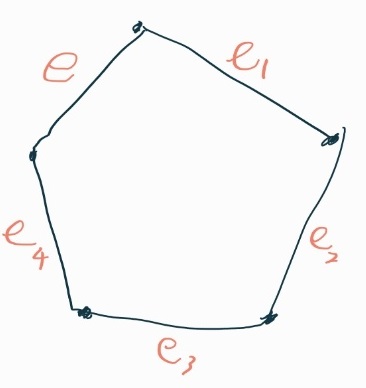
아래 그림에서 e를 포함한 matching은, e1과 e4를 둘 다 포함할 수 없으므로, e를 제외하면 {}, {e2}, {e3}이 될 수 있고, 갯수는 총 3개이다.
그리고 e를 포함하지 않은 matching은, e1과 e4를 동시에 포함할 수 있으므로 {e1,e4}, {}, {e1}, {e2}, {e3}, {e4}, {e1,e3}, {e2,e4}이 될 수 있고, 마찬가지로 갯수는 총 8개이다.
처음으로 살펴볼 것은 e를 포함하지 않는 matching중 e와 정점을 공유하지 않는 두 간선을 모두 포함하지 않는 matching이다. (여기서는 {e1,e4}가 유일한 예외 케이스이다.) 결과적으로 이것은 e1 ~e4를 간선으로 가지는 C4의 모든 matching과 완전히 동일한 결과가 나온다.(세세한 계산은 생략한다.) 따라서 그 합은 M4가 된다.
나머지를 살펴보자. 이 경우는 약간의 생각의 전환이 필요한데 이런저런 과정은 무시하고 간단히 2가지 케이스로 설명을 할 예정이다.
우선 e,e1,e4를 한개의 간선 e5라 생각하자. matching의 관점과 위의 나머지 케이스에서 e5가 선택되는 케이스는 e1과 e4가 선택된 케이스(즉, e가 선택되지 않은 케이스)이고, e5가 선택되지 않는 케이스는 e가 선택된 케이스(즉, e1과 e4가 둘다 선택되지 않은 케이스)가 된다.
따라서 그 합은 역시 M3이 된다.
위의 두 과정에서 우리는 C5의 matching과 C3의 matching union C4의 matching 이 1:1 대응임을 보였다.
그리고 마지막으로, 이를 일반화할 경우 다음과같은 식이 나올 수 있다.
M5 = M4 + M3 , Mn = Mn-1 + Mn-2
