---

[4주차]

TIL

고전제어 강의 소개

• 자율주행 시스템 아키텍처

• 상태공간 방정식

신호처리: Filter

• Average filter

• Moving average filter

• Low pass filter

• State observers

• Kalman filter

PID 제어

---

4주차 skill set

1) Modeling 2) Filter 3) PID control

---

학습내용

[1] 고전제어 강의 소개 (Intro.)

1. 자율주행 시스템 아키텍처

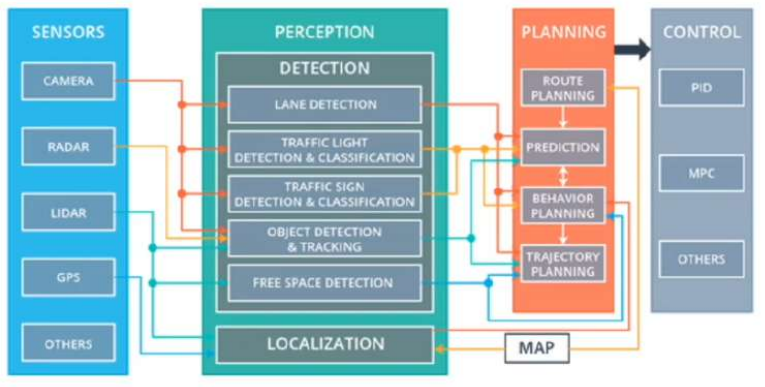
• 자율주행 시스템 순서
  Input dst
  --> Rout planning
  --> Perception (Sensor -> Localization&Map + Detection)
  --> Planning (Prediction -> Behavior Planning -> Trajectory Planning)
  --> Control

2. 학습목표

• 이번 Planning & Control 강의에서는 prediction -> trajectory -> control 에 중점을 두고 공부한다.

• 학습 순서: 제어하는 법 (control) -> 경로계획 방법 (trajectory) -> 주변 사물의 거동예측을 통한 판단 (prediction)

• 항상 이번 학습을 통해 얻을 skill set 이 무엇인지 생각하고 정리하자.

[2] 상태공간 방정식 (State-space equation)

1. Coordinate system

• World coordinate
• Vehicle coordinate

2. Modeling

• Translational system: ΣF=Ma
• Rotational system: ΣT=Iα
• D'Alembert's principle

3. State-space equation

• State variable: 시스템의 거동을 결정하는 최소 개수의 변수
• State vector: 상태 변수들의 집합 (n개의 변수)
• State space: 상태 벡터들의 집합 (n차원 공간)

• 동적 시스템의 상태, 입/출력을 벡터 형태로 표현하고, 시스템의 동작을 시간에 대한 함수로 모델링한다.

• 상태공간이 필요한 이유: 동적 시스템을 효율적인 선형 방정식으로 다룰 수 있다.

• 간단한 예시
  

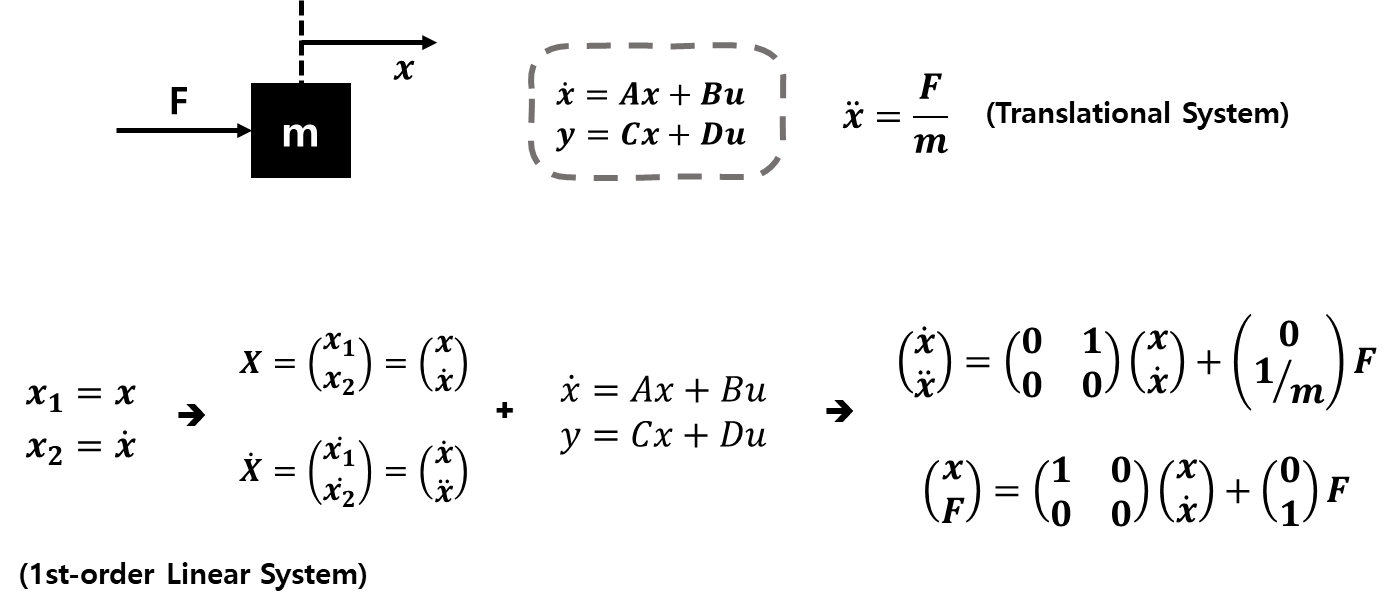
[3] 신호처리: Filter

1. Average Filter (평균필터)

• 가장 간단한 형태의 재귀(Recursive)필터

  • 재귀필터: 과거 추정치와 측정값으로 현재 추정치를 계산

• 측정된 모든 데이터의 평균을 추정값으로 사용한다.

  • 단점: 과거 데이터가 많아질수록 최근 데이터의 양상이 반영되기 힘들다.

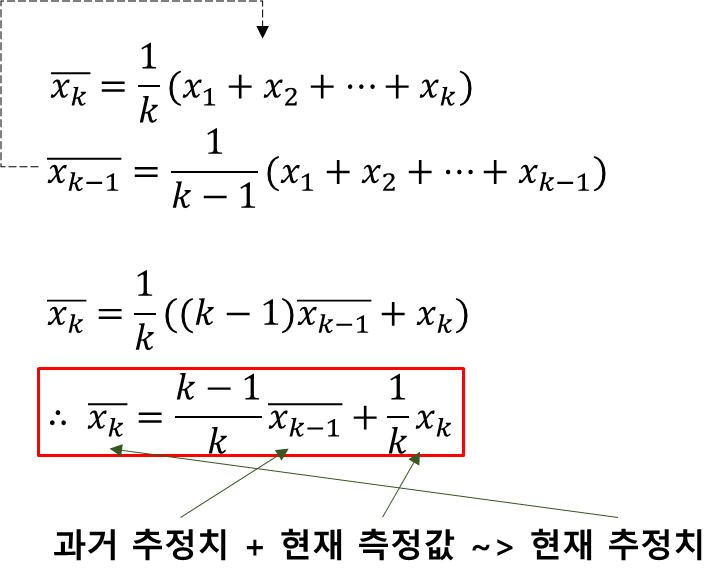
• Ex01) AverageFilter.py

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 필터 클래스 생성
class AverageFilter:
    # 클래스 초기화
    def __init__(self, y_initial_measure):
        # 추정치 초기값 = 측정치 초기값
        self.y_estimate = y_initial_measure
        # 계산할 측정값의 개수
        self.k = 1
        
    # *** 실제 평균필터 방정식을 적용시키는 함수 ***
    def estimate(self, y_measure):
        # 측정치 (csv 파일에서 받아올 값)
        self.y_measure = y_measure
        # Q)메서드 내에서 계산할 때 멤버 앞에는 무조건 self. 를 붙여야 하는건가...?
        # A)self. 는 인스턴스를 나타내는 것이다. 메서드 내에서 self.를 사용해야 인스턴스 변수에 접근할 수 있기 때문에 꼭 써야한다.
        self.y_estimate = (self.k-1) * self.y_estimate / self.k + self.y_measure / self.k
        self.k += 1


# if __name__ == "__main__": 이게 스크립트 파일을 구분하기 위한 표시라고 한다.
# 현재 모듈에서 직접 실행 시켜야만 작동하는 블록(?)이다. 다른 모듈에서 import 해서 사용할 때 작동하지 않는 부분이다.
if __name__ == "__main__":
    # pandas 라이브러리의 scv를 읽는 함수를 사용하여 signal에 2차원 dataFrame 형식으로 데이터를 저장한다. (Matrix)
    signal = pd.read_csv("Data/example_Filter_1.csv")
    # 실행 전에 y_estimate 열의 성분들을 0으로 초기화 시켜주는 작업이다. (없어도 되는데 공부삼아 넣었다.)
    signal['y_estimate'] = np.zeros(len(signal))

    # y_estimate이라는 인스턴스 생성 (초기 x0 저장됨)
    y_estimate = AverageFilter(signal.y_measure[0])

    # 행, 열 수 만큼 반복 (y_estimate의 계산값을 update한다.)
    for i, row in signal.iterrows():
        # MovingAverageFilter 클래스의 estimate 메소드를 사용하여 signal의 y_measure행 i열의 값으로 y_estimate를 계산한다.
        y_estimate.estimate(signal.y_measure[i])
        # 위에서 계산된 y_estimate를 새로운 행 i에 update 한다.
        signal.y_estimate[i] = y_estimate.y_estimate

    # 모두 계산 된 siganal의 dataFrame을 한번 살펴본다.
    print(signal)

    # MatLAB Plot과 매우 유사하다. (아마 거기서 가져온 거 아닐까 하는 생각..?)
    # figure 제목
    plt.figure('ex01_AverageFilter')
    # 플롯팅 할 (x좌표, y좌표, 선종류, 데이터 명)을 입력한다.
    plt.plot(signal.time, signal.y_measure,'k.',label = "Measure")
    plt.plot(signal.time, signal.y_estimate,'r-',label = "Estimate")
    # x, y 좌표계 이름을 설정한다.
    plt.xlabel('time (s)')
    plt.ylabel('signal')
    # legend(범례)가 그래프 상 최적의 위치에 배치되도록 자동으로 설정하라는 의미이다.
    plt.legend(loc="best")
    # x, y축의 크기를 동일하게 설정하라는 의미이다.
    plt.axis("equal")
    # grid on
    plt.grid(True)
    plt.show()

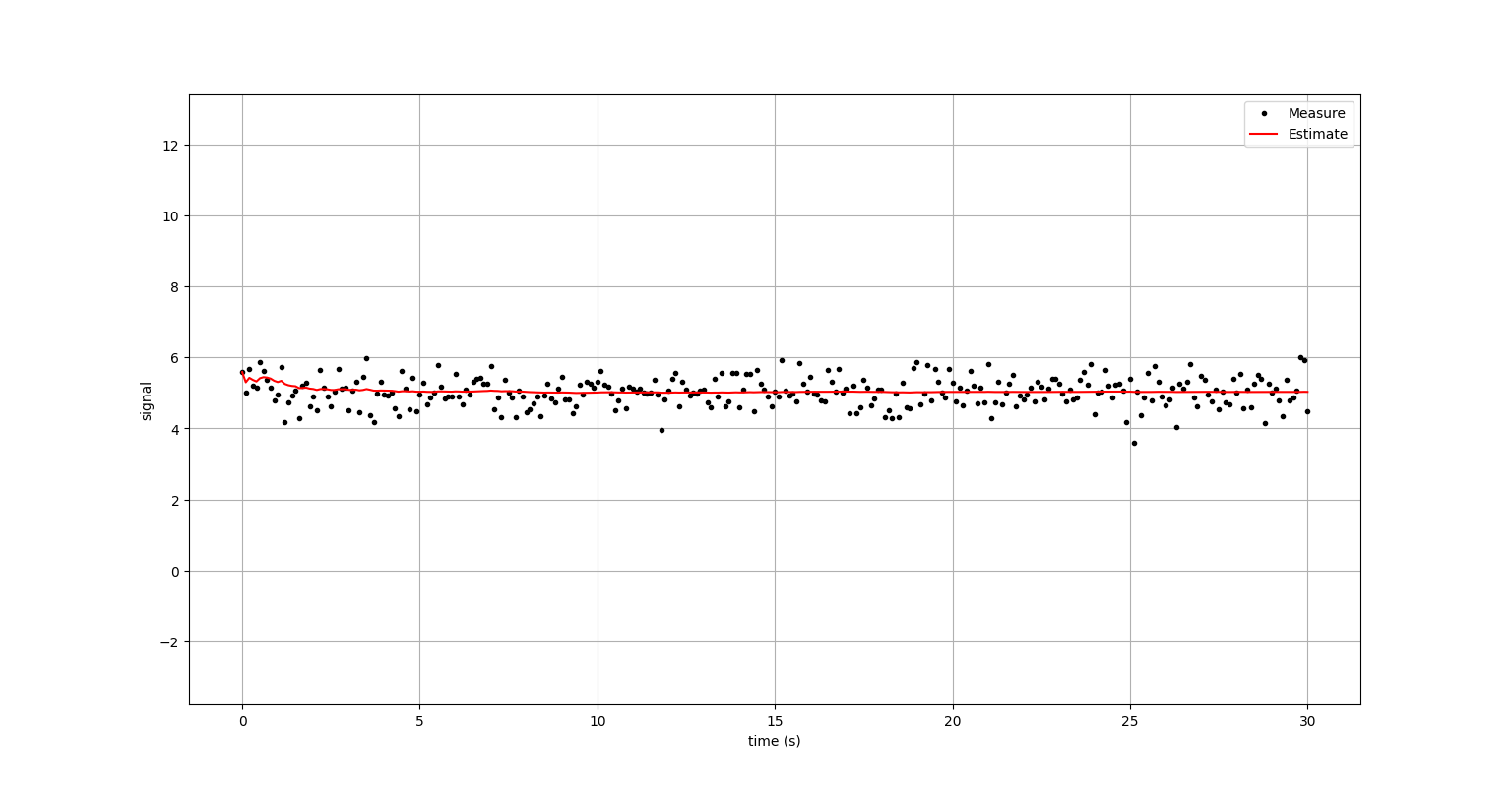
2. Moving Average Filter (이동평균필터)

• 평균필터의 단점을 보완하고자, 시스템의 동적인 변화를 반영한 필터

• 평균을 계산할 데이터의 구간을 정해서 과거 데이터를 어느정도 무시

  • 단점: 여전히 '평균'이므로 모든 데이터의 가중치가 동일하다는 한계가 있다.

• Ex02) MovingAverageFilter.py

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Buffer열할을 할 큐(queue)를 만들기 위해 가져온 라이브러리이다.
import queue

# 이동평균필터 클래스
class MovingAverageFilter:
    # 클래스를 초기화 해주는데, 평균계산할 데이터의 개수 n을 여기서 바로 지정한다.
    def __init__(self, y_initial_measure, n=10):
        # y_Buffer라는 이름의 queue를 만들었다. (FIFO 방식으로 데이터를 저장한다!!!)
        # FIFO 방식의 데이터 처리를 도와주는 queue는 나중에 오래된 센서 데이터를 처리할 때 사용될 수 있을 것 같다.
        self.y_Buffer = queue.Queue()
        # Buffer 초기화 작업 (n개의 데이터를 저장하는 buffer의 모든 데이터를 초기 측정값으로 채움, 필터링 전 일종의 보정을 하는 것)
        for _ in range(n):
            self.y_Buffer.put(y_initial_measure)
        # 마찬가지로 인스턴스 변수에 접근하기 위해 self. 를 붙여 멤버를 선언해 준다.
        self.n = n
        self.y_estimate = y_initial_measure

    # y_estimate를 구하는 실제 이동평균필터 방정식을 적용시키는 함수
    def estimate(self, y_measure):
        # 인스턴스 접근을 위한 멤버 선언
        self.y_measure = y_measure
        # 해당 시점의 Buffer에 가장 먼저 추가되었던 y_measure 값을 제거함과 동시에 반환하여 y_previous_measure에 할당한다.
        self.y_previous_measure = self.y_Buffer.get()
        # FIFO 방식의 데이터 처리로 인해 한 자리가 남는다. 그 자리에 새로운 y_measure 값을 넣어준다.
        self.y_Buffer.put(y_measure)
        # *** 고로 여기서 y_previous_measure는 buffer에서 가장 최근에 떨어져 나온, x_(k-u)에 해당하는 측정치이다. ***
        self.y_estimate = self.y_estimate + (self.y_measure - self.y_previous_measure) / self.n
        # 결국 이 메소드의 목적은 추정치 self.y_estimate를 계산하는 것이다.
        return self.y_estimate

if __name__ == "__main__":
    signal = pd.read_csv("Data/example_Filter_2.csv")
    signal['y_estimate'] = np.zeros(len(signal))
    y_estimate = MovingAverageFilter(signal.y_measure[0])

    for i, row in signal.iterrows():
        y_estimate.estimate(signal.y_measure[i])
        signal.y_estimate[i] = y_estimate.y_estimate

    print(signal)

    plt.figure('ex02_MovingAverageFilter')
    plt.plot(signal.time, signal.y_measure,'k.',label = "Measure")
    plt.plot(signal.time, signal.y_estimate,'r-',label = "Estimate")
    plt.xlabel('time (s)')
    plt.ylabel('signal')
    plt.legend(loc="best")
    plt.axis("equal")
    plt.grid(True)
    plt.show()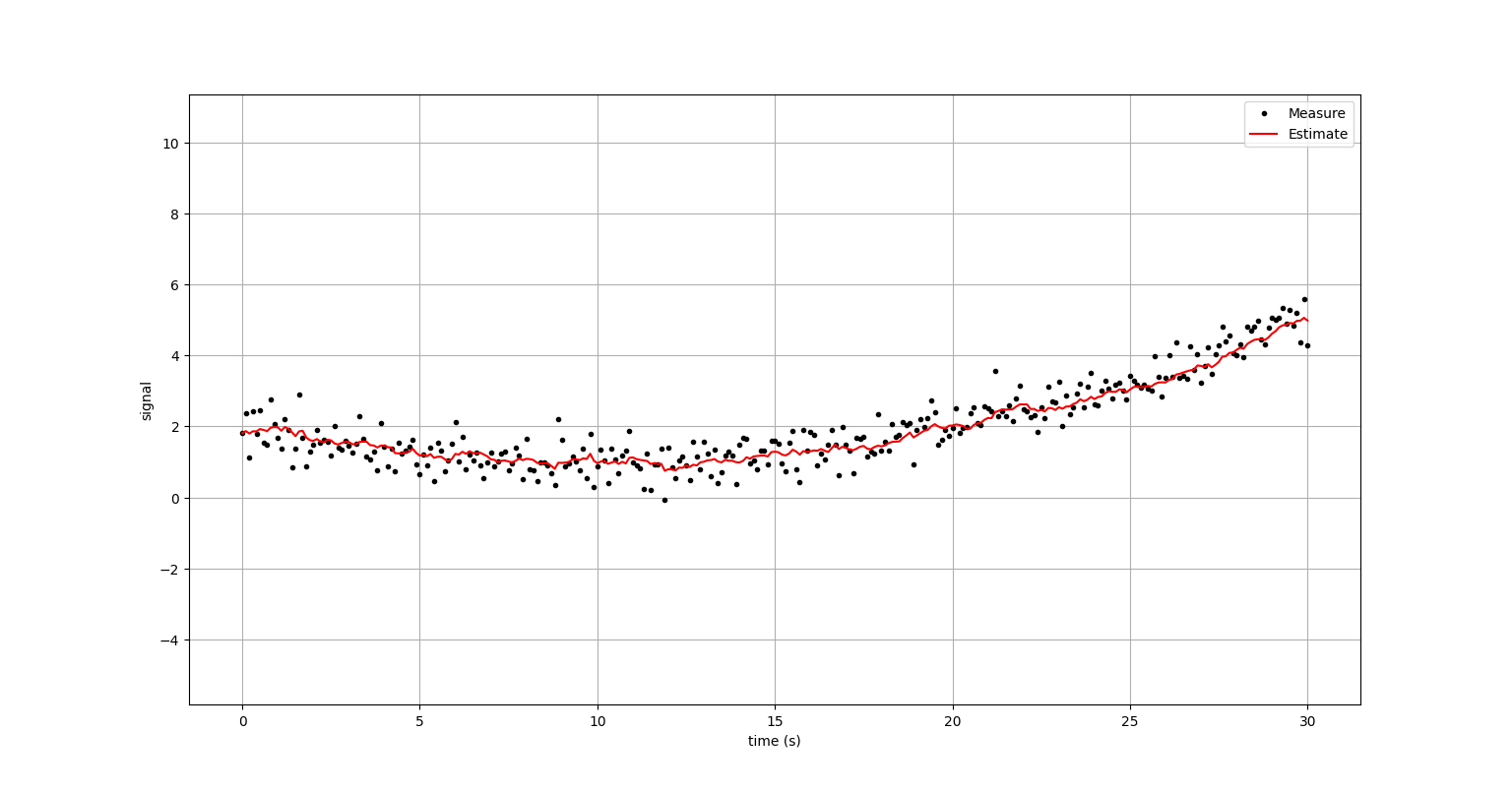

3. Low Pass Filter (저주파통과필터)

• Low pass란?

  • (파장이 짧은)고주파 성분을 제거하고, (파장이 긴)저주파 성분을 통과시킨다.
  • 데이터의 잡음을 제거하고 핵심적인 저주파 성분 데이터의 양상을 파악하기 위해 사용한다.

• 평균 필터들의 단점을 보완하고자 데이터의 가중치를 조절할 수 있도록 설계한 필터

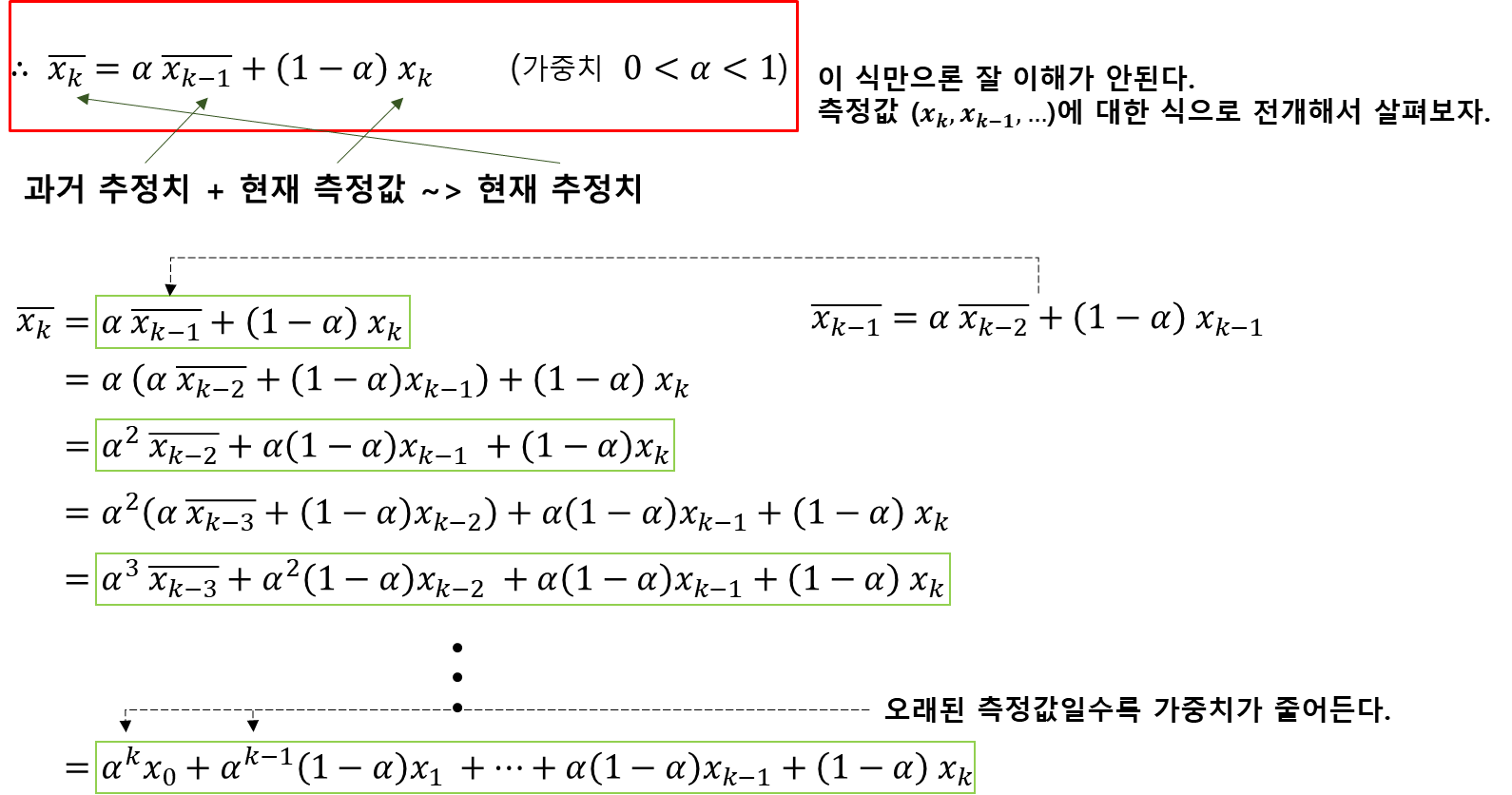
• Ex03) LowPassFilter.py

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 저주파통과필터 클래스
class LowPassFilter:
    def __init__(self, y_initial_measure, alpha=0.9):
        self.y_estimate = y_initial_measure
        self.alpha = alpha
 
    def estimate(self, y_measure):
        self.y_measure = y_measure
        self.y_estimate = self.alpha * self.y_estimate + (1 - self.alpha) * self.y_measure


if __name__ == "__main__":
    signal = pd.read_csv("Data/example_Filter_3.csv")

    y_estimate = LowPassFilter(signal.y_measure[0])

    for i, row in signal.iterrows():
        y_estimate.estimate(signal.y_measure[i])
        signal.y_estimate[i] = y_estimate.y_estimate

    print(signal)

    plt.figure()
    plt.plot(signal.time, signal.y_measure,'k.',label = "Measure")
    plt.plot(signal.time, signal.y_estimate,'r-',label = "Estimate")
    plt.xlabel('time (s)')
    plt.ylabel('signal')
    plt.legend(loc="best")
    plt.title("alpha=0.9")
    plt.axis("equal")
    plt.grid(True)
    plt.show()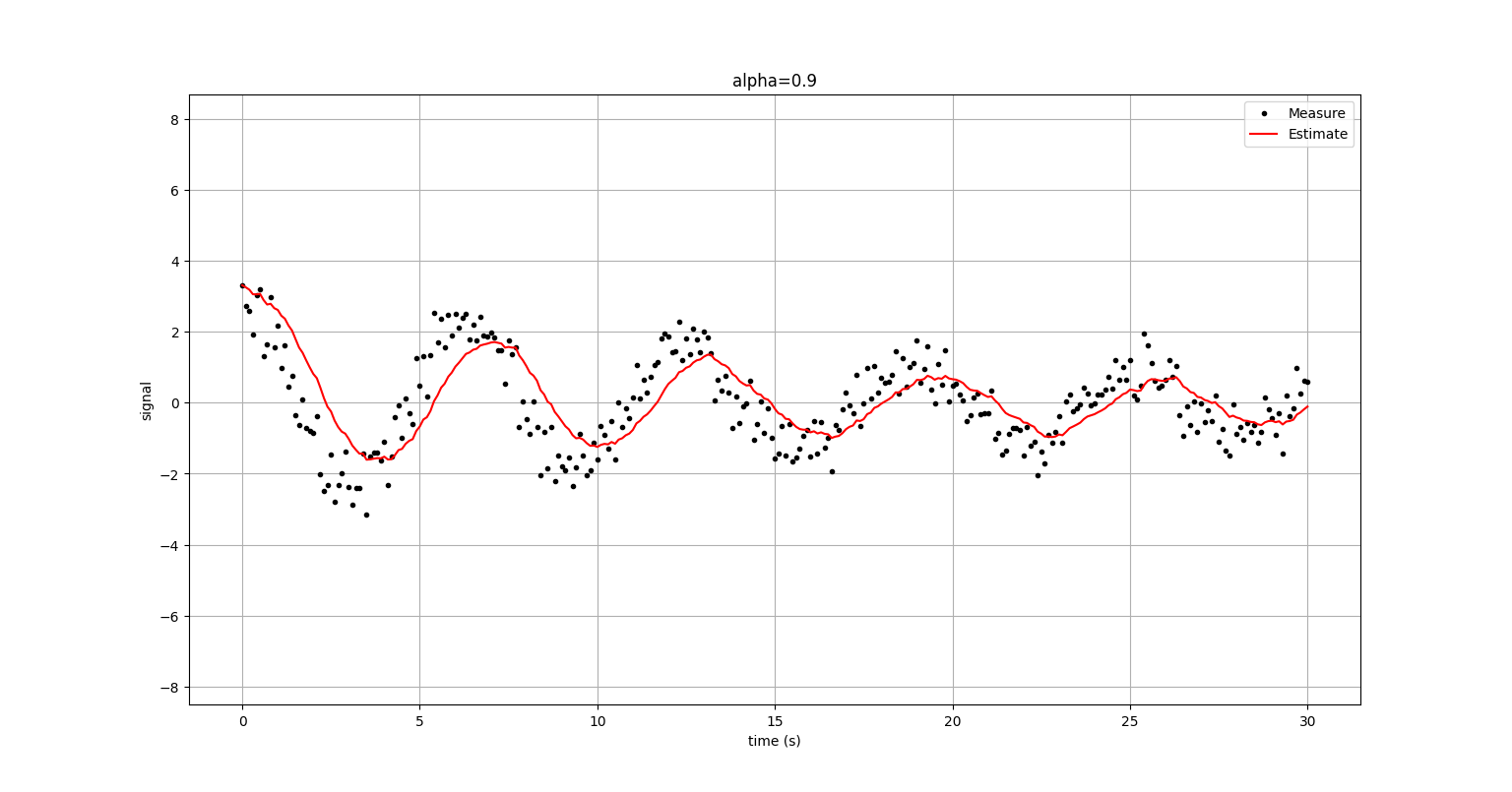

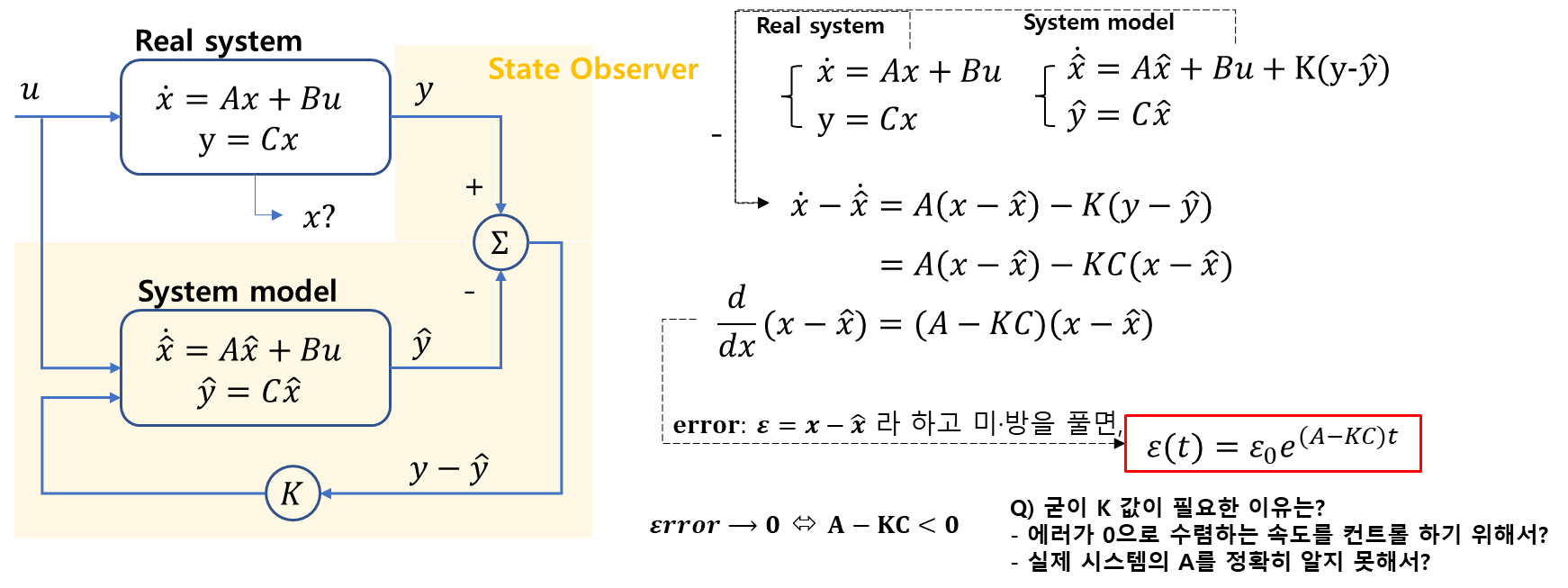
4. State Observers (State Estimator)

• 상태관측기는 직접측정할 수 없는 시스템의 정보를 간접측정을 통해 추정한다.

  • Real system의 measuered state를 알 수 없을 때, system의 수학적 model로 부터의 estimated state를 계산한다.

  • 두 state의 차이를 minimize 시키는 것이 제어의 목적이다.

  • Gain값을 어떻게 제어해야 할 지?
    ~> Kalman Filter는 확률 시스템으로 접근

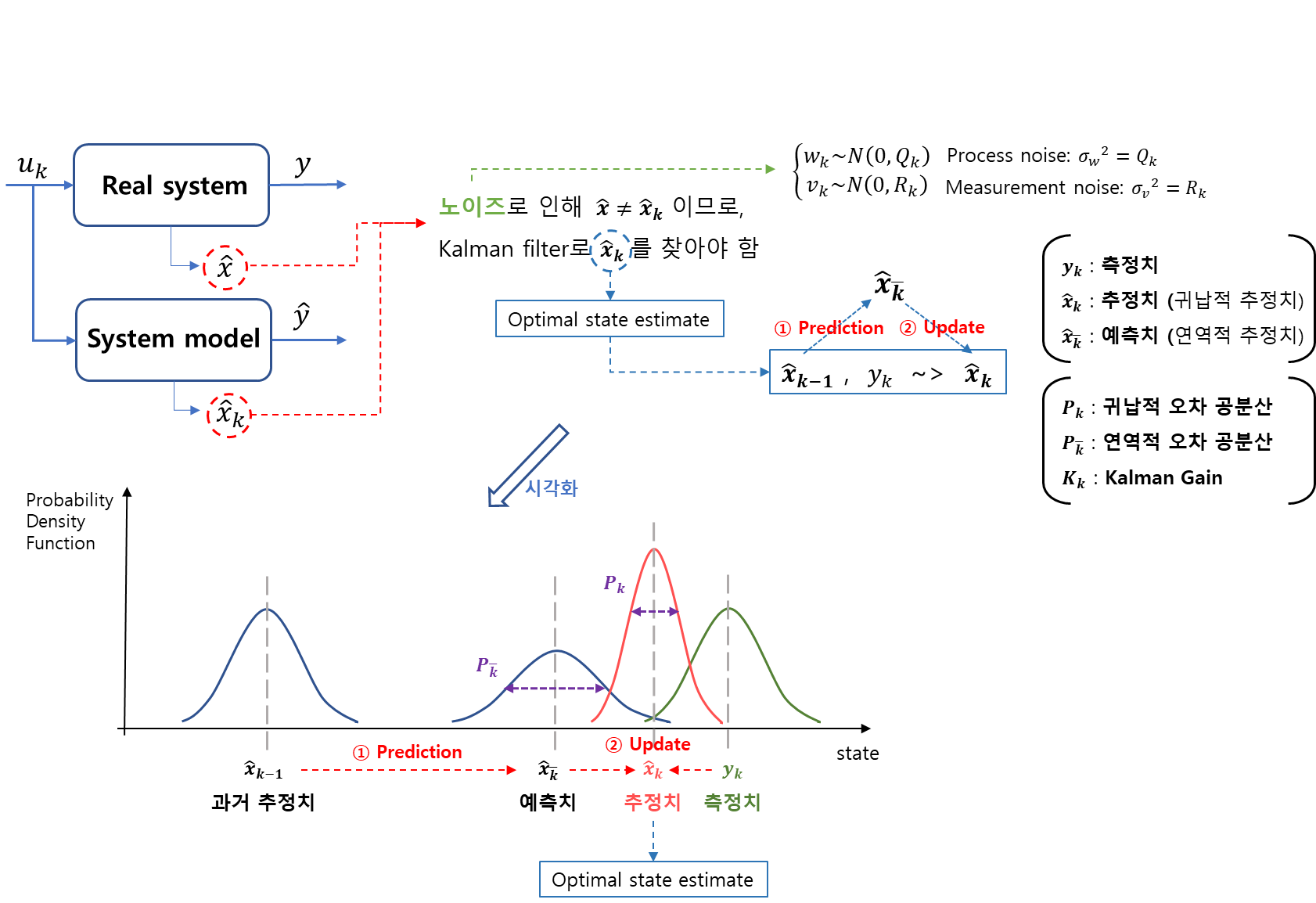
5. Kalman Filter

• Kalman Filter도 상태관측기의 한 종류이다.

• 과거의 귀납적 추정치 + 측정치를 이용해 현재의 귀납적 추정치를 구한다.

• Kalman Filter는 두 단계로 작동한다.

  • Step1) Predection

    • 과거의 귀납적 추정치로 현재의 연역적 추정치를 구한다
    • 연역적 오차공분산을 구한다.

  • Step2) Update

    • 현재의 귀납적 추정치를 구한다.

    • 귀납적 오차공분산을 구한다.

    • Kalman Gain을 구한다. Kalman Gain은 귀납적 오차공분산을 최소화 하기 위해 계산된다.

• Kalman Filter 시각화(?)

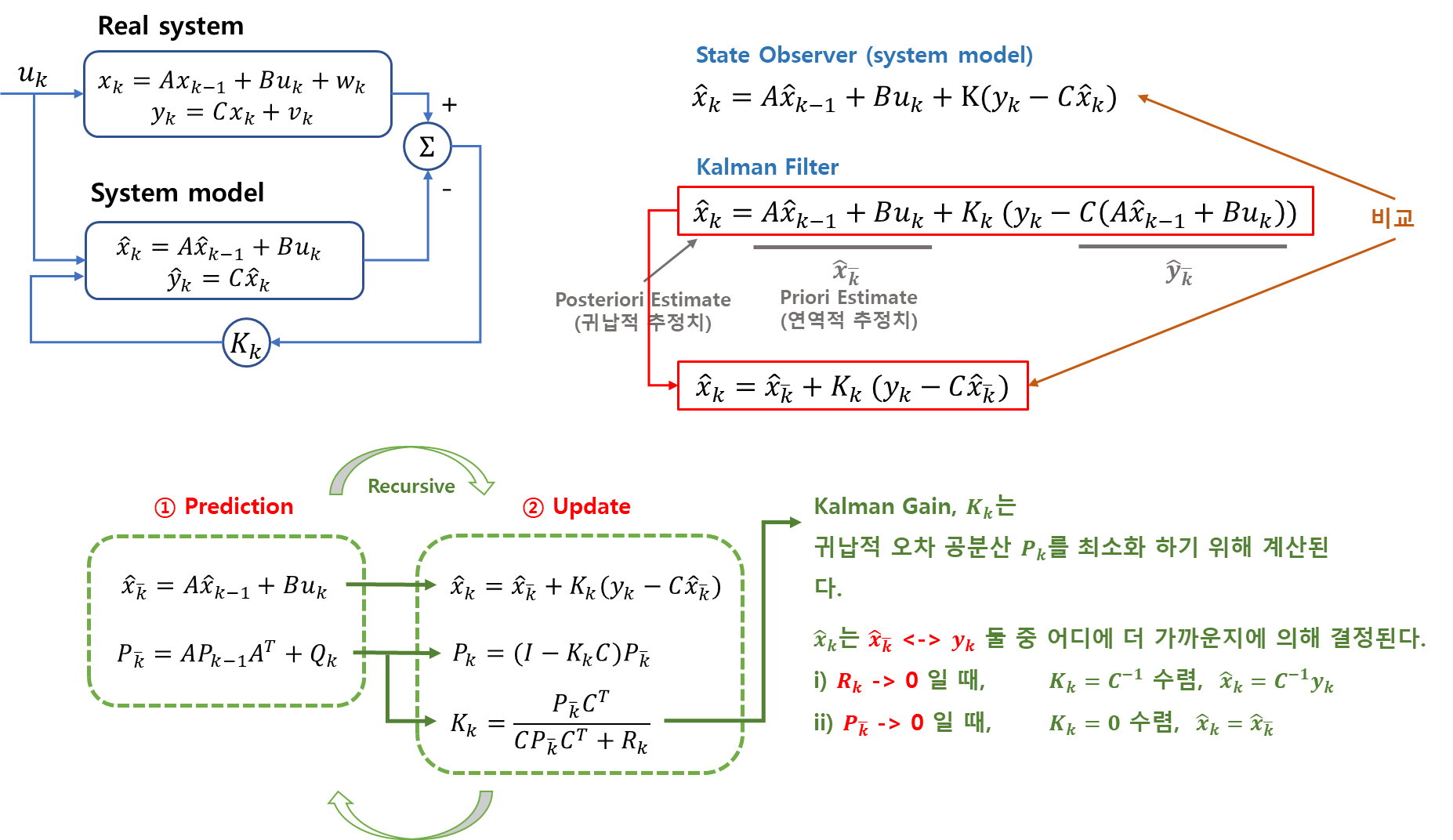
• Algorithm 방정식

• Ex04) KalmanFilter.py

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 칼만필터 클래스
class KalmanFilter:
    # model_variance: Q / measure_variance: R / error_variance_init: Px 초기값
    def __init__(self, y_measure_init, step_time=0.1, m=0.1, model_variance=0.01, measure_variance=1.0, error_variance_init=10.0):
        # A: state matrix
        self.A = np.array([1.0])
        # B: input matrix
        self.B = step_time / m
        # C: output matrix
        self.C = np.array([1.0])
        # D: direct transmission matrix
        self.D = np.array([0.0])
        # process noise 표준편차
        self.Q = model_variance
        # measurement noise 표준편차
        self.R = measure_variance
        # 초기 귀납적 추정치 = 측정치
        self.x_estimate = y_measure_init
        # Px: 초기 귀납적 오차 공분산
        self.P_estimate = error_variance_init

    def estimate(self, y_measure, input_u):
        # ****************** Prediction (귀납적 추정치 => 연역적 추정치 구하기) ******************
        # 연역적 추정치
        x_predict = self.A * self.x_estimate + self.B * input_u
        # 연역적 오차 공분산
        P_predict = self.A * self.P_estimate * self.A.T + self.Q

        # ****************** Update (연역적 추정치 + 측정치 => 귀납적 추정치 구하기) ******************
        # Kalman Gain
        K = P_predict * self.C.T / (self.C * P_predict * self.C.T + self.R)
        # 귀납적 추정치 (결국 이걸로 계산된 값이 최종 추정치로서 결과에 반영된다.)
        self.x_estimate = x_predict + K * (y_measure - self.C * x_predict)
        # 귀납적 오차 공분산 / np.eye(n) => nxn 크기의 identity matrix / A.shape[0] => A의 행의 개수 / A.shape[1] => A의 열의 개수
        self.P_estimate = (np.eye(self.A.shape[0]) - K * self.C) * P_predict


if __name__ == "__main__":
    # Load data (엑셀 데이터를 불러오고)
    data = pd.read_csv("Data/example_KalmanFilter_1.csv")
    # Initialize KalmanFilter (필터를 초기화 한다.)
    kalman_filter = KalmanFilter(data.y_measure[0])

    # Estimate data
    # 계산 전 dataFrame의 'y_extimate'열의 데이터들을 결측치로 초기화 해주는 것 np.nan
    data['y_estimate'] = np.nan
    # 행, 열 수 만큼 반복 (y_estimate의 계산값을 update한다.)
    for i, row in data.iterrows():
        # KalmanFilter 클래스의 estimate 메소드를 사용하여 data의 y_measure, u열의 두개의 값으로 y_estimate를 계산하여 반환한다.
        kalman_filter.estimate(row['y_measure'], row['u'])
        # 반환 된 값을 y_estimate 열의 i번 째 행에 넣는다.
        data.at[i, 'y_estimate'] = kalman_filter.x_estimate

    print(data)

    # Plot results
    plt.figure('ex04_KalmanFilter')
    plt.plot(data.time, data.y_measure, 'k.', label="Measure")
    plt.plot(data.time, data.y_estimate, 'r-', label="Estimate")
    plt.xlabel('Time (s)')
    plt.ylabel('Signal')
    plt.legend(loc="best")
    plt.axis("equal")
    plt.grid(True)
    plt.show()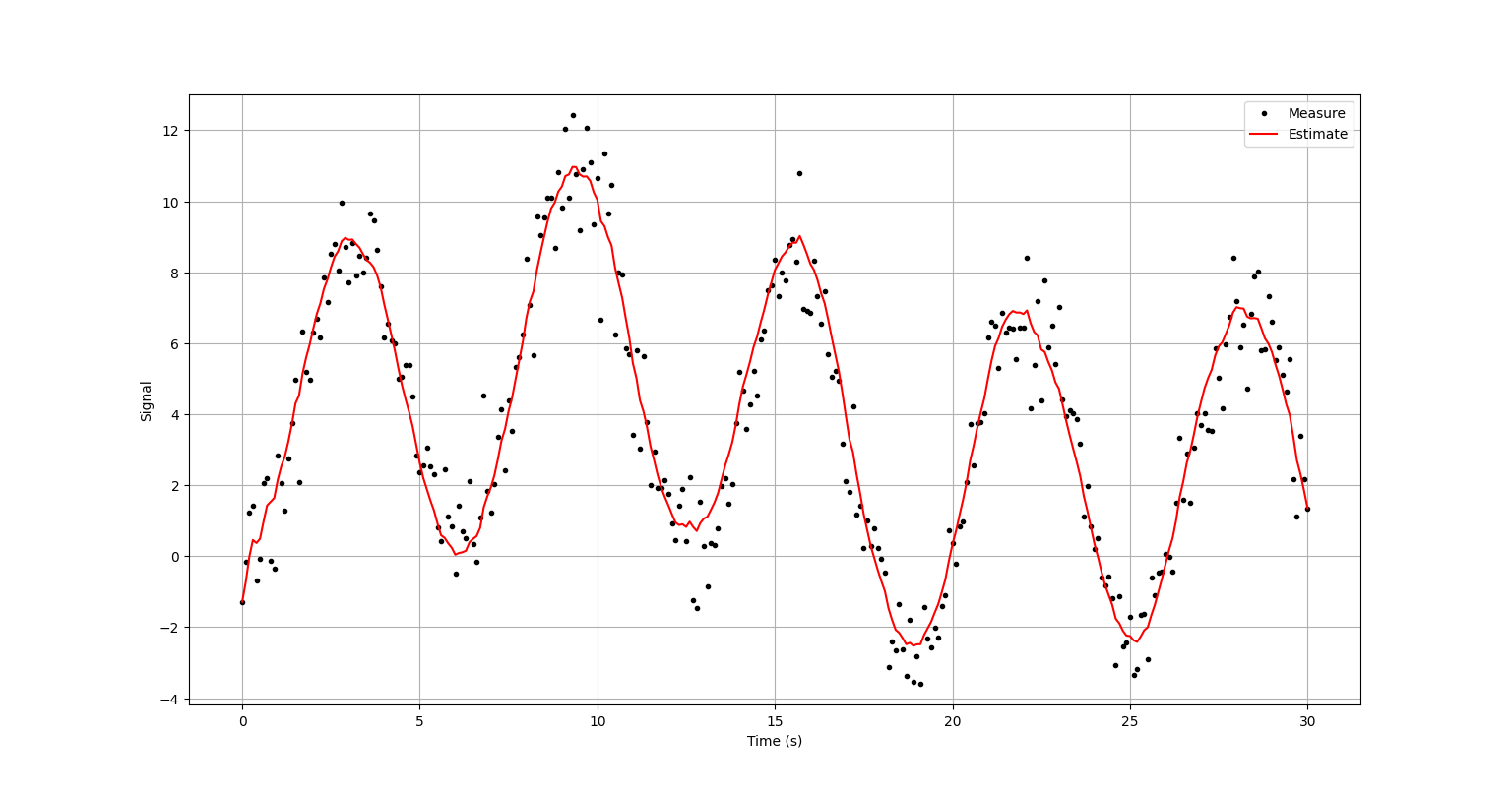

• Ex05) ComparingFilters.py

# 앞에서 작성한 각 Filter class 들을 가져와서 사용한다.
from ex01_AverageFilter import AverageFilter
from ex02_MovingAverageFilter import MovingAverageFilter
from ex03_LowPassFilter import LowPassFilter
from ex04_KalmanFilter import KalmanFilter
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import queue


if __name__ == "__main__":
    # 각 필터들에 대한 결과를 리스트로 저장한다.
    t = []
    y_AF = []
    y_MAF = []
    y_LPF = []
    y_KF = []
    
    # signal 이라는 인스턴스에 시험 데이터를 저장한다.
    signal = pd.read_csv("Data/example_KalmanFilter_1.csv")

    # instantiate filters
    # 각각의 class를 사용하여 필터 가동하여 y_extimate 저장할 인스턴스 생성
    y_estimate_AF = AverageFilter(signal.y_measure[0])
    y_estimate_MAF = MovingAverageFilter(signal.y_measure[0])
    y_estimate_LPF = LowPassFilter(signal.y_measure[0])
    y_estimate_KF = KalmanFilter(signal.y_measure[0])

    
    for i, row in signal.iterrows():
        # append(): 리스트 맨 뒤에 새로운 요소를 추가하는 함수
        t.append(signal.time[i])
        # Averageg filter의 추정치 리스트 채우기
        y_estimate_AF.estimate(signal.y_measure[i])
        y_AF.append(y_estimate_AF.y_estimate)
        # Moving Average filter의 추정치 리스트 채우기
        y_estimate_MAF.estimate(signal.y_measure[i])
        y_MAF.append(y_estimate_MAF.y_estimate)
        # Low pass filter의 추정치 리스트 채우기
        y_estimate_LPF.estimate(signal.y_measure[i])
        y_LPF.append(y_estimate_LPF.y_estimate)
        # Kalman filter의 추정치 리스트 채우기
        y_estimate_KF.estimate(signal.y_measure[i],signal.u[i])
        # KalmanFilter의 계산결과가 2차원 array로 나와 plot이 불가 => item()함수 사용하여 다차원 요소를 scalar 값으로 변환
        y_KF.append(y_estimate_KF.x_estimate.item())

    # print(y_AF)
    # print(y_MAF)
    # print(y_LPF)
    # print(y_KF)  

    plt.figure("ex05 Comparing Filter")
    plt.plot(signal.time, signal.y_measure,'k.',label = "Measure")
    plt.plot(t, y_AF,'m-',label = "Average Filter")
    plt.plot(t, y_MAF,'b-',label = "Moving Average Filter")
    plt.plot(t, y_LPF,'c-',label = "Low Pass Filter")
    plt.plot(t, y_KF,'r-',label = "Kalman Filter")
    plt.xlabel('time (s)')
    plt.ylabel('signal')
    plt.legend(loc="best")
    plt.axis("equal")
    plt.grid(True)
    plt.show()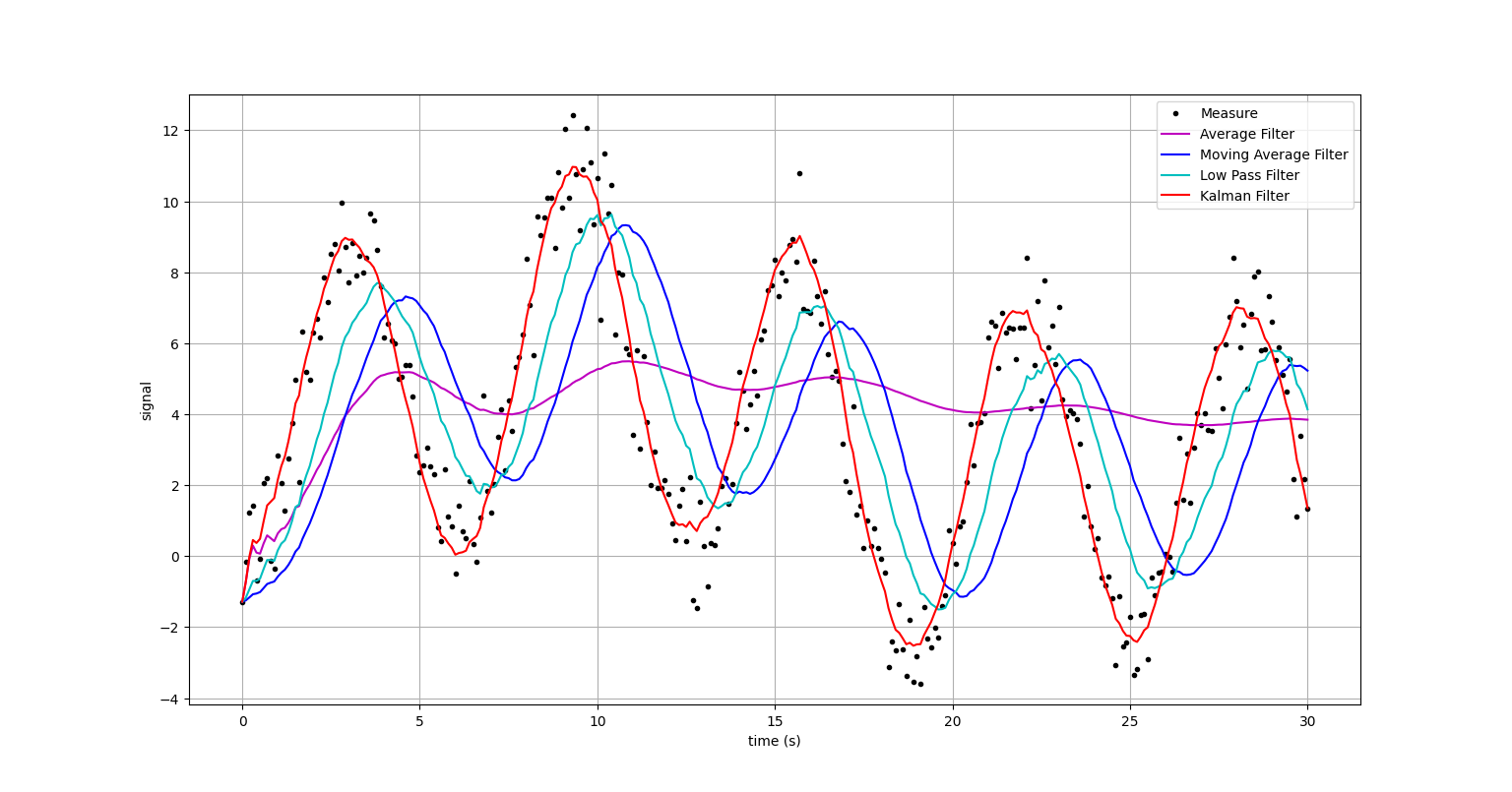

[4] PID Control

• P control: 현재 error에 대해서만 반응

  • 한계: error가 작을 때 원하는 출력을 충분히 내지 못할 수 있다.

• I control: 오차를 누적시켜 작은 오차에 대해서도 충분한 출력을 낼 수 있다.

  • 한계: 오차 누적(Error Acuumulation)을 해결하기 위해 오차가 더해지는 한계를 정해 reset 해줘야 한다. (적분 누적 방지법: Integral Anti-Winde up 필요)

• D control: P 제어기로만은 수렴하지 않던 시스템을 PD 제어로 수렴시킬 수 있고, 더 나아가 Overshoot을 제어할 수 있다.

• 더 자세한 내용은 학부 때 배운 자동제어 수업 자료 참고하기~

• PID control 과제를 통해 python으로 직접 구현해 보면서 해당 이론을 더 잘 이해할 수 있는 기회가 되었다.

---

출처
(1) Programmers K-Digital-Training: 자율주행 데브코스 Planning & Control, 고전제어
(2) 칼만 필터의 이해, youtude,
https://www.youtube.com/watch?v=GfdMKISLRRk&list=PLH1vM2UZr5n9ceEAsgJb20xNLowGEgOqI&index=1
(3) Katsuhiko Ogata, 시스템해석, Pearson-교보문고(2018)