😃[5주차 - Day1]😃

Machine Learning
경험을 통해 자동으로 개선하는 컴퓨터 알고리즘의 연구!
학습데이터 : 입력벡터들 x1, ... , xN, 목표값들 t1, ... , tN
머신러닝 알고리즘의 결과는 목표값를 예측하는 함수 y(x)를 구하는 것입니다.
핵심 개념들
학습단계 : 함수 y(x)를 학습데이터에 기반해 결정하는 단계
시험셋 : 모델을 평가하기 위해서 사용하는 새로운 데이터
일반화 : 모델에서 학습에 사용된 데이터가 아닌 이전에 접하지 못한 새로운 데이터에 대해 올바른 예측을 수행하는 역량
지도학습 : target이 주어진 경우
- 분류 (classification)
- 회귀 (regression)비지도학습 : target이 없는 경우
- 군집 ( clustering )다항식 곡선 근사 ( Polynomial Curve Fitting)
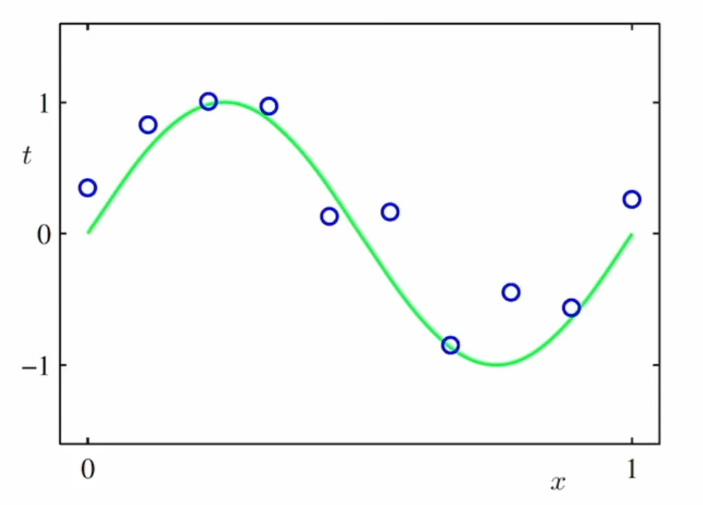
학습데이터 : 입력벡터 X = (x1, ... , xN)T, t = (t1, ... , tN)T <- T는 Transpose (열벡터로 전환)
확률이론 : 예측값의 불확실성을 정량화시켜 표현할 수 있는 수학적인 프레임워크
xhat이 주어졌을 때, 목표값 that을 예측하는 것이 목표입니다.
이런것을 해결하기 위하여 확률이론과 결정이론을 활용하여 최적의 예측을 수행할 수 있는 방법론을 제시합니다.
우리가 사용할 함수 y는 아래와 같은 형태를 가지게 됩니다.
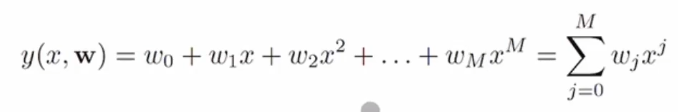
위와 같은 함수에서 x는 입력, w는 우리가 찾아야 할 목표입니다. x에 관해서는 다항식입니다. 하지만 모델의 파라미터 w에 대해서는 선형식입니다. x는 데이터에서 주어지는 바뀌는 값이고, w는 알지는 못하지만 고정되어 있는 값인데 이를 찾아내는 것이 목표입니다.
오차함수 (Error Function)
데이터가 주어져 있을 때 계수 w를 찾는것이 목표인데, 주어진 w에 대한 함수값 y와 데이터 t 사이의 차이를 표현한 것이 오차함수입니다.
오차함수들 중에서 가장 일반적인 함수는 제곱합 함수입니다.
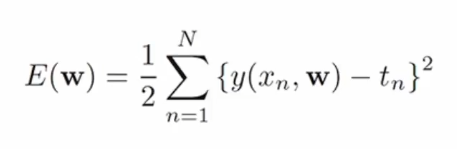
과소적합(Under-fitting)과 과대적합(Over-fitting)
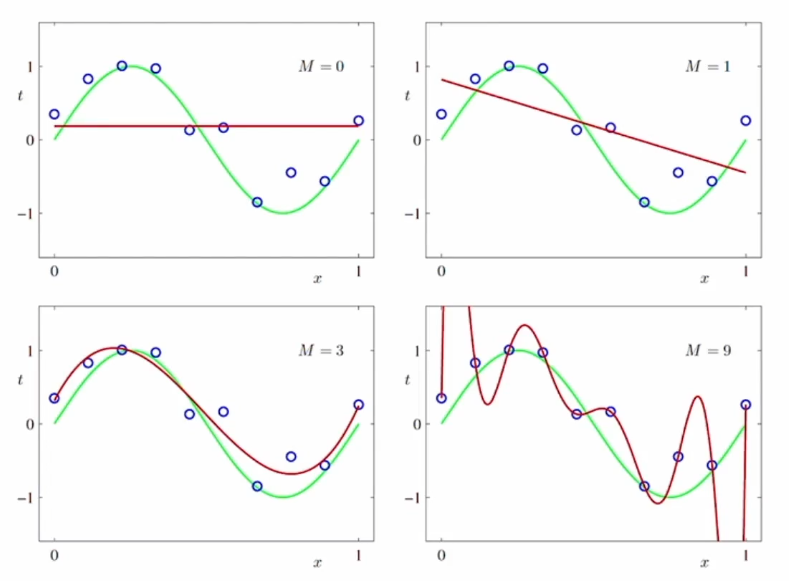
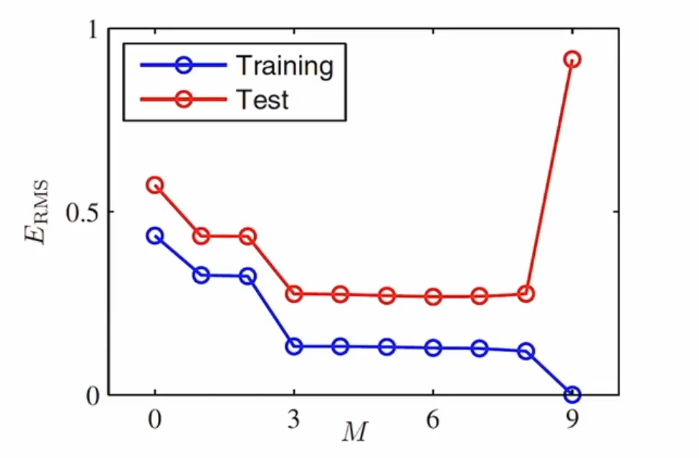
M=0, 1일 경우, 과소적합한 오차함수를 만들어 내었고, M=9일 경우, 과대적합되었다고 말할 수 있습니다. 데이터의 노이즈 까지 과하게 적용했다는 뜻입니다.
과소적합 및 과대적합이 일어나는 것을 어떻게 판단할 수 있는가를 살펴보면, 이는 일반화에 관한 문제이고 새로운 데이터에 관한 문제입니다. 그러므로 새로운 데이터가 들어왔을 때, 얼마나 이 함수가 예측을 잘 하는가를 살펴보면 됩니다.
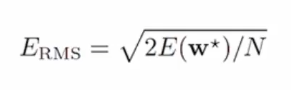
위와 같은 식으로 판단해 볼 수 있습니다. M이 적합한 위치로 갈 수록, 위의 식의 오류값이 작게 나타나는 것을 알 수 있습니다.
데이터의 개수가 많아지면 많아질수록, 과대적합의 모델도 사용할 수 있는것을 추론적으로 알게됩니다. 이는 아래의 그림을 보면 알 수 있는데, 데이터가 많아질수록 빨간 그래프가 매끄럽게 그려지는 것을 볼 수 있습니다.
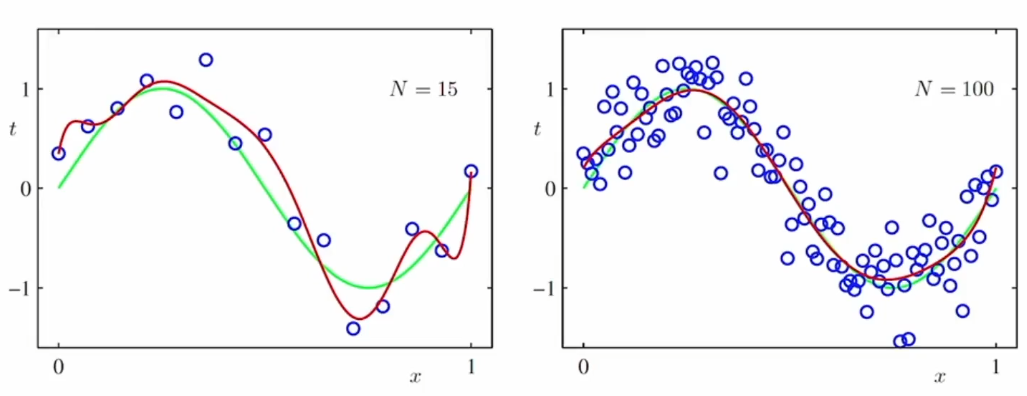
고로, 모든 머신러닝 프로젝트들의 목표가 많은 양의 데이터를 수집하는 것입니다.
규제화를 통해 과대적합을 막을 수 있는데, 이 값이 너무 크다면 또다시 과소적합이 될 수 있는 위험성이 있습니다.
확률이론
확률변수 (Random Variable)
확률변수 X는 표본의 집합 S의 원소 e를 실수갑 X(e) = x에 대응시키는 함수입니다.
동전을 2개 던지는 경우를 생각해봅니다.
Head, Tail 두 가지 경우가 있을텐데,
X(HH) = 2, X(HT) = 1, X(TH) = 1, X(TT) = 0 인 경우,
P[X=1] 인 경우 P[{HT, TH}] = 2/4 = 1/2의 확률을 가진다고 할 수 있습니다.
또한, P[X<=1] = P[{HT,TH,TT}] = 3/4 의 확률입니다.
연속확률변수 (Continuous Random Variable)
누적분포함수(cumulative distribution function)
CDF라고도 부르는데, 확률변수 X가 어떤 범위 안에 있을 확률을 나타내는 함수입니다.
누적분포함수 F(x)를 가진 확률변수 X에 대해서
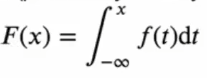
위와 같은 함수 f(x)가 존재한다면, X를 연속확률변수라고 하고, f(x)를 X의 확률밀도함수(probability density function, pdf)라고 부릅니다.
확률변수의 성질
덧셈법칙, 곱셈법칙, 베이즈 확률
확률변수의 함수

위와 같은 문제에서 살펴본다면,
밑의 두개의 식이 관계를 정의하고 있습니다. 벡터 y의 pdf를 찾는 것인데,
야코비안? 을 찾는 것이 먼저입니다.
네 개의 편미분 식을 구해서 행렬식을 계산하면 됩니다.
하나하나 대입을 해보면, 아래와 같이 작성됩니다.
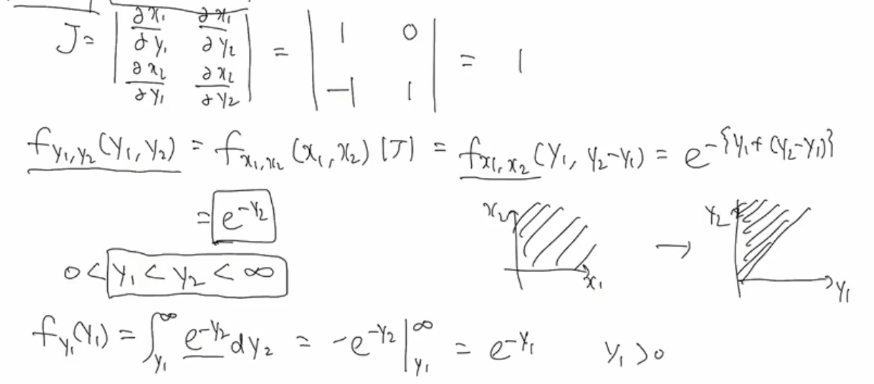
위와 같은 일을 하는 이유에 대한 예시를 알아보자면,

위와 같은 예시를 사용할 수 있습니다. 이는 Inverse CDF technique을 사용하여 해결할 수 있습니다. 원이 있고 어떤 점이 찍어졌을 때, 그 세타값과 d값을 구하면 이를 해결할 수 있습니다. 세타는 0부터 2파이까지 가능하지만, d값을 구하는 것이 막막합니다.
그러므로 d값의 cdf부터 생각해본다면 이를 해결할 수 있습니다.
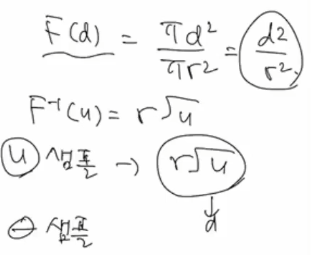
위와 같이 구하면, 점 하나를 구할 수 있게되고 이를 여러개 생성하면 문제를 해결할 수 있습니다.
기댓값 (Expectations)
확률분포 p(x)하에서 함수 f(x)의 평균값
이산확률분포, 연속확률분포
확률분포로부터 N개의 샘플을 추출해서 기댓값을 근사할 수 있다.
조건부 기댓값이라는 개념도 존재합니다.
분산 (Variance), 공분산 (Covariance)
f(x)의 분산: f(x)의 값들이 기댓값 E(f)로부터 흩어져 있는 정도를 표현합니다.
아래의 식과 같이 표현할 수 있는데요.
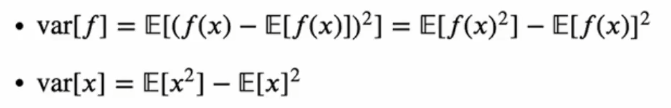
첫째식에서 풀어 써보면 마지막 식과 같이 표현이 됩니다.
두 개의 확률변수 x,y에 대한 공분산은 다음과 같이 표현할 수 있습니다.
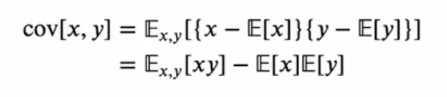
확률을 해석하는 두 가지 관점
빈도주의
반복가능한 사건들의 빈도수에 기반하여 확률을 해석합니다.
베이지안
이와는 다르게 불확실성을 정량적으로 표현합니다.
e.g. 반복가능하지 않은 사건 : 북극얼음이 이번 세기말까지 녹아 없어질 확률과 같은 것
빈도주의 vs 베이지안
모델의 파라미터 w에 대해 지식을 확률적으로 나타내고 싶다면?
w에 대한 사전지식 p(W) => 사전확률(prior)과
새로운 데이터 D = {t1, ... , tn} 를 관찰하고 난 뒤 조건부확률 p(D|w)를 우도함수 (likelihood function) 이라고 합니다.
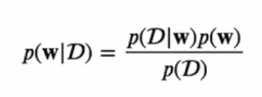
그렇게 되면 p(w|D) 라는 사후확률을 구할 수 있습니다. 이는 w에 대한 불확실성을 표현할 수 있습니다.
베이지안 관점의 장점은 사전확률을 모델에 포함시킬 수 있습니다. 이는 동전을 던져서 세번 다 앞면이 나올 확률을 생각해본다면, 3번 모두 앞면이 나올 가능성이 현실에서는 충분히 존재합니다.
이를 최대우도의 방식인 빈도주의 관점에서는 그 다음에 동전이 나올 확률은 1이 될 수 밖에 없지만, 이는 상식적으로 동전이 나올 확률은 반반이라는 것을 알고 있기에 베이지안에서 더 나은 추리를 할 수 있게 됩니다.
정규분포
추후에 다음 강의들에서 자세히 다루겠지만,
형태는 다음과 같습니다. 뮤와 시그마가 정규분포의 파라미터가 됩니다.
가우시안 분포가 정규화됨(normalized)을 보일 것입니다. 즉,
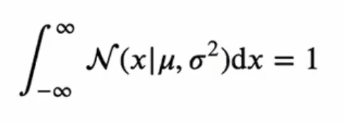
확률밀도함수가 주어졌을 때, 위 성질을 만족시키면 (음의 무한대에서 양의 무한대까지 적분했을때 1이 된다면) 정규화되었다고 합니다.
모든 pdf는 위와 같은 성질을 만족시켜야 합니다. 이것이 성립한다는 것에 대한 증명입니다.
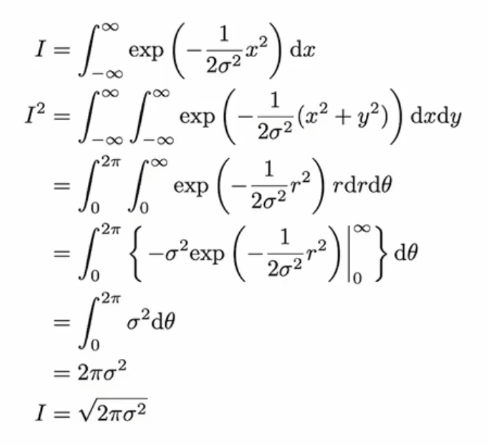
뮤가 0인 형태를 예시로 보겠습니다.
정규분포가 주어졌을 때 그 기댓값
E[x] = mu
증명 :
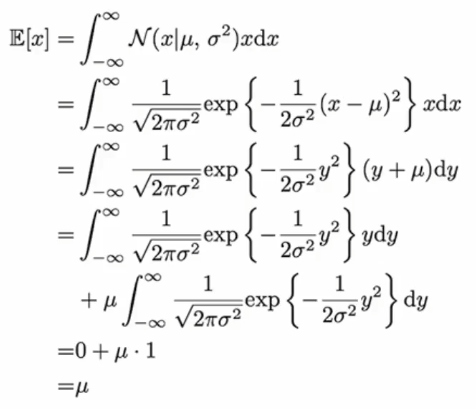
정규분포가 주어졌을 때 그 분산
var[x] = y = sigma^2
정규분포가 주어졌을 때 최대우도해
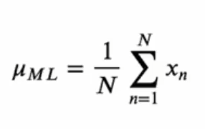
곡선 근사 (Curve Fitting)
학습 데이터 : X = (x1, ... , xN)T, t = (t1, ... , tN)T
우도함수를 최대화 시키는 것은 제곱합 오차함수를 최소화 시키는 것과 동일합니다.
베이지안 곡선 근사
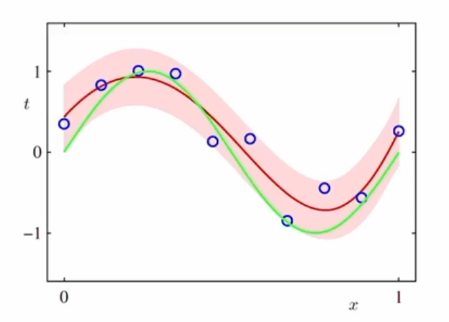
이러한 완전한 베이지안 근사를 통해서 목표값을 모델링하게 되면, 하나의 값이 아니고 어떠한 분포가 나타나게 됩니다.
t의 예측분포를 구하게 되면 어떠한 밴드가 생성이 되고 이 값들이 크게 벗어나지 않을거라 예상할 수 있습니다.
