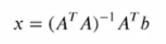😃[5주차 - Day4]😃

Linear Algebra
Norm
벡터의 길이. l2 norm 은 아래와 같이 표현할 수 있습니다.
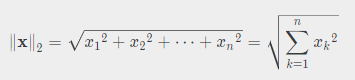
이는 각 벡터의 제곱합의 루트값인데요. 흔히 아는 크기의 값을 말합니다.
import numpy.linalg as LA
LA.norm(np.array([3,4]))이를 파이썬에서는 위와 같이 간단하게 표현할 수 있습니다.
이를 조금 더 일반화 시키면 lp norm 을 구할 수 있습니다.
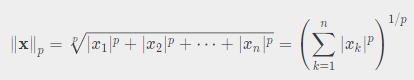
Frobenius norm은 아래와 같이 정의됩니다.
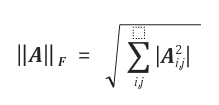
프로베니우스 놈은 Matrix에 대한 크기를 알 수 있습니다. 이 프로베니우스 놈은 ATA 의 trace값의 스퀘어(루트)와 같습니다.
행렬이 주어지게 되면 파이썬 코드에서 norm은 자동으로 프로베니우스 놈을 계산하게 됩니다.
A = np.array([
[100, 200, 300],
[ 10, 20, 30],
[ 1, 2, 3],
)]
LA.norm(A)
>>> 376.0505285
np.trace(A.T.dot(A))**0.5
>>> 376.0505285선형독립과 Rank
벡터들의 집합 {x1, x2, ... , xn} 에 속해 있는 어떤 벡터도 나머지 벡터들의 선형조합으로 나타낼 수 없을 때 이 집합을 선형독립이라고 하고, 역으로 어떤 벡터가 나머지 벡터들의 선형조합으로 나타난다면 이는 선형종속이라고 부릅니다.
예를들어,
A = np.array([
[1,4,2],
[2,1,-3],
[3,5,-1],
])위와 같은 행렬이 있을 때, Column의 집합은 종속입니다.
A[:,2] == -2*A[:,0] + A[:,1]위와 같은 등식이 성립하기 때문입니다.
여기서 Column rank와 Row rank에 대해 알아보겠습니다.
Column rank, Row rank
행렬의 열들의 부분집합 중에서 가장 큰 선형독립인 집합의 크기를 말하는데요, 위 A 행렬에서 이 크기는 2입니다.
또한 Column rank와 row rank는 동일하다는 결과가 있습니다. 따라서 단순히 rank를 표시할 경우는 rank(A)로 표현할 수 있습니다.
모든 행렬이 독립인 경우, 이를 Full rank라고 말합니다. Transpose 해도 같다는 것을 알 수 있습니다.
LA.matrix_rank(A)랭크를 구하기 위해 위의 코드로 간단하게 사용할 수 있습니다.
역행렬, 직교행렬 (Orthogonal Matrix)
간단하게, 쉽게 아는 개념입니다.
numpy 코드로는 아래와 같이 역행렬을 구할 수 있습니다.
LA.inv(A)또한, xTy = 0이 성립하는 두 벡터를 직교라고 부릅니다.
모든 열들이 서로 직교이고, 정규화된 정방행렬을 U라고 부른다면, 다음이 성립하게 됩니다.
UTU = I
UUT = I
U-1 = UT
||Ux||2 = ||x||2
치역(Range), 영공간(Nullspace)
A가 Rmxn 행렬일때,
치역은 A의 모든 열들에 대한 생성(span)이고, 이는 차원이 m입니다. 영공간은 A와 곱해졌을 때 0이 되는 모든 벡터들의 집합입니다. 이는 차원이 n인 집합입니다.
두개의 집합의 차원이 다른데, A의 Transpose의 치역을 구하면, n차원을 가지게 되고 A의 영공간과 차원이 같게 됩니다.
n차원 전체 공간에 있는 임의의 점을 하나 선택을 하면, 그 점을 A의 Transpose의 치역과 A의 영공간에 속하는 두개의 원소의 합으로 나타낼 수 있습니다.
투영(projection)
행렬 A의 치역 R(A)가 주어졌을 때, 그 공간위로 벡터를 투영시킨다면 A 공간 안에 있는 가장 가까운 점을 의미합니다.
Proj(y; A) = A(ATA)-1ATy
U에 대해 알아보자면, 임의의 y에 대해서는 Proj(y; U) = y입니다.
모든 y에 대해 위 식이 성립해야하므로, UUT = I (단위행렬) 입니다.
행렬식 (Determinant)
|A| (or det A) 라고 표현합니다.
만약
A = np.array([1, 2, 3],
[4, 5, 6],
[7, 8, 0])이 경우, 행렬식은 아래와 같이 구할 수 있습니다.
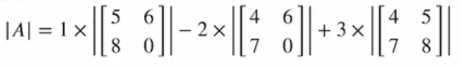
numpy를 사용한다면
LA.det(A)을 사용해서 간단하게 이를 계산할 수 있습니다.
이차형식 (Quadratic Forms)
고유값(Eigenvalues), 고유벡터(Eigenvectors)
정방행렬 A가 주어졌을 때, Ax = 람다x인 관계가 성립하고 x가 0이 아니라면 이것을 만족하는 람다 값을 행렬 A의 고유값이라고 하고, x값을 고유벡터라고 부릅니다.
람다값이 실수값이 아니라, 컴플렉스 넘버에 속하는 값입니다.
numpy에 있는 eig 함수를 사용하면 고유값을 구할 수 있습니다.
A = np.array([
[1, 2, 3],
[4, 5, 9],
[7, 8, 15]
])
eigenvalues, eigenvectors = LA.eig(A)
eigenvalues, eigenvectors
LA.matrix_rank(A)rank(A)는 0이 아닌 A의 고유값의 개수와 같다.
A가 non-singular일 때, 1/람다i는 A의 역행렬의 고유값입니다.
행렬미분 (Matrix Calculus)
머신러닝을 하다보면 대부분은 하나의 함수에 대한 미분이 아니고 엄청나게 많은 계수가 존재합니다. 이에 대한 미분이 필요합니다.
행렬 A를 입력받아서 실수값을 돌려주는 함수가 존재한다고 할 때,
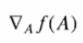
이러한 기호로 사용합니다. 각각의 함수값을 행렬의 ij값으로 편미분 해준 값이 각각의 값이 됨을 알 수 있습니다.
이에 대한 중요한 공식들이 존재합니다.
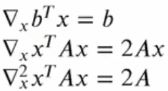
최소제곱법 (Least Squares)
mxn차원의 행렬 A가 주어져있고 n차원의 벡터 b가 주어져있을 때,
Ax=b를 만족하는 벡터 x를 찾을 수 없을 경우,
Ax가 b와 최대한 가까워지는 x를 구하는 문제입니다.