CS50 Probelm set 3 - Tideman 투표

dondonee·2023년 2월 14일

CS50

목록 보기

10/12

Tideman 투표

다수결 투표는 각 투표자가 하나의 후보자를 고르고, 가장 많은 표를 얻은 후보자가 승리하는 아주 단순한 시스템이다. 하지만 최다 득표자가 여러 명인 경우, 한 명의 승자를 뽑을 수 없다는 문제점이 있다.

이에 대한 대안으로 순위선택투표 시스템이 있다. 동점자가 있는 경우, 가장 적은 득표를 가진 후보를 제거하고 그 후보를 뽑은 투표자가 차선으로 뽑은 후보자에게 표가 던져지는 방식으로 결선을 하여 승자를 가려내는 방식이다. 또한 다수결 투표의 다른 잠재적인 결함도 예방할 수 있다.

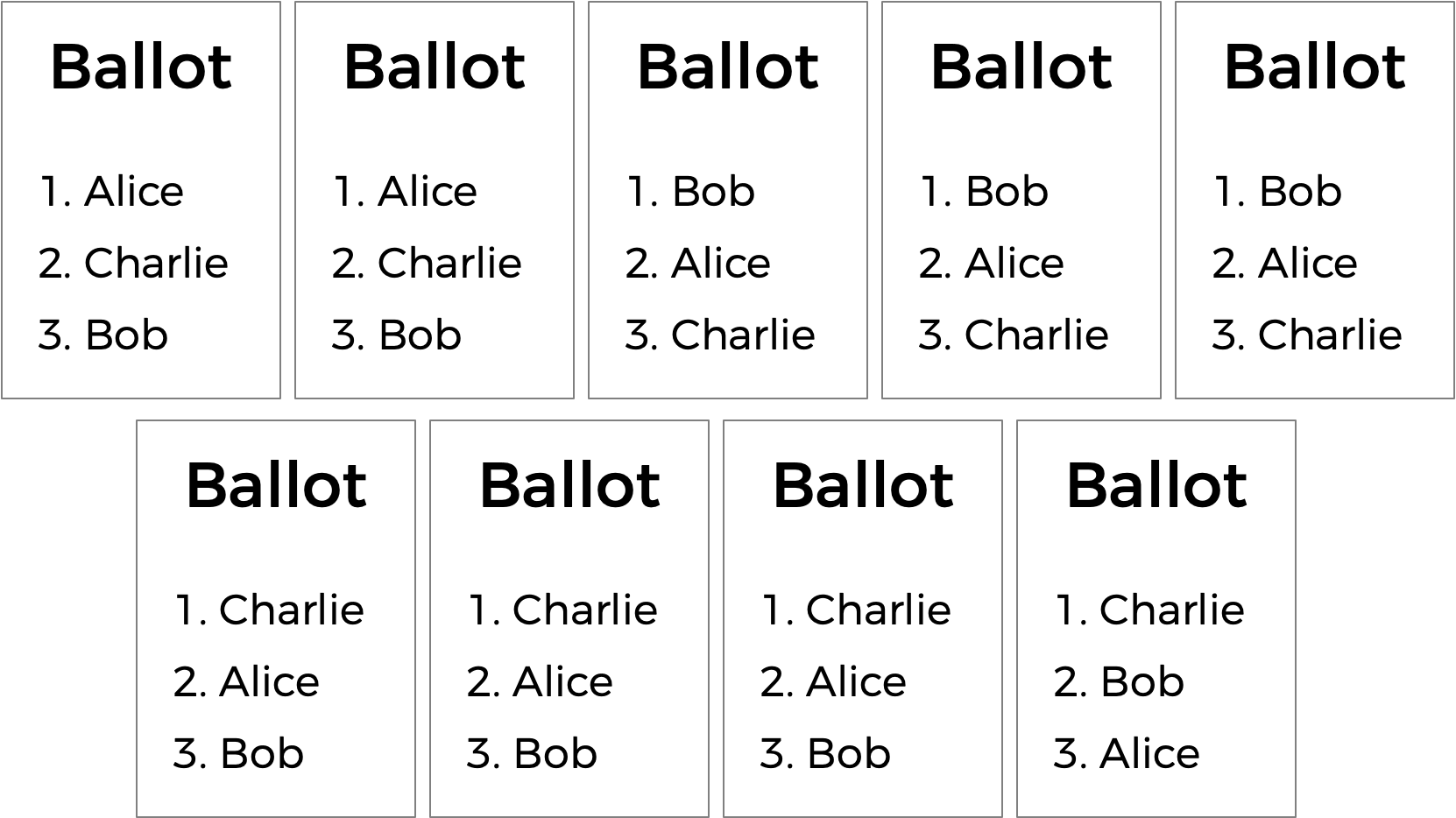
위와 같은 투표의 결과는 어떻게 될까? 다수결 투표 시스템에서는 4표를 얻은 Charlie가 승리하며, 즉각결선투표 시스템을 따른다고 해도 Charlie가 승리하게 된다. 하지만 Alice는 자신이 승자가 되어야 한다고 최종 변론할 여지가 있다. 9명 중 5명이 Charlie보다 Alice를 선호하기 때문이다.

이 투표에서 Alice는 이른바 ‘콩도르세 승자(Condorcet winner)’가 된다. 일대일 대결에서 항상 승리하는 후보자를 의미한다. Alice는 Bob과의 대결에서도, Charlie와의 대결에서도 항상 승리한다.

Tideman 투표 시스템은 콩도르세 승자가 존재할 경우 그 후보자가 승리할 수 있도록 보장하는 순위선택투표의 한 형태이다.

쉽게 설명하면 Tideman 투표 시스템은 화살표로 이루어진 후보자들의 ‘그래프’를 그리며 작동한다. 후보 A에서 B로 향하는 화살표는 A와 B의 일대일 대결에서 A가 승자임을 의미한다. 위 투표의 결과를 그래프로 나타낸 그림은 다음과 같다.

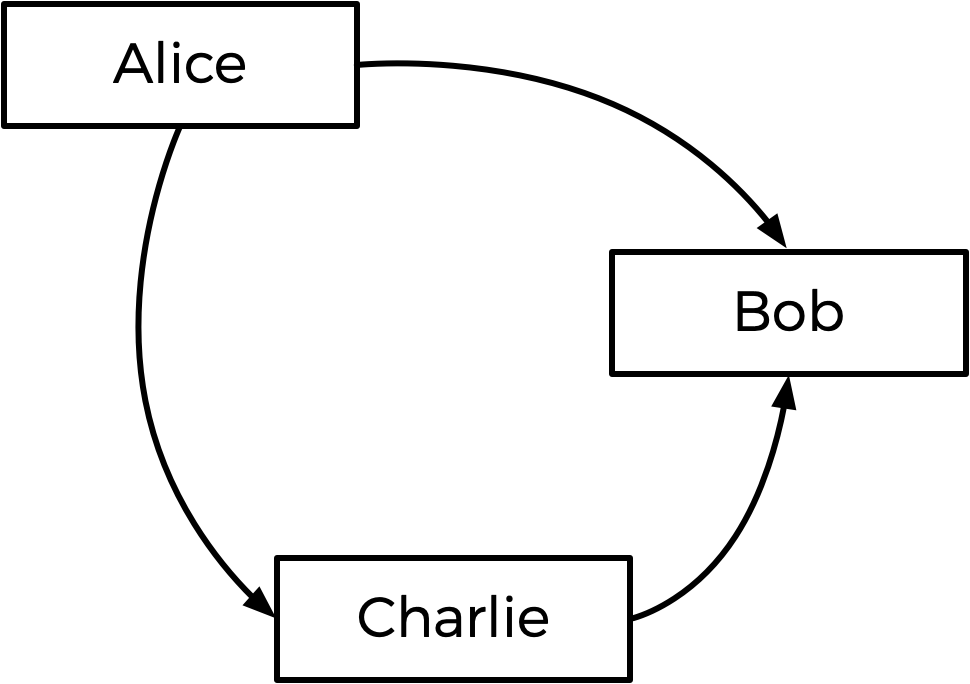
그래프의 ‘원천’이 되는 후보자가 승자가 된다. 어떤 화살표도 자신을 가리키지 않는, 즉 일대일 대결에서 항상 승리하는 후보자가 최종 승자이다. 따라서 이 투표의 승자는 Alice이다.

하지만 위와 같은 경우가 존재할 수 있다. 마치 가위바위보 게임처럼 모든 후보자를 이기는 승자가 없는 경우이다. Tideman 알고리즘은 이러한 사이클이 생기는 것을 방지해야 한다. 이를 위해서 가장 강력한 화살표부터 하나씩 고정시킨다. 사이클이 생기지 않으면 화살표를 추가하고, 사이클이 생긴다면 그 화살표는 무시한다.

Alice와 Bob의 일대일 결과는 7-2로, 가장 큰 격차를 가지므로 첫 번째로 고정되는 화살표가 된다. 그 다음으로는 6-3인 Charlie 대 Alice의 대결이 두 번째 화살표가 된다. 그 다음은 5-4인 Bob 대 Charlie의 대결인데, 이 화살표를 추가하면 그래프는 사이클이 생기게 된다. 그러므로 이 단계는 무시한다.

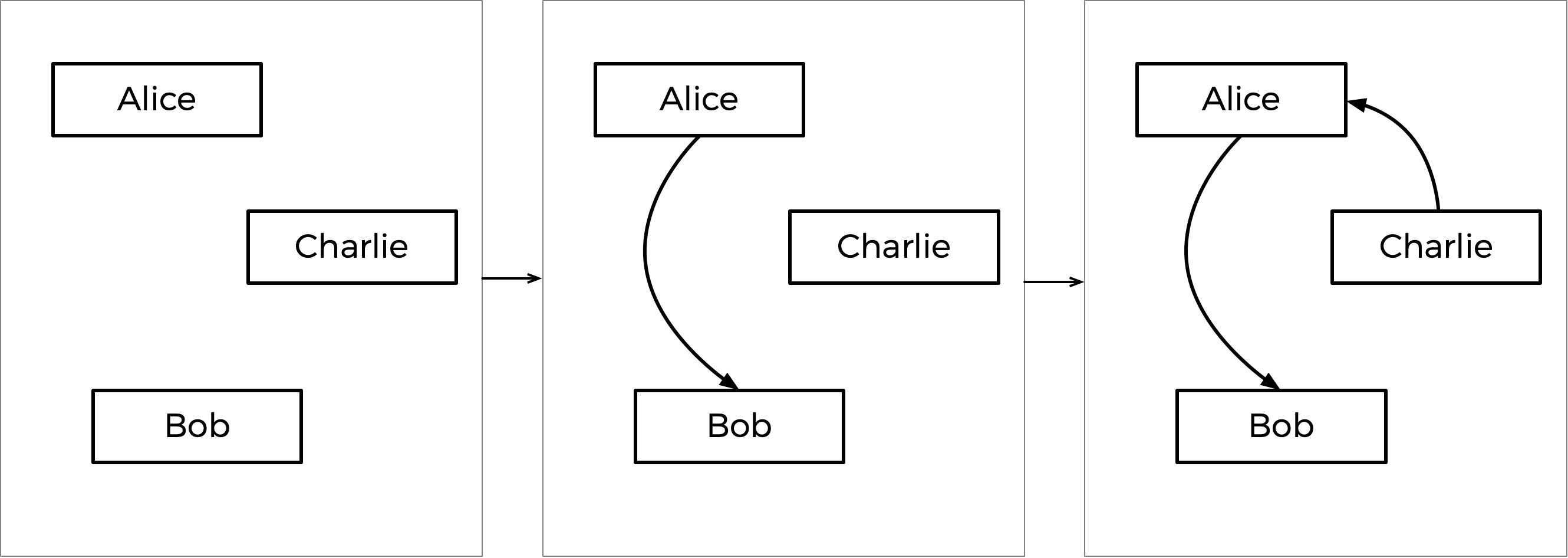
이 단계를 하나씩 그림으로 나타내면 위와 같다. Charlie를 가리키는 화살표가 없으므로, 즉 Charlie가 이 그래프의 ‘원천’이 되었기 때문에 승자는 Charlie가 된다.

정리하면 Tideman 투표 시스템은 세 가지 단계로 이루어진다.

집계 : 순위 선택 투표가 완료된 후, 각 후보자 페어에 대해 어떤 후보자가 얼마 만큼의 득표차로 선호되었는지 집계한다.
정렬 : 승리의 강도에 따라 내림차순으로 후보자 페어를 정렬한다. 승리의 강도란 그 후보자를 선호한 투표자의 수를 의미한다.
고정 : 가장 강력한 페어의 화살표부터 그래프에 고정한다. 사이클이 생성되지 않도록 하나씩 순서대로 진행한다.

그래프가 완성되면, 그래프의 원천이 되는 후보자가 승자가 된다.

Tideman 과제

아래 예시와 같이 Tideman 시스템에 따라 동작하는 투표 프로그램을 작성한다.

./tideman Alice Bob Charlie
Number of voters: 5
Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob

Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob

Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice

Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice

Rank 1: Charlie
Rank 2: Alice
Rank 3: Bob

Charlie

과제용 뼈대 코드

int 타입의 2차원 preference 배열 : preferences[i][j]는 후보 i를 후보 j보다 선호하는 투표자의 수를 의미한다.
boolean 타입의 2차원 locked 배열 : locked[i][j]는 후보 i가 후보 j를 가리키는 화살표가 존재하는 것을 의미한다(인접 행렬).
pair 구조체 : 후보자 페어를 나타낸다. winner는 승자의 인덱스를, loser은 패자의 인덱스를 저장한다.
후보자의 이름은 string 타입의 candidates 배열에 저장되며, 각 페어에 대한 결과는 pairs 배열에 저장된다.
전역변수 pair_count 및 candidate_count : 각각 페어의 수와 후보자의 수를 저장한다.

Main()

candidate_count를 결정한 뒤, candidate_count만큼 루프를 돌아 locked의 각 원소를 false로 초기화한다. 즉 아직 고정된 화살표가 없다는 것을 의미한다.
그 다음 프로그램은 루프를 돌아 모든 투표자에게 선호 순위를 수집하여 ranks에 저장한다(vote 호출). ranks[i]는 한 투표자가 i번째로 선호하는 후보자의 인덱스를 의미한다. record_preference 함수는 ranks를 인수로 전달받아 전역 변수인 preferences를 업데이트 한다.
투표 집계가 완료되면, add_pairs를 호출하여 모든 후보자 페어를 pairs에 추가한 뒤 sort_pairs를 호출하여 정렬하고, lock_pairs를 통해 그래프를 완성한다. 마지막으로 print_winner를 호출하여 최종 승자의 이름을 출력한다.

지시사항

vote 함수를 완성한다.
- 함수는 rank, name, ranks를 인수로 받는다.
- name이 유효한 이름이면 ranks를 업데이트한다.
- ranks[i]는 투표자가 i번째 선호한 후보자를 의미한다.
- 함수는 순위가 성공적으로 저장된 경우 true를 반환하고, 그렇지 않다면 false를 반환한다(예를 들어 인수로 받은 name이 유효한 이름이 아닌 경우).
- 후보자의 이름은 중복되지 않는다고 가정한다.
record_preferences 함수를 완성한다.
- 각 투표자에 대해 한 번씩 호출되며, ranks를 인수로 받는다.
- 해당 투표자의 선호 순위에 맞게 전역변수 preferences를 업데이트한다. preferences[i][j]는 후보 i를 후보 j보다 선호하는 투표자의 수를 의미한다.
- 모든 투표자가 모든 후보자에 대한 순위를 정했다고 가정한다.
add_pairs 함수를 완성한다.
- pairs를 업데이트한다. 만약 페어가 동점인 경우에는 업데이트하지 않는다.
- 젼역번수 pair_count를 업데이트한다. 모든 페어는 pairs[0] ~ pairs[pair_count - 1] 범위에 저장된다.
sort_pairs 함수를 완성한다.
- 승리 강도에 따라 내림차순으로 pairs 배열을 정렬한다. 승리의 강도란 그 후보자를 선호한 투표자의 수를 의미한다. 만약 같은 강도를 가진 페어가 여러 개 있다면, 그 페어들은 정렬하지 않아도 된다.
lock_pairs 함수를 완성한다.
- 그래프를 완성한다. 승리 강도가 큰 순으로 화살표를 추가하고, 사이클을 만들지 않도록 한다.
print_winner 함수를 완성한다.
- 그래프의 원천이 되는 후보자의 이름을 출력한다. 복수의 원천은 없다고 가정한다.

제공된 소스코드에서 vote, record_preferences, add_pairs, sort_pairs, lock_pairs
, print_winner 함수 외에는 수정해서는 안된다. 단 헤더 파일이나 지시사항을 위반하지 않는 선에서의 다른 함수의 추가는 허용된다.

✍️ 풀이

vote()

bool vote(int rank, string name, int ranks[])
{
    for (int i = 0; i < candidate_count; i++)
    {
        if (strcmp(name, candidates[i]) == 0)
        {
            ranks[rank] = i;
            return true;
        }
    }

    return false;
}

사용자의 입력값인 name이 유효한 이름인지 체크하고, 유효하다면 ranks[]에 저장한다. 그렇지 않다면 false를 반환하고 main은 프로그램을 종료한다.

record_preferences()

void record_preferences(int ranks[])
{
    for (int i = 0; i < candidate_count - 1; i++)
    {
        for (int j = i + 1; j < candidate_count; j++)
        {
            preferences[ranks[i]][ranks[j]]++;
        }
    }

    return;
}

vote()에서 한 투표자의 선호 순위를 ranks[]에 저장
ranks[]를 인수로 받아 각 후보자 페어에 대한 결과를 preferences에 업데이트
- vote()의 결과로 ranks에 {0, 1, 2}가 저장된 경우, 1번째로 선호된 0번 후보는 2번째 선호된 1번 후보와의 대결에서 1표, 3번째 선호된 2번 후보의 대결에서 1표를 획득하고 이것은 preferences[0][1], preferences[0][2]에 각각 반영된다.

add_pairs()

void add_pairs(void)
{
    for (int i = 0; i < candidate_count - 1; i++)
    {
        for (int j = i + 1; j < candidate_count; j++)
        {
            if (preferences[i][j] > preferences[j][i])
            {
                pairs[pair_count].winner = i;
                pairs[pair_count].loser = j;
                pair_count++;
            }
            else if (preferences[i][j] < preferences[j][i])
            {
                pairs[pair_count].winner = j;
                pairs[pair_count].loser = i;
                pair_count++;
            }
        }
    }

    return;
}

{0, 1, 2, 3} 4명의 후보가 존재할 때 생성되는 페어 :

01 12 23
02 13
03

preferences를 완성한 후 pairs에 모든 페어를 저장한다. 동시에 전역변수 pair_count도 업데이트한다.
페어를 i - j 의 형태로 나타내면, i는 0번 인덱스부터 마지막에서 1 적은 인덱스까지, j는 1번 인덱스부터 마지막 인덱스까지 루프를 돌며 페어를 이룬다.

sort_pairs()

강의에서 배운 정렬 알고리즘은 버블 정렬, 선택 정렬, 합병 정렬이었고 그 중에서도 합병 정렬의 속도가 탁월하다고 했다. 하지만 합병 정렬을 쓰려면 sort_pairs()에 파라미터를 설정하는게 좋은데 이미 void로 선언되어 있어서 같은 분할 정복 정렬 중 하나인 qsort()를 선택했다.

void sort_pairs(void)
{
    qsort(pairs, pair_count, sizeof(pair), compare_pair);
    return;
}

qsort(정렬할 배열, 요소 개수, 요소 크기, 비교함수);
stdlib.h에 정의됨

int compare_pair(const void *a, const void *b)
{
    const pair *pa = (const pair *)a;
    const pair *pb = (const pair *)b;

    int margin_a = preferences[pa->winner][pa->loser] - preferences[pb->winner][pb->loser];
    int margin_b = preferences[pb->winner][pb->loser] - preferences[pa->winner][pa->loser];

    if (margin_a > margin_b)
    {
        return -1;
    }
    else if (margin_a < margin_b)
    {
        return 1;
    }
    else
    {
        return 0;
    }
}

void형 포인터 : 모든 자료형의 포인터를 저장할 수 있다. 컴파일 시에 포인터의 자료형을 결정할 수 없는 경우 사용된다.
포인터 형변환 : 포인터 변수는 자료형에 따라 메모리에서 값을 읽어오는 크기가 다르기 때문에 포인터 자료형이 존재한다. void형 포인터 변수는 주소를 저장할 뿐 그대로 사용할 수 없고, 자료형에 맞게 형변환을 해주어야 한다.
화살표 연산자 : 구조체 포인터의 멤버에 접근하기 위해서는 화살표 연산자(→)를 사용한다.
리턴 값 : 비교 함수의 리턴 값은 약속된 내용으로, margin_a > margin_b인 경우 리턴값이 음수(-1)인 것은 큰 값인 margin_a가 앞쪽에 정렬된다는 의미이다. 리턴 값이 꼭 -1, 0, 1일 필요는 없고 음수, 0, 양수이면 되기 때문에 아래의 코드도 결과는 같다.
```
return margin_b - margin_a;
```

lock_pairs()

void lock_pairs(void)
{
    for (int i = 0; i < pair_count; i++)
    {
        if (!cycle(pairs[i].winner, pairs[i].loser))
        {
            locked[pairs[i].winner][pairs[i].loser] = true;
        }
    }

    return;
}

pairs의 0번째 멤버부터 cycle()함수로 싸이클이 있는지 체크하고, 없다면 locked 변수를 업데이트 한다.

bool cycle(int start, int edge)
{

    if (start == edge)
    {
        return true;
    }

    for (int i = 0; i < candidate_count; i++)
    {
        if (locked[edge][i] == true)
        {
            if (cycle(start, i))
            {
                return true;
            }
        }
    }

    return false;
}

파라미터로 해당 페어의 승자 및 패자의 인덱스를 받는다. 그래프로 표현했을 때 0 → 1인 경우 start는 0, edge는 1이 된다.
재귀 함수를 통해 start인 0은 계속 가져가고, 반복문을 통해 locked에서 edge → i가 true인 페어를 찾는다. true인 페어가 존재한다면 i를 edge로 두고 다른 i를 반복하여 edge → i가 true인 페어가 존재하는지 검색을 반복한다.
start가 0이었다면, 이 과정을 반복하여 최종적으로 i → 0(start == edge)가 되는 경우 싸이클이 존재하는 것이므로 최종적으로 true를 반환한다. lock_pairs()는 cycle()에게 true를 받은 경우 해당 페어는 locked에 반영하지 않는다.
처음에는 싸이클은 0 → 1 → 2 → 0 또는 0 → 2 → 1 → 0처럼 1씩 증가하거나 감소하는 형태만 싸이클이라고 잘못 이해해서 check50을 통과하지 못했다. 하지만 싸이클은 어느 후보자도 원천이 되지 못하는 경우로, 0 → 1 → 3 → 2 → 0과 같은 경우도 싸이클에 해당한다.

print_winner()

void print_winner(void)
{
    for (int i = 0; i < candidate_count; i++)
    {
        int false_count = 0;

        for (int j = 0; j < candidate_count; j++)
        {
            if (locked[j][i] == false)
            {
                false_count++;
            }

            if (false_count == candidate_count)
            {
                printf("%s\n", candidates[i]);
            }
        }
    }

    return;
}

그래프의 원천이 된다는 것은 locked에서 true가 없는 경우, 즉 모두 false인 경우이다.
후보자 i의 locked 값을 검사하는 외부 반복문이 실행될 때마다 false_count를 0으로 초기화한다. 내부 반복문을 실행하여 i 후보자와 다른 각각의 후보자 j와의 그래프 관계를 검사한다. 화살표가 i를 가리키지 않는 경우(locked[i][j] == false) false_count를 1 증가시킨다. false_count가 candidate_count와 동일한 경우 그래프의 원천, 즉 승자를 의미하기 때문에 해당 후보자의 이름을 출력한다.

✍️ 메모

재귀함수와 반복문

강의에서는 Mario 과제(별찍기 문제와 유사)를 예를 들며 재귀함수를 이용하면 반복문을 쓰는 것보다 코드가 간결하고 보기 좋다고 했지만, 재귀함수가 익숙하지 않은 나에게는 정말 반복문보다 좋은 것이 맞나? 생각이 들었다.

비교를 위해 ChatGPT에게 cycle()함수를 재귀함수 대신 for 루프를 이용한 반복문으로 바꿔달라고 요청했다.

bool cycle(int start, int edge)
{
    // Create a stack to keep track of nodes to visit
    int stack[MAX];
    int top = -1;

    // Create a boolean array to track visited nodes
    bool visited[candidate_count];
    for (int i = 0; i < candidate_count; i++)
    {
        visited[i] = false;
    }

    // Push the edge node onto the stack
    stack[++top] = edge;

    // Loop through all nodes in the stack
    while (top >= 0)
    {
        // Pop the top node from the stack
        int node = stack[top--];

        // Check if the node has been visited before
        if (visited[node])
        {
            continue;
        }

        // Mark the node as visited
        visited[node] = true;

        // Check if the node is the start node
        if (node == start)
        {
            return true;
        }

        // Push all nodes that are locked over the current node onto the stack
        for (int i = 0; i < candidate_count; i++)
        {
            if (locked[node][i])
            {
                stack[++top] = i;
            }
        }
    }

    // If no cycles are found, return false
    return false;
}

과제 체크 프로그램인 check50에 넣어보니 통과한다.

코드가 복잡해졌다. 재귀함수에서는 조건문이 true인 경우 그 안에서 다시 자신을 호출함으로써 재귀함수끼리 연결되어있기 때문에 진행 상태를 별도의 변수에 저장할 필요가 없었다. 하지만 반복문을 사용하니 stack, top, visited 변수가 추가되었고 while 루프 제어를 위한 조건문도 추가되었다.

반복문이 시간 및 공간 효율이 더 좋기 때문에 대부분의 경우에는 반복문을 사용하는 것이 좋고, 재귀함수는 피보나치 수열이나 팩토리얼처럼 작고 비슷한 문제들을 해결하는 방식에 의존하는 경우에 유용하다고 한다.

fibonacci(n) = fibonacci(n-1) + fibonacci(n-2)
factorial(n) = n * factorial(n-1)

재귀함수는 트리나 그래프에 대한 작업에도 유용한데, cycle()도 트리 순회 알고리즘이라는 것 같다. 이번 과제에서는 여기까지만 알아보고 알고리즘을 공부하고 다시 보는게 좋을 것 같다.

마감 기한

lock_pairs()와 cycle()에서 막히는 바람에 계획했던 일정을 넘겨버렸다. 너무 안 풀리니까 집중이 안돼서 버린 시간도 많았다. 꼭 내 힘으로 풀어야지! 하는 마음이었는데, 별로 좋은 공부 전략은 아닌 것 같다. 너무 쉽게 포기해도 문제겠지만 현재 나의 실력으로는 어렵다는 것을 빨리 깨닫는 것도 중요한 것 같다.

다음부터는 한 섹션에 1주일만 할당하고 풀리지 않으면 적당한 선에서 마무리 하고 솔루션을 찾아봐야겠다.

References

CS50 Fall 2019 Problem set 3 Tideman
"50.2 퀵 정렬 함수 사용하기" 코딩 도장. Accessed: February 13, 2023. https://dojang.io/mod/page/view.php?id=2028.
"C 언어 포인터 변수 자료형이 필요한 이유" Programist's Laboratory. Accessed: February 14, 2023. https://programist.tistory.com/entry/C-언어-포인터-변수-자료형이-필요한-이유.
"CS50 PSet3: Tideman" Medium. Accessed: February 14, 2023. https://joseph28robinson.medium.com/cs50-pset3-tideman-87f22f0f0bc3.
"Difference between Recursion and Iteration" GeeksforGeeks. Accessed: February 14, 2023. https://www.geeksforgeeks.org/difference-between-recursion-and-iteration/.
"Difference Between Recursion and Iteration" Interview Kickstart. Accessed: February 14, 2023. https://www.interviewkickstart.com/learn/difference-between-recursion-and-iteration.

dondonee

이전 포스트

CS50 Probelm set 3 - 결선 투표

다음 포스트