개요
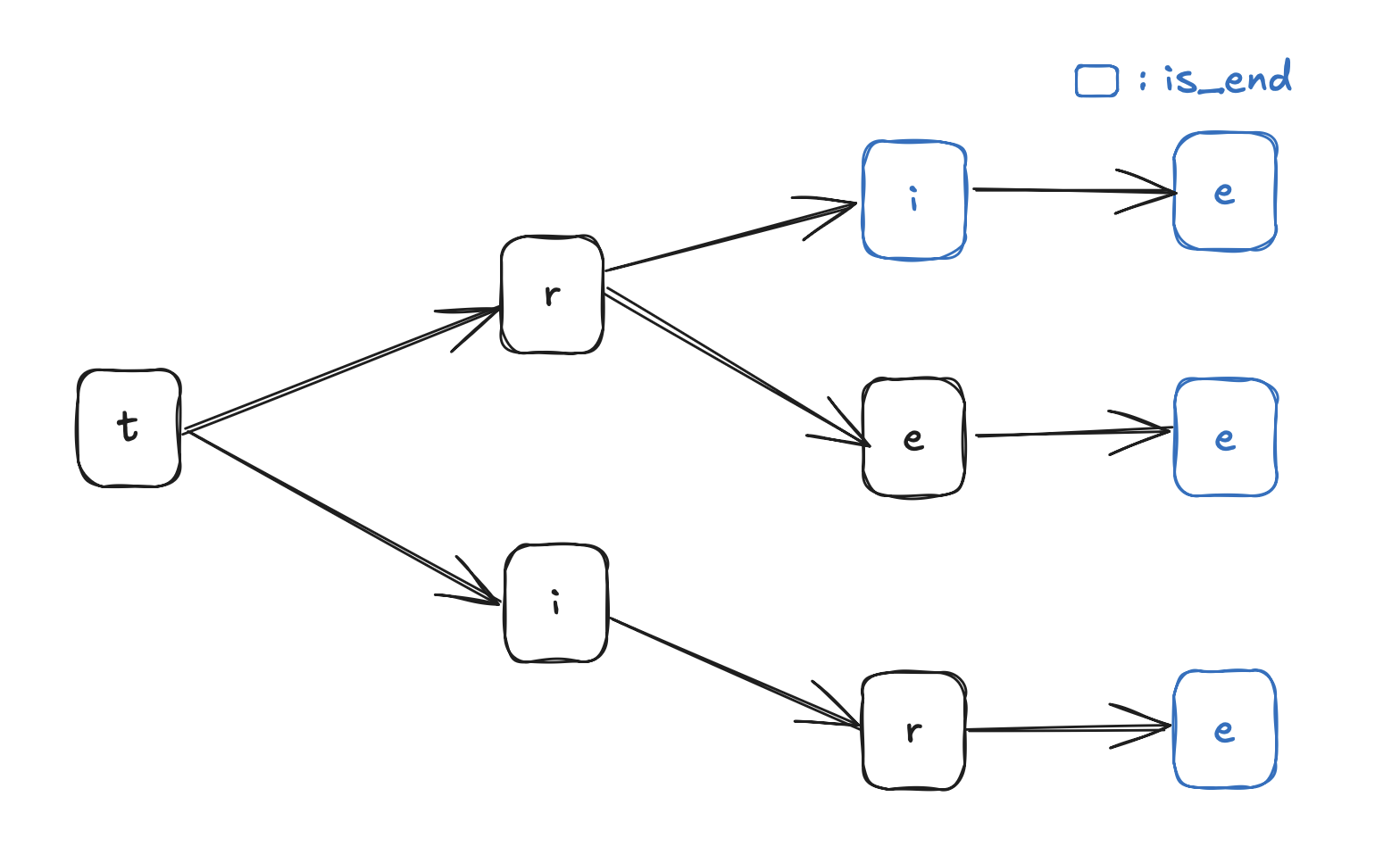
트라이는 문자열 탐색을 위해 주로 사용되는 트리 구조입니다.
철자를 나눠 저장함으로써 빠른 검색과 공간 효율성이 높은 구조로, 검색어 추천 등 다양하게 사용될 수 있습니다.
구현방식
이를 구현하기 위해 Python에서 위와 같은 방식으로 클래스를 만들어 구현하는 경우가 많은데, 클래스 구현이 어렵거나 익숙하지 않은 사람들을 위해서 간단한 구현 방법을 같이 설명해보려고 합니다.
일반적인 트리도 파이썬에서 리스트와 인덱스 기반으로 구현하듯이, 트라이도 딕셔너리를 기반으로 간단하게 구현할 수 있습니다.
1. 클래스를 통한 구현
Class Node:
def __init__(self,data):
self.data = data
self.child = dict()
self.is_end = False
Class Trie:
def __init__(self):
self.root = Node("")
def insert(self, word):
now = self.root
for char in word:
if char not in now.child:
now.child[char] = Node(char)
now = now.child[char]
now.is_end = True
def find(self, word):
now = self.root
for char in word:
if char not in now.child:
return False
now = now.child[char]
if now.is_end:
return True
return False
2. 딕셔너리를 통한 구현
def insert(word):
now = trie
for char in word:
now = now.setdefault(char, dict())
now["is_end"] = True
def find(word):
now = trie
for char in word:
if char not in now:
return False
now = now[char]
if "is_end" in now:
return True
return False
trie = dict()
insert("trie")
insert("tri")
insert("tire")
insert("tree")
print(find("tree")) # True
print(find("tre")) # False
print(trie)
'''
{
"t": {
"i": {
"r": {
"e": {
"is_end": True
}
}
},
"r": {
"i": {
"is_end": True,
"e": {
"is_end": True
}
},
"e": {
"e": {
"is_end": True
}
}
}
}
}
'''
트라이에 문자열을 입력하고, 찾는 함수를 위와 같이 짧은 함수로 구현할 수 있습니다.
이후, 추가적인 메서드들의 구현 또한 딕셔너리를 기반으로 생각해서 구현하면 편합니다.
그리고 딕셔너리를 기반으로 구현하는 경우, Node 와 같은 자체 구현 클래스와 다르게 pprint를 통해 시각적으로 확인하기 편하다는 점 또한 장점입니다.
아래에는 간단한 트라이 문제들을 이러한 방식으로 구현하여 풀이한 것을 소개합니다.
관련 문제
[백준/python] 14725 개미굴
[백준/python] 16934 게임 닉네임
[백준/python] 9202 Boggle
[백준/python] 5670 휴대폰 자판
[백준/python] 13505 두 수 XOR
